Классификация фазовых переходов

При фазовом переходе первого рода скачкообразно изменяются самые главные, первичные экстенсивные параметры: удельный объём, количество запасённой внутренней энергии, концентрация компонентов и т. п. Подчеркнём: имеется в виду скачкообразное изменение этих величин при изменении температуры, давления и т. п., а не скачкообразное изменение во времени (насчёт последнего см. ниже раздел Динамика фазовых переходов).

Наиболее распространённые примеры фазовых переходов первого рода:

• плавление и кристаллизация

• испарение и конденсация

• сублимация и десублимация

При фазовом переходе второго рода плотность и внутренняя энергия не меняются, так что невооружённым глазом такой фазовый переход может быть незаметен. Скачок же испытывают их производные по температуре и давлению: теплоёмкость, коэффициент теплового расширения, различные восприимчивости и т. д.

Фазовые переходы второго рода происходят в тех случаях, когда меняется симметрия строения вещества (симметрия может полностью исчезнуть или понизиться). Описание фазового перехода второго рода как следствие изменения симметрии даётся теорией Ландау. В настоящее время принято говорить не об изменении симметрии, но о появлении в точке перехода параметра порядка, равного нулю в менее упорядоченной фазе и изменяющегося от нуля (в точке перехода) до ненулевых значений в более упорядоченной фазе.

Наиболее распространённые примеры фазовых переходов второго рода:

• прохождение системы через критическую точку

• переход парамагнетик-ферромагнетик или парамагнетик-антиферромагнетик (параметр порядка — намагниченность)

• переход металлов и сплавов в состояние сверхпроводимости (параметр порядка — плотность сверхпроводящего конденсата)

• переход жидкого гелия в сверхтекучее состояние (п.п. — плотность сверхтекучей компоненты)

• переход аморфных материалов в стеклообразное состояние

Современная физика исследует также системы, обладающие фазовыми переходами третьего или более высокого рода.

В последнее время широкое распространение получило понятие квантовый фазовый переход, т.е. фазовый переход, управляемый не классическими тепловыми флуктуациями, а квантовыми, которые существуют даже при абсолютном нуле температур, где классический фазовый переход не может реализоваться вследствие теоремы Нернста.

Динамика фазовых переходов

Как сказано выше, под скачкообразным изменением свойств вещества имеется в виду скачок при изменении температуры и давления. В реальности же, воздействуя на систему, мы изменяем не эти величины, а её объем и её полную внутреннюю энергию. Это изменение всегда происходит с какой-то конечной скоростью, а значит, что для того, чтобы «покрыть» весь разрыв в плотности или удельной внутренней энергии, нам требуется некоторое конечное время. В течение этого времени фазовый переход происходит не сразу во всём объёме вещества, а постепенно. При этом в случае фазового перехода первого рода выделяется (или забирается) определённое количество энергии, которая называется теплотой фазового перехода. Для того, чтобы фазовый переход не останавливался, требуется непрерывно отводить (или подводить) это тепло, либо компенсировать его совершением работы над системой.

В результате, в течение этого времени точка на фазовой диаграмме, описывающая систему, «замирает» (т.е. давление и температура остаются постоянными) до полного завершения процесса.

Тройна́я то́чка — точка на фазовой диаграмме, где сходятся три линии фазовых переходов. Тройная точка — это одна из характеристик химического вещества. Обычно тройная точка определяется значением температуры и давления, при котором вещество может равновесно находиться в трёх (отсюда и название) агрегатных состояниях — твёрдом, жидком и газообразном. В этой точке сходятся линии плавления, кипения и сублимации.

В более общем случае могут рассматриваться и другие фазы вещества, не соответствующие различным агрегатным состояниям. На достаточно богатых фазовых диаграммах может быть несколько тройных точек. Вещество в тройной точке в состоянии термодинамического равновесия может частично находиться во всех трёх фазах. На многомерных фазовых диаграммах (то есть если кроме температуры и давления присутствуют иные интенсивные величины) могут существовать четверные и т. д. точки.

24. Наиболее характерным свойством жидкости, отличающим ее от газа, является то, что на границе с газом жидкость образует свободную поверхность, наличие которой приводит к возникновению явлений особого рода, называемых поверхностными. Своим возникновением они обязаны особым физическим условиям, в которых находятся молекулы вблизи свободной поверхности.

На каждую молекулу жидкости действуют силы притяжения со стороны окружающих ее молекул, расположенных от нее на расстоянии порядка 10^-9 м (радиус молекулярного действия). На молекулу M₁, расположенную внутри жидкости (рис. 1), действуют силы со стороны таких же молекул, и равнодействующая этих сил близка к нулю.

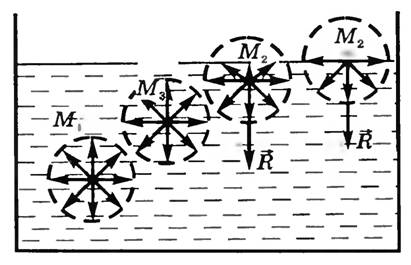
Рис. 1

Для молекул M₂ равнодействующие сил отличны от нуля и направлены внутрь жидкости, перпендикулярно к ее поверхности. Таким образом, все молекулы жидкости, находящиеся в поверхностном слое, втягиваются внутрь жидкости. Но пространство внутри жидкости занято другими молекулами, поэтому поверхностный слой создает давление на жидкость (молекулярное давление).

Чтобы переместить молекулу M₃, расположенную непосредственно под поверхностным слоем, на поверхность, необходимо совершить работу против сил молекулярного давления. Следовательно, молекулы поверхностного слоя жидкости обладают дополнительной потенциальной энергией по сравнению с молекулами внутри жидкости. Эту энергию называют поверхностной энергией.

Очевидно, что величина поверхностной энергии тем больше, чем больше площадь свободной поверхности.

Пусть площадь свободной поверхности изменилась на ΔS, при этом поверхностная энергия изменилась на  ΔWp=αΔS, где α — коэффициент поверхностного натяжения.

Так как для этого изменения необходимо совершить работу

 A=ΔWp, то  A=α⋅ΔS.

Отсюда  α=AΔS .

Единицей коэффициента поверхностного натяжения в СИ является джоуль на квадратный метр (Дж/м²).

Коэффициент поверхностного натяжения — величина, численно равная работе, совершенной молекулярными силами при изменении площади свободной поверхности жидкости на единицу при изотермическом процессе.

Так как любая система, предоставленная сама себе, стремится занять такое положение, в котором ее потенциальная энергия наименьшая, то жидкость обнаруживает стремление к сокращению свободной поверхности.

Поверхностный слой жидкости ведет себя подобно растянутой резиновой пленке, т.е. все время стремится сократить площадь своей поверхности до минимальных размеров, возможных при данном объеме.

Пример: капля жидкости в состоянии невесомости имеет сферическую форму.