Кпд тепловой машины Карно

Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно

.

Аналогично, при изотермическом сжатии рабочее тело отдало холодильнику

.

Отсюда коэффициент полезного действия тепловой машины Карно равен

.

Из последнего выражения видно, что КПД тепловой машины Карно зависит только от температур нагревателя и холодильника. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.

Поэтому максимальный КПД любой тепловой машины будет меньше или равен КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника. Например, КПД идеального цикла Стирлинга равен КПД цикла Карно.

Связь между обратимостью цикла и кпд

Для того, чтобы цикл был обратимым, из него должна быть исключена передача теплоты при наличии разности температур (так как такие процессы необратимы в силу постулата Томсона). Значит, передача теплоты должна осуществляться либо в изотермическом процессе (как в цикле Карно), либо в эквидистантном процессе (обобщённый цикл Карно или, для примера, его частный случай Цикл Брайтона). Для того, чтобы менять температуру рабочего тела от температуры нагревателя до температуры холодильника и обратно, необходимо использовать либо адиабатические процессы (они идут без теплообмена и, значит, не влияют на энтропию), либо циклы с регенерацией тепла при которых нет передачи тепла при разности температур. Мы приходим к выводу, что любой обратимый цикл может быть сведён к циклу Карно.

Примером обратимого цикла, не являющегося циклом Карно, но интегрально совпадающим с ним, является идеальный цикл Стирлинга: в двигателе Стирлинга добавлен регенератор, обеспечивающий полное приближение цикла к циклу Карно с достижением обратимости и тех же величин КПД.

Если же в цикле возникает передача теплоты при наличии разности температур, а таковыми являются все технические реализации термодинамических циклов, то цикл утрачивает свойство обратимости. Иначе говоря, посредством отведённой в цикле механической работы становится невозможным получить исходную теплоту. КПД такого цикла будет всегда меньше чем КПД цикла Карно.

22. Межмолекулярное взаимодействие — взаимодействие между электрически нейтральными молекулами или атомами. Впервые были учтены Я. Д. Ван-дер-Ваальсом в 1873 году. Учёт межмолекулярных сил необходим для объяснения свойств реальных газов и жидкостей.

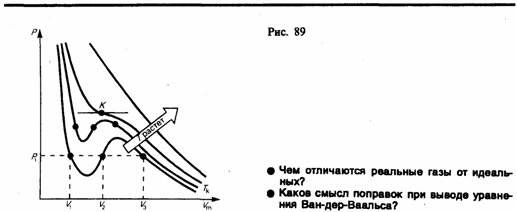
Для исследования поведения реального газа рассмотрим изотермы Ван-дер-Ваальса — кривые зависимости р от V_m при заданных Т, определяемые уравнением Ван-дер-Ваальса (61.2) для моля газа. Эти кривые (рассматриваются для четырех различных температур; рис. 89) имеют довольно своеобразный характер. При высоких температурах (T > T_к) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кри­вой. При некоторой температуре T_к на изотерме имеется лишь одна точка перегиба К.

Эта изотерма называется критической, соответствующая ей температура T_к — крити­ческой температурой; точка перегиба К называется критической точкой; в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке объем V_к, и давление р_к называются также критическими. Состояние с критическими парамет­рами (p_к, V_к, T_к) называется критическим состоянием. При низких температурах (Т < T_к ) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь.

Для пояснения характера изотерм преобразуем уравнение Ван-дер-Ваальса (61.2) к виду

                               (62.1)

Уравнение (62.1) при заданных р и Т является уравнением третьей степени от­носительно V_m; следовательно, оно может иметь либо три вещественных корня, либо один вещественный и два мнимых, причем физический смысл имеют лишь веществен­ные положительные корни. Поэтому первому случаю соответствуют изотермы при низких температурах (три значения объема газа V₁, V₂ и V₃ отвечают (символ «m» для простоты опускаем) одному значению давления р₁), второму случаю — изотермы при высоких температурах.

Рассматривая различные участки изотермы при T<Т_к (рис. 90), видим, что на участках 1—3 и 5—7 при уменьшении объема V_m давление р возрастает, что естествен­но. На участке 3—5 сжатие вещества приводит к уменьшению давления; практика же показывает, что такие состояния в природе не осуществляются. Наличие участка 3—5 означает, что при постепенном изменении объема вещество не может оставаться все время в виде однородной среды; в некоторый момент должно наступить скачкообразное изменение состояния и распад вещества на две фазы. Таким образом, истинная изотерма будет иметь вид ломаной линии 7—6—2—1. Часть 6–7 отвечает газообраз­ному состоянию, а часть 2–1 — жидкому. В состояниях, соответствующих горизон­тальному участку изотермы 6—2, наблюдается равновесие жидкой и газообразной фаз вещества. Вещество в газообразном состоянии при температуре ниже критической называется паром, а пар, находящийся в равновесии со своей жидкостью, называется насыщенным.