
- •3. Основная задача динамики
- •9. Кинетическая и потенциальная энергия
- •Сохранение механической энергии
- •11. Уравнение неразрывности
- •Уравнение Бернулли
- •Закон Стокса
- •Вывод уравнения
- •Показатель адиабаты
- •Кпд тепловой машины Карно
- •Связь между обратимостью цикла и кпд
- •Уравнение состояния
- •Условие равновесия фаз
- •Уравнение Клапейрона — Клаузиуса
- •Классификация фазовых переходов
- •Динамика фазовых переходов
- •Формула Лапласа
Закон Стокса
Линии обтекающего потока, лобовое сопротивление Fd, сила тяжести Fg.
В 1851 Джордж Стокс получил выражение для силы трения (также называемой силой лобового сопротивления), действующей на сферические объекты с очень маленькими числами Рейнольдса (например, очень маленькие частицы) в непрерывной вязкой жидкости, решая уравнение Навье — Стокса:
![]()
где
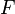 —
сила трения, так же называемая силой
Стокса,
—
сила трения, так же называемая силой
Стокса, —
радиус сферического объекта,
—
радиус сферического объекта,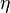 —
динамическая
вязкость жидкости,
—
динамическая
вязкость жидкости,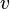 —
скорость частицы.
—
скорость частицы.
Если частицы падают в вязкой жидкости под действием собственного веса, то установившаяся скорость достигается, когда эта сила трения совместно с силой Архимеда точно уравновешиваются силой гравитации. Результирующая скорость равна
![]()
где
Vs — установившаяся скорость частицы (м/с) (частица движется вниз если
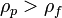 ,
и вверх в случае
,
и вверх в случае
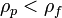 ),
),— радиус Стокса частицы (м),
g — ускорение свободного падения (м/с²),
ρp — плотность частиц (кг/м³),
ρf — плотность жидкости (кг/м³),
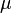 —
динамическая вязкость
жидкости (Па с).
—
динамическая вязкость
жидкости (Па с).
13. Статический метод исследования - это метод, который интересуется не движением отдельных молекул, а лишь такими средними величинами, которые характеризуют движение огромной совокупности частиц (статическая физика). Термодинамический метод исследования - это метод исследования различных свойств тел и изменения состояния вещества (изучение микроскопических свойств тел и явлений природы).Термодинамические параметры. При указании состояния газа используются различные термодинамические параметры : это p - давление, V - объём и T - температура. Между ними существует связь, которая может быть заданна в виде функции F(p,V,T)=0. Нормальные условия T=273, p=105Па, Vм=22,4 10-3м3/моль (Vм - объём одного моля газа). Равновесные и неравновесные состояния и процессы. Всякая система может находиться в разных состояниях, отличается температурой, давлением и объёмом - это термодинамические параметры. Состояния бывают равновесными и неравновесными. Равновесные состояния - это состояния, при которых все параметры системы имеют определённые значения, остающиеся при неизменных условиях одинаковыми. Неравновесные состояния - это состояния, при которых какой-нибудь параметр изменяется. Процесс - это переход системы из одного состояния в другое. Равномерный процесс - это процесс состоящий из непрерывных состояний. Уравнение состояния идеального газа (уравнение Менделеева-Клаперон) pV=(m/M)RT, где m-это масса газа, M - молярная масса, m/M= - количество вещества.
14.
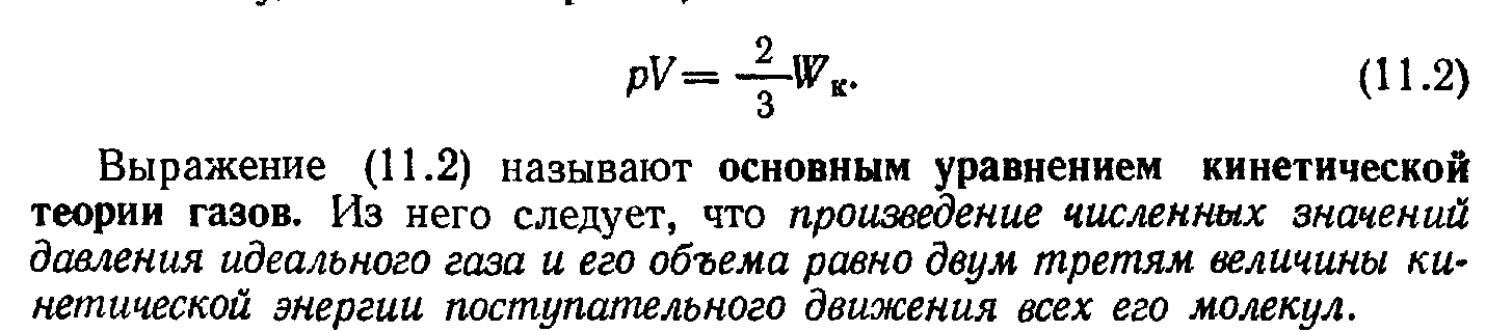
|
Сравнивая уравнение состояния идеального газа и основное уравнение кинетической теории газов, записанные для одного моля (для этого число молекул N возьмём равным числу Авогадро NА), найдём среднюю кинетическую энергию одной молекулы:
Откуда
Средняя кинетическая энергия поступательного движения молекулы не зависит от её природы и пропорциональна абсолютной температуре газа T. Отсюда следует, что абсолютная температура является мерой средней кинетической энергии молекул. |
Молекулярно- кинетическое толкование абсолютной температуры:
Абсолютная температура – есть величина, пропорциональная средней энергии поступательного движения молекул.
15.
При
выводе основного уравнения
молекулярно-кинетической теории
полагалось, что молекулы имеют различные
скорости. После многократных соударений
скорость каждой молекулы изменяется
по модулю и направлению. Но из-за
хаотического движения молекул все
направления движения равновероятны,
т. е. в любом направлении в среднем
движется равное число молекул.
Согласно
молекулярно-кинетической теории, как
бы ни изменялись при столкновениях
скорости молекул, средняя квадратичная
скорость молекул массой m0
в газе, который находится в состоянии
равновесия при Т= const, остается неизменно
и равной
Это объясняется тем, что
в газе, находящемся в состоянии равновесия,
устанавливается некоторое стационарное,
не меняющееся со временем статистическое
распределение молекул по скоростям,
подчиняющаяся вполне определенному
статистическому закону. Этот закон
теоретически выведен Дж. Максвеллом.
При выводе закона распределения
молекул по скоростям Максвелл сделал
предположение, что газ состоит из
огромного числа N тождественных молекул,
которые находятся в состоянии
беспорядочного теплового движения при
одинаковой температуре. Также
предполагалось, что силовые поля на газ
не действуют.
Закон Максвелла
описывается некоторой функцией f(ν),
которая называется функцией
распределения молекул по скоростям.
Если разбить диапазон скоростей молекул
на малые интервалы, которые равны dν, то
на каждый интервал скорости приходится
число молекул dN(ν),
имеющих скорость, которая заключена в
этом интервале. Функция f(ν)
задает относительное число молекул
dN(ν)/N,
скорости которых находятся в интервале
от ν
до ν+dν,
т. е.
![]() откуда
откуда
![]() Применяя
методы теории вероятностей, Максвелл
получил функцию f(ν)
— закон
о распределеня молекул идеального газа
по скоростям:
Применяя
методы теории вероятностей, Максвелл
получил функцию f(ν)
— закон
о распределеня молекул идеального газа
по скоростям:
![]() (1)
Из (1) видно, что конкретный вид
функции зависит от вида газа (от массы
молекулы) и от параметра состояния (от
температуры Т).
График функции
(1) приведен на рис. 1. Так как при возрастании
ν
множитель exp[–m0ν2/(2kT)]
уменьшается быстрее, чем увеличивается
множитель ν2,
то функция f(ν),
начинаясь от нуля, достигает максимума
при νB,
и затем асимптотически стремится к
нулю. Кривая несимметрична относительно
νB.
(1)
Из (1) видно, что конкретный вид
функции зависит от вида газа (от массы
молекулы) и от параметра состояния (от
температуры Т).
График функции
(1) приведен на рис. 1. Так как при возрастании
ν
множитель exp[–m0ν2/(2kT)]
уменьшается быстрее, чем увеличивается
множитель ν2,
то функция f(ν),
начинаясь от нуля, достигает максимума
при νB,
и затем асимптотически стремится к
нулю. Кривая несимметрична относительно
νB.
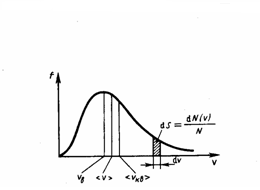
Рис.1
Относительное
число молекул dN(ν)/N,
со скоростями, лежащими в интервале от
ν
до ν+dν,
рассчитывается как площадь заштрихованной
полоски на рис. 1. Площадь, которая
ограничена кривой распределения и осью
абсцисс, равна единице. Это значит, что
функция f(ν)
удовлетворяет условию нормировки
![]() Скорость,
при которой максимальна функция
распределения молекул идеального газа
по скоростям, называется наиболее
вероятной скоростью,
значение которой можно найти
продифференцировав выражение (1)
(постоянные множители опускаем) по
аргументу ν,
при этом приравняв результат нулю и
используя условие для максимума выражения
f(ν):
Скорость,
при которой максимальна функция
распределения молекул идеального газа
по скоростям, называется наиболее
вероятной скоростью,
значение которой можно найти
продифференцировав выражение (1)
(постоянные множители опускаем) по
аргументу ν,
при этом приравняв результат нулю и
используя условие для максимума выражения
f(ν):
![]()
![]() Значения
ν=0
и ν=∞
соответствуют минимумам выражения (1),
а значение ν,
при котором выражение в скобках становится
равным нулю, и есть искомая наиболее
вероятная скорость νB:
Значения
ν=0
и ν=∞
соответствуют минимумам выражения (1),
а значение ν,
при котором выражение в скобках становится
равным нулю, и есть искомая наиболее
вероятная скорость νB:
![]() (2)
Из формулы (2) мы видим, что при
возрастании температуры максимум
функции распределения молекул по
скоростям (рис. 2) движется вправо (при
этом становится больше значение наиболее
вероятной скорости). Однако площадь,
которая ограничена кривой, не меняется,
поэтому кривая распределения молекул
по скоростям при повышении температуры
будет растягиваться и понижаться.
(2)
Из формулы (2) мы видим, что при
возрастании температуры максимум
функции распределения молекул по
скоростям (рис. 2) движется вправо (при
этом становится больше значение наиболее
вероятной скорости). Однако площадь,
которая ограничена кривой, не меняется,
поэтому кривая распределения молекул
по скоростям при повышении температуры
будет растягиваться и понижаться.
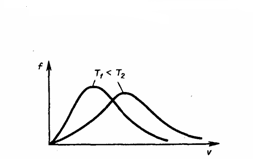
Рис.2
Средняя
скорость молекулы
<ν>
(средняя арифметическая скорость)
определяется по формуле
![]() Подставляя
сюда f(ν)
и интегрируя, получаем
Подставляя
сюда f(ν)
и интегрируя, получаем
![]() (3)
Скорости, которые характеризуют
состояние газа: 1) наиболее вероятная
(3)
Скорости, которые характеризуют
состояние газа: 1) наиболее вероятная
![]() 2)
средняя
2)
средняя
![]() 3)
средняя квадратичная
3)
средняя квадратичная
![]() (рис.
1). Исходя из распределения молекул по
скоростям
(рис.
1). Исходя из распределения молекул по
скоростям
![]() (4)
найдем распределение молекул
газа по значениям кинетической энергии
ε. С этой целью перейдем от переменной
ν
к переменной ε=m0v2/2.
Подставив в (4)
(4)
найдем распределение молекул
газа по значениям кинетической энергии
ε. С этой целью перейдем от переменной
ν
к переменной ε=m0v2/2.
Подставив в (4)
![]() и
и
![]() ,
получим
,
получим
![]() где
dN(ε) — число молекул, которые имели
кинетическую энергию поступательного
движения, заключенную в интервале от ε
до ε + dε.
Значит, функция
распределения молекул по энергиям
теплового движения
где
dN(ε) — число молекул, которые имели
кинетическую энергию поступательного
движения, заключенную в интервале от ε
до ε + dε.
Значит, функция
распределения молекул по энергиям
теплового движения
![]() Средняя
кинетическая энергия <ε> молекулы
идеального газа
Средняя
кинетическая энергия <ε> молекулы
идеального газа
![]() т.
е. получили результат, совпадающий с
формулой о средней кинетической энергии
движения одной молекулы идеального
газа, выводимой из молекулярно-кинетической
теории.
т.
е. получили результат, совпадающий с
формулой о средней кинетической энергии
движения одной молекулы идеального
газа, выводимой из молекулярно-кинетической
теории.
16. При рассмотрении кинетической теории газов и закона распределения Максвелла предполагалось, что на молекулы газа не действуют никакие силы, за исключением ударов молекул. Поэтому, молекулы равномерно распределяются по всему сосуду. В действительности молекулы любого газа всегда находятся в поле тяготения Земли. Вследствие этого, каждая молекула массой m испытывает действие силы тяжести f =mg.
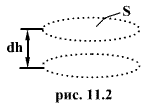
Выделим
горизонтальный элемент объема газа
высотой dh и площадью основания S (рис.
11.2). Считаем газ однородным и температуру
его постоянной. Число молекул в этом
объеме равно произведению его объема
dV=Sdh на число молекул
![]() в
единице объема. Полный вес молекул в
выделенном элементе равен
в
единице объема. Полный вес молекул в
выделенном элементе равен
![]()
Действие веса dF вызывает давление, равное
|
(11.2) |
минус - т.к. при увеличении dh давление уменьшается. Согласно основному уравнению молекулярно-кинетической теории
|
(11.3) |
Приравнивая правые части (11.2) и (11.3), получаем
![]() или
или
![]()
Интегрируя
это выражение в пределах от
![]() до
h (соответственно концентрация изменяется
от
до
n):
до
h (соответственно концентрация изменяется
от
до
n):
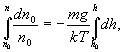 получим
получим
![]()
Потенцируя полученное выражение, находим
|
(11.4) |
Показатель
степени при exp имеет множитель
![]() ,
который определяет приращение
потенциальной энергии молекул газа.
Если переместить молекулу с уровня
до
уровня h, то изменение ее потенциальной
энергии будет
,
который определяет приращение
потенциальной энергии молекул газа.
Если переместить молекулу с уровня
до
уровня h, то изменение ее потенциальной
энергии будет
![]()
Тогда уравнение для концентрации молекул преобразуется к виду
|
(11.5) |
Это уравнение отображает общий закон Больцмана и дает распределение числа частиц в зависимости от их потенциальной энергии. Он применим к любой системе частиц, находящихся в силовом поле, например в электрическом.
Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести.
Для
идеального
газа, имеющего постоянную
температуру
![]() и
находящегося в однородном поле тяжести
(во всех точках его объёма ускорение
свободного падения
и
находящегося в однородном поле тяжести
(во всех точках его объёма ускорение
свободного падения
![]() одинаково),
барометрическая формула имеет следующий
вид:
одинаково),
барометрическая формула имеет следующий
вид:
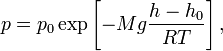
где
![]() —
давление газа в слое, расположенном на
высоте
—
давление газа в слое, расположенном на
высоте
![]() ,
,
![]() —
давление на нулевом уровне (
—
давление на нулевом уровне (![]() ),
),
![]() —
молярная
масса газа,
—
молярная
масса газа,
![]() —
газовая
постоянная,
—
абсолютная
температура. Из барометрической
формулы следует, что концентрация
молекул
—
газовая
постоянная,
—
абсолютная
температура. Из барометрической
формулы следует, что концентрация
молекул
![]() (или
плотность газа) убывает с высотой по
тому же закону:
(или
плотность газа) убывает с высотой по
тому же закону:
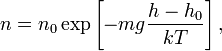
где
![]() —
масса молекулы газа,
—
масса молекулы газа,
![]() —
постоянная
Больцмана.
—
постоянная
Больцмана.
Барометрическая формула может быть получена из закона распределения молекул идеального газа по скоростям и координатам в потенциальном силовом поле (см. Статистика Максвелла — Больцмана). При этом должны выполняться два условия: постоянство температуры газа и однородность силового поля. Аналогичные условия могут выполняться и для мельчайших твёрдых частичек, взвешенных в жидкости или газе. Основываясь на этом, французский физик Ж. Перрен в 1908 году применил барометрическую формулу к распределению по высоте частичек эмульсии, что позволило ему непосредственно определить значение постоянной Больцмана.
Барометрическая
формула показывает, что плотность газа
уменьшается с высотой по экспоненциальному
закону. Величина
![]() ,
определяющая быстроту спада плотности,
представляет собой отношение потенциальной
энергии частиц к их средней кинетической
энергии, пропорциональной
,
определяющая быстроту спада плотности,
представляет собой отношение потенциальной
энергии частиц к их средней кинетической
энергии, пропорциональной
![]() .
Чем выше температура
,
тем медленнее убывает плотность с
высотой. С другой стороны, возрастание
силы тяжести
.
Чем выше температура
,
тем медленнее убывает плотность с
высотой. С другой стороны, возрастание
силы тяжести
![]() (при
неизменной температуре) приводит к
значительно большему уплотнению нижних
слоев и увеличению перепада (градиента)
плотности. Действующая на частицы сила
тяжести
может
изменяться за счёт двух величин: ускорения
и
массы частиц
.
(при
неизменной температуре) приводит к
значительно большему уплотнению нижних
слоев и увеличению перепада (градиента)
плотности. Действующая на частицы сила
тяжести
может
изменяться за счёт двух величин: ускорения
и
массы частиц
.
Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте.
Реальное распределение давления и плотности воздуха в земной атмосфере не следует барометрической формуле, так как в пределах атмосферы температура и ускорение свободного падения меняются с высотой и географической широтой. Кроме того, атмосферное давление увеличивается с концентрацией в атмосфере паров воды.
Барометрическая
формула лежит в основе барометрического
нивелирования — метода
определения разности высот
![]() между
двумя точками по измеряемому в этих
точках давлению (
между
двумя точками по измеряемому в этих
точках давлению (![]() и
и
![]() ).
Поскольку атмосферное давление зависит
от погоды, интервал времени между
измерениями должен быть возможно
меньшим, а пункты измерения располагаться
не слишком далеко друг от друга.
Барометрическая формула записывается
в этом случае в виде:
).
Поскольку атмосферное давление зависит
от погоды, интервал времени между
измерениями должен быть возможно
меньшим, а пункты измерения располагаться
не слишком далеко друг от друга.
Барометрическая формула записывается
в этом случае в виде:
![]() (в
м), где
(в
м), где
![]() —
средняя температура слоя воздуха между
точками измерения,
—
средняя температура слоя воздуха между
точками измерения,
![]() —
температурный коэффициент объёмного
расширения воздуха. Погрешность при
расчётах по этой формуле не превышает
0,1—0,5 % от измеряемой высоты. Более
точна формула Лапласа, учитывающая
влияние влажности воздуха и изменение
ускорения свободного падения.
—
температурный коэффициент объёмного
расширения воздуха. Погрешность при
расчётах по этой формуле не превышает
0,1—0,5 % от измеряемой высоты. Более
точна формула Лапласа, учитывающая
влияние влажности воздуха и изменение
ускорения свободного падения.
Средние
скорости молекул, газа очень велики -
порядка сотен метров в секунду при
обычных условиях. Однако процесс
выравнивая неоднородности в газе
вследствие молекулярного движения
протекает весьма медленно. Это объясняется
тем, что молекулы при перемещении
испытывают соударения с другими
молекулами. При каждом соударении
скорость молекулы изменяется по величине
и направлению. Вследствие этого, скорость,
с которой молекула диффундирует из
одной части газа в другую, значительно
меньше средней скорости молекулярного
движения. Для оценки скорости движения
молекул вводится понятие средней длины
свободного пробега. Таким образом,
средняя дли свободного пробега
![]() -
это среднее расстояние, которое проходит
молекула от столкновения до столкновения.
-
это среднее расстояние, которое проходит
молекула от столкновения до столкновения.
Для
определения
вычислим
сначала среднее число соударений
![]() выбранной
молекулы с другими молекулами за единицу
времени. Будем считать, что молекула
после соударения продолжает двигаться
по прямой со средней скоростью движения
выбранной
молекулы с другими молекулами за единицу
времени. Будем считать, что молекула
после соударения продолжает двигаться
по прямой со средней скоростью движения
![]() .
.
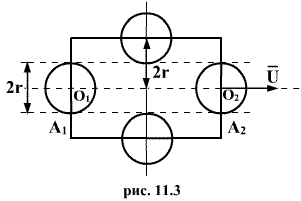
Молекулы,
с которыми соударяется выбранная
молекула, в первом приближении считаем
неподвижными и принимаем их за сферические
тела радиуса r. Пусть выбранная молекула
движется вправо из положения
![]() в
положение
в
положение
![]() по
прямой
по
прямой
![]() (рис.11.3).
При своем движении она испытывает
соударения с теми неподвижными молекулами,
центры которых лежат не дальше чем 2r от
траектории
.
Иными словами, движущаяся со средней
скоростью молекула в течении одной
секунды столкнется со всеми молекулами,
центры которых находятся в объеме
ограниченном цилиндром с радиусом 2r и
длиной
,
т.е.
(рис.11.3).
При своем движении она испытывает
соударения с теми неподвижными молекулами,
центры которых лежат не дальше чем 2r от
траектории
.
Иными словами, движущаяся со средней
скоростью молекула в течении одной
секунды столкнется со всеми молекулами,
центры которых находятся в объеме
ограниченном цилиндром с радиусом 2r и
длиной
,
т.е.
![]() .
.
Если концентрация молекул n , то внутри рассмотренного цилиндра находится число молекул, равное
![]()
Это число и определяет среднее число соударений за единицу времени.
Предположение
о том, что все молекулы, кроме одной,
неподвижны, является, конечно не верным.
В действительности все молекулы движутся,
и возможность соударения двух частиц
зависит от их относительной скорости.
Поэтому вместо среднеарифметической
скорости
должны
входить средняя относительная скорость
молекул
![]() .
Если скорости молекул распределены по
закону Максвелла, то, как можно показать,
средняя относительная скорость двух
молекул однородного газа в
.
Если скорости молекул распределены по
закону Максвелла, то, как можно показать,
средняя относительная скорость двух
молекул однородного газа в
![]() раз
превышает
.
Таким образом, среднее число соударений
должно быть увеличено в
раз
раз
превышает
.
Таким образом, среднее число соударений
должно быть увеличено в
раз
|
(11.7) |
Средний
путь, проходимый молекулой за единицу
времени, численно равен
.
Поэтому средняя длина свободного пробега
равна
![]() или
или
|
(11.8) |
Таким
образом, средняя длина свободного
пробега
не
зависит от температуры газа, т.к. с ростом
температуры одновременно возрастают
и
,
и
.
При подсчете числа соударений и средней
длины свободного пробега молекул за
модель молекулы было принято шарообразное
упругое тело. В действительности каждая
молекула представляет собой сложную
систему элементарных частиц и при
рассмотрении упругого соударения
молекул имелось в виду, что центры
молекул могут сблизиться до некоторого
наименьшего расстояния. Затем возникает
силы отталкивания которые вызывают
взаимодействие, подобное взаимодействию
при упругом ударе. Среднее расстояние
между центрами молекул, взаимодействующих,
как при упругом ударе, называют эффективным
диаметром
![]() .
Тогда
.
Тогда
|
(11.9) |
17. Итак, в термодинамических неравновесных системах возникают особые необратимые процессы, называемые явлениями переноса, в результате которых происходит пространственный перенос энергии, массы, импульса.
К явлениям переноса относятся теплопроводность, обусловленная переносам энергии, диффузия, обусловленная переносом массы, и внутреннее трение, обусловленное переносом импульса. Для простоты ограничимся одномерными явлениями переноса. Систему отсчета выберем так, чтобы ось x была ориентирована в направлении переноса.
1)Теплопроводность.
Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул друг с другом происходит процесс выравниваний средних кинетических энергий молекул, т.е., иными словами, выравнивание температур.
Перенос энергии в форме теплоты подчиняется закону Фурье:
![]()
Это величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси x. λ– теплопроводность, или коэффициент теплопроводности. dt / dx– градиент температуры, равный скорости изменения температуры на единицу длины x в направлении нормалей единичной площадки. Знак «–» показывает, что при теплопроводности энергия переносится в направлении убывания температуры.
Физический смысл коэффициента теплопроводности.
Коэффициент теплопроводности λ численно равен плотности теплового потока при градиенте температуры равной единице. Также коэффициент теплопроводности может быть рассчитан по формуле:
![]()
где CV– удельная теплоемкость газа при постоянном объеме, ρ– плотность газа, <v>– среднеарифметическая скорость теплового движения молекул, <l>– длина свободного пробега.
2)Диффузия.
Явление диффузии заключается в том, что происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел. Диффузия сводится к обмену масс частиц у этих тел, возникает и продолжается пока существует градиент плотности. Явление диффузии для химически однородного газа подчиняется закону Фика:
![]()
где jm– плотность потока массы – величина, определяемая массой вещества диффундирующего в единицу времени через единичную площадку, перпендикулярную оси x, D– коэффициент диффузии, dρ / dx– градиент плотности, определяемый скоростью изменения плотности на единицу длины x в направлении нормали, построенной в данной площадке. Знак «–» показывает, что перенос массы происходит в направлении убывания плотности. Коэффициент диффузии численно равен плотности потока массы при градиенте плотности равном единице. Согласно кинетической теории газа,
![]()
3)Внутреннее трение (вязкость).
Механизм возникновения внутреннего трения между параллельными слоями газа или жидкости, движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего, импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее, увеличивается, что приводит к торможению слоя, движущегося быстрее, и к ускорению слоя, движущегося медленнее. Сила внутреннего трения между двумя слоями газа или жидкости подчиняется закону Ньютона
![]()
где η– динамическая вязкость, dv / dx– градиент скорости, показывающий быстроту изменения скорости в направлении оси x перпендикулярно направлению движения слоев, S– площадь, на которую действует сила F.
Взаимодействие двух слоев, согласно второму закону Ньютона, можно рассматривать как процесс, при котором от одного слоя к другому в единицу времени передается импульс, по модулю равный действующей силе. Тогда выражение (5) можно представить в виде
![]()
где jp– плотность потока импульса – это величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси x через единичную площадку, перпендикулярную этой оси, dv / dx– градиент скорости. Знак «–» указывает, что импульс переносится в направлении убывания скорости.
Динамическая вязкость численно равна плотности потока импульса при градиенте скорости равном единице. Ее можно вычислить по формуле
![]()
Из сопоставления формул (1), (6), (3), описывающих явление переноса, следует, что закономерности всех явлений сходны между собой. Эти законы были установлены задолго до того, как они были обоснованы и выведены из МКТ, позволившей установить, что внешние сходства их математических выражений обусловлены общностью, лежащего в основе явлений теплопроводности, диффузии внутреннего трения молекулярного механизма – перемешивание молекул в процессе их хаотического движения и столкновения друг с другом.
Рассмотренные законы Фурье, Фика и Ньютона не вскрывают молекулярно кинетического смысла коэффициентов λ, D и η. Выражения для коэффициентов переноса записаны без вывода, т.к. строгое рассмотрение явлений переноса довольно громоздко, а качественное не имеет смысла.
Формулы (2), (4) и (7) связывают коэффициенты переноса и характеристики теплового движения молекул. Используя эти формулы, можно по найденным из опыта данным зная одни величины определить другие.
18.
Будем
искать выражение в общем виде для внешней
работы, которую совершает газ при
изменении его объема. Рассмотрим,
например, газ, который находится под
поршнем в цилиндрическом сосуде (рис.
1). Если газ, расширяясь, передвигает
поршень на бесконечно малое расстояние
dl,
то он осуществляет над
ним
работу
![]() где
S — площадь поршня, Sdl=dV—
изменение объема газа. Таким образом,
где
S — площадь поршня, Sdl=dV—
изменение объема газа. Таким образом,
![]() (1)
Полную работу А, которую совершает
газ при изменении его объема от V1
до V2,
найдем интегрированием формулы (1):
(1)
Полную работу А, которую совершает
газ при изменении его объема от V1
до V2,
найдем интегрированием формулы (1):
![]() (2)
Результат интегрирования зависит
от вида зависимости между давлением и
объемом газа. Найденное для работы
выражение (2) справедливо при любых
изменениях объема твердых, жидких и
газообразных тел.
Осуществленную
в том или ином процессе работу можно
изобразить графически с помощью кривой
в координатах р, V. Пусть, например,
изменение давления газа при его расширении
изображается кривой на рис. 2. При
увеличении объема на dV совершаемая
газом работа равна pdV, т. е. определяется
площадью полоски с основанием dV, которая
заштрихована на рисунке. Значит полная
работа, которая совершается газом при
расширении от объема V1
до объема V2,
определяется площадью, ограниченной
осью абсцисс, кривой p=f(V) и прямыми V1
и V2.
(2)
Результат интегрирования зависит
от вида зависимости между давлением и
объемом газа. Найденное для работы
выражение (2) справедливо при любых
изменениях объема твердых, жидких и
газообразных тел.
Осуществленную
в том или ином процессе работу можно
изобразить графически с помощью кривой
в координатах р, V. Пусть, например,
изменение давления газа при его расширении
изображается кривой на рис. 2. При
увеличении объема на dV совершаемая
газом работа равна pdV, т. е. определяется
площадью полоски с основанием dV, которая
заштрихована на рисунке. Значит полная
работа, которая совершается газом при
расширении от объема V1
до объема V2,
определяется площадью, ограниченной
осью абсцисс, кривой p=f(V) и прямыми V1
и V2.
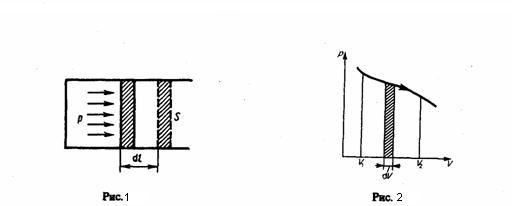
Графически можно представлять только равновесные процессы — процессы, которые состоят из последовательности равновесных состояний. Они протекают таким образом, что изменение термодинамических параметров за конечный промежуток времени бесконечно мало. Все реальные процессы не являются равновесными (они протекают с конечной скоростью), но в ряде случаев неравновесностью реальных процессов можно пренебречь (чем медленнее протекает процесс, тем он ближе к равновесному). В классической термодинамике рассматриваемые процессы предполагаются равновесными.
Коли́чество теплоты́ — энергия, которую получает или теряет тело при теплопередаче. Количество теплоты является одной из основных термодинамических величин.
Количество теплоты является функцией процесса, а не функцией состояния, то есть количество теплоты, полученное системой, зависит от способа, которым она была приведена в текущее состояние.
Единица измерения в Международной системе единиц (СИ): Джоуль.
Теплообмен — это процесс изменения внутренней энергии без совершения работы над телом или самим телом. Теплообмен всегда происходит в определенном направлении: от тел с более высокой температурой к телам с более низкой. Когда температуры тел выравниваются, теплообмен прекращается. Теплообмен может осуществляться тремя способами:
теплопроводностью
конвекцией
излучением
Теплопроводность
Теплопроводность — явление передачи внутренней энергии от одной части тела к другой или от одного тела к другому при их непосредственном контакте. Наибольшей теплопроводностью обладают металлы — она у них в сотни раз больше, чем у воды. Исключением являются ртуть и свинец, но и здесь теплопроводность в десятки раз больше, чем у воды. При опускании металлической спицы в стакан с горячей водой очень скоро конец спицы становился тоже горячим. Следовательно, внутренняя энергия, как и любой вид энергии, может быть передана от одних тел к другим. Внутренняя энергия может передаваться и от одной части тела к другой. Так, например, если один конец гвоздя нагреть в пламени, то другой его конец, находящийся в руке, постепенно нагреется и будет жечь руку. Нагревание кастрюли на электрической плитке происходит через теплопроводность. Изучим это явление, проделав ряд опытов с твердыми телами, жидкостью и газом. Внесем в огонь конец деревянной палки. Он воспламенится. Другой конец палки, находящийся снаружи, будет холодным. Значит, дерево обладает плохой теплопроводностью. Поднесем к пламени спиртовки конец тонкой стеклянной палочки. Через некоторое время он нагреется, другой же конец, останется холодным. Следовательно, и стекло имеет плохую теплопроводность. Если же мы будем нагревать в пламени конец металлического стержня, то очень скоро весь стержень сильно нагреется. Удержать его в руках мы уже не сможем. Значит, металлы хорошо проводят тепло, т. е. имеют большую теплопроводность. Наибольшей теплопроводностью обладают серебро и медь. Теплопроводность у различных веществ различна. Плохой теплопроводностью обладают шерсть, волосы, перья птиц, бумага, пробка и другие пористые тела. Это связано с тем, что между волокнами этих веществ содержится воздух. Самой низкой теплопроводностью обладает вакуум (освобожденное от воздуха пространство). Объясняется это тем, что теплопроводность — это перенос энергии от одной части тела к другой, который происходит при взаимодействии молекул или других частиц. В пространстве, где нет частиц, теплопроводность осуществляться не может. Если возникает необходимость предохранить тело от охлаждения или нагревания, то применяют вещества с малой теплопроводностью. Так, для кастрюль, сковородок ручки из пластмассы. Дома строят из бревен или кирпича, обладающих плохой теплопроводностью, а значит, предохраняют от охлаждения.
Конвекция
Конвекция — это процесс теплопередачи, осуществляемый путем переноса энергии потоками жидкости или газа. Пример явления конвекции: небольшая бумажная вертушка, поставленная над пламенем свечи или электрической лампочкой, под действием поднимающегося нагретого воздуха начинает вращаться. Это явление можно объяснить таким образом. Воздух, соприкасаясь с теплой лампой, нагревается, расширяется и становится менее плотным, чем окружающий его холодный воздух. Сила Архимеда, действующая на теплый воздух со стороны холодного снизу вверх, больше, чем сила тяжести, которая действует на теплый воздух. В результате нагретый воздух «всплывает», поднимается вверх, а его место занимает холодный воздух. При конвекции энергия переносится самими струями газа или жидкости. Различают два вида конвекции:
естественная (или свободная)
Возникает в веществе самопроизвольно при его неравномерном нагревании. При такой конвекции нижние слои вещества нагреваются, становятся легче и всплывают, а верхние слои, наоборот, остывают, становятся тяжелее и опускаются вниз, после чего процесс повторяется.
вынужденная
Наблюдается при перемешивании жидкости мешалкой, ложкой, насосом и т. д. Для того, чтобы в жидкостях и газах происходила конвекция, необходимо их нагревать снизу. Конвекция в твердых телах происходить не может.
Излучение
Излучение — электромагнитное излучение, испускаемое за счет внутренней энергии веществом, находящимся при определенной температуре. Мощность теплового излучения объекта, удовлетворяющего критериям абсолютно черного тела, описывается законом Стефана — Больцмана. Отношение излучательной и поглощательной способностей тел описывается законом излучения Кирхгофа. Передача энергии излучением отличается от других видов теплопередачи: она может осуществляться в полном вакууме. Излучают энергию все тела: и сильно нагретые, и слабо, например тело человека, печь, электрическая лампочка и др. Но чем выше температура тела, тем больше энергии передает оно путем излучения. При этом энергия частично поглощается этими телами, а частично отражается. При поглощении энергии тела нагреваются по-разному, в зависимости от состояния поверхности. Тела с темной поверхностью лучше поглощают и излучают энергию, чем тела, имеющие светлую поверхность. В то же время тела с темной поверхностью охлаждаются быстрее путем излучения, чем тела со светлой поверхностью. Например, в светлом чайнике горячая вода дольше сохраняет высокую температуру, чем в темном.
Согласно
закону Джоуля, выведенному эмпирически,
внутренняя энергия идеального
газа не зависит от давления или
объёма. Исходя из этого факта, можно
получить выражение для изменения
внутренней энергии идеального газа. По
определению молярной
теплоёмкости при постоянном
объёме,
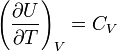 .
Так как внутренняя энергия идеального
газа является функцией только от
температуры, то
.
Так как внутренняя энергия идеального
газа является функцией только от
температуры, то
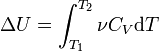 .
.
Эта
же формула верна и для вычисления
изменения внутренней энергии любого
тела, но только в процессах при постоянном
объёме (изохорных
процессах); в общем случае
![]() является
функцией и температуры, и объёма.
является
функцией и температуры, и объёма.
Если пренебречь изменением молярной теплоёмкости при изменении температуры, получим:
![]() ,
,
где
![]() —
количество вещества,
—
количество вещества,
![]() —
изменение температуры.
—
изменение температуры.
Первый закон термодинамики является обобщением закона сохранения и превращения энергии для термодинамической системы. Он формулируется следующим образом:
Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами.
|
Соотношение, выражающее первый закон термодинамики, часто записывают в другой форме:
|
Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами.
Применим первый закон термодинамики к изопроцессам в газах.
В изохорном процессе (V = const) газ работы не совершает, A = 0. Следовательно,
|
Здесь U (T1) и U (T2) – внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит только от температуры (закон Джоуля). При изохорном нагревании тепло поглощается газом (Q > 0), и его внутренняя энергия увеличивается. При охлаждении тепло отдается внешним телам (Q < 0).
В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением
|
Первый закон термодинамики для изобарного процесса дает:
|
При изобарном расширении Q > 0 – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии Q < 0 – тепло отдается внешним телам. В этом случае A < 0. Температура газа при изобарном сжатии уменьшается, T2 < T1; внутренняя энергия убывает, ΔU < 0.
В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, ΔU = 0.
Первый закон термодинамики для изотермического процесса выражается соотношением
|
Количество теплоты Q, полученной газом в процессе изотермического расширения, превращается в работу над внешними телами. При изотермическом сжатии работа внешних сил, произведенная над газом, превращается в тепло, которое передается окружающим телам.
Наряду с изохорным, изобарным и изотермическим процессами в термодинамике часто рассматриваются процессы, протекающие в отсутствие теплообмена с окружающими телами. Сосуды с теплонепроницаемыми стенками называются адиабатическими оболочками, а процессы расширения или сжатия газа в таких сосудах называются адиабатическими. 4. В адиабатическом процессе Q = 0; поэтому первый закон термодинамики принимает вид
|
т. е. газ совершает работу за счет убыли его внутренней энергии.
19. Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус:
|
|
|
(4.2.1) |
Размерность теплоемкости: [C] = Дж/К.
Однако, теплоёмкость – величина неопределённая, поэтому пользуются понятиями удельной и молярной теплоёмкости.
Удельная теплоёмкость (Суд) есть количество теплоты, необходимое для нагревания единицы массы вещества на 1 градус [Cуд] = Дж/К.
Для газов удобно пользоваться молярной теплоемкостью Cμ- количество теплоты, необходимое для нагревания 1 моля газа на 1 градус:
|
|
|
(4.2.2) |
[Cμ] = Дж/(моль×К).
Из п. 1.2 известно, что молярная масса – масса одного моля:
|
|
|
|
где А – атомная масса; mед - атомная единица массы; NА - число Авогадро; моль μ – количество вещества, в котором содержится число молекул, равное числу атомов в 12 г изотопа углерода 12С.
Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании.
Если газ нагревать при постоянном объёме, то всё подводимое тепло идёт на нагревание газа, то есть изменение его внутренней энергии. Теплоёмкость при этом обозначается СV.
СР – теплоемкость при постоянном давлении. Если нагревать газ при постоянном давлении Р в сосуде с поршнем, то поршень поднимется на некоторую высоту h, то есть газ совершит работу (рис. 4.2).
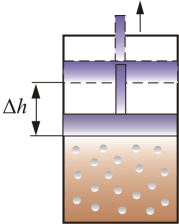 Рис.
4.2
Рис.
4.2
Следовательно,
проводимое тепло затрачивается и на
нагревание и на совершение работы.
Отсюда ясно, что
![]() .
.
Итак, проводимое тепло и теплоёмкость зависят от того, каким путём осуществляется передача тепла. Значит, Q и С не являются функциями состояния.
Величины СР и СV оказываются связанными простыми соотношениями. Найдём их.
Пусть мы нагреваем один моль идеального газа при постоянном объёме(dA = 0). Тогда первое начало термодинамики запишем в виде:
|
|
|
(4.2.3) |
т.е.
бесконечно малое приращение количества
теплоты
![]() равно
приращению внутренней энергии dU.
равно
приращению внутренней энергии dU.
Теплоемкость при постоянном объёме будет равна:
|
|
|
(4.2.4) |
В общем случае
|
|
|
|
так как U может зависеть не только от температуры. Но в случае идеального газа справедлива формула (4.2.4).
Из
(4.2.4) следует, что
![]()
|
|
|
|
|
|
|
(4.2.5) |
Внутренняя энергия идеального газа является только функцией температуры (и не зависит от V, Р и тому подобных), поэтому формула (4.2.5) справедлива для любого процесса.
Для произвольной идеальной массы газа:
|
|
|
(4.2.6) |
При изобарическом процессе, кроме увеличения внутренней энергии, происходит совершение работы газом:
|
|
|
|
|
|
|
(4.2.7) |
Из
основного уравнения молекулярно-кинетической
теории
![]() .
При изобарическом процессе Р = const.
Следовательно, из (4.2.7) получим:
.
При изобарическом процессе Р = const.
Следовательно, из (4.2.7) получим:
|
|
|
(4.2.8) |
Это уравнение Майера для одного моля газа.
Из этого следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус в изобарическом процессе.
Используя это соотношение, Роберт Майер в 1842 г. вычислил механический эквивалент теплоты: 1 кал = 4,19 Дж.
Полезно знать формулу Майера для удельных теплоёмкостей:
|
|
|
|
или
|
|
Адиабати́ческий, или адиаба́тный проце́сс — термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством.
Адиабата Пуассона
Для идеальных газов, чью теплоёмкость можно считать постоянной, в случае квазистатического процесса адиабата имеет простейший вид и определяется уравнением[6][15][16]
![]()
где
![]() —
его объём,
—
его объём,
![]() —
показатель
адиабаты,
—
показатель
адиабаты,
![]() и
и
![]() —
теплоёмкости
газа соответственно при постоянном
давлении и постоянном объёме.
—
теплоёмкости
газа соответственно при постоянном
давлении и постоянном объёме.
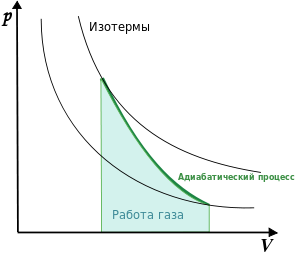
![]()
График адиабаты
(жирная линия) на
![]() диаграмме
для газа.
—
давление газа;
диаграмме
для газа.
—
давление газа;
![]() —
объём.
—
объём.
С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду
![]()
где — абсолютная температура газа. Или к виду
![]()
Поскольку
![]() всегда
больше 1, из последнего уравнения следует,
что при адиабатическом сжатии (то есть
при уменьшении
)
газ нагревается (
возрастает), а при расширении —
охлаждается, что всегда верно и для
реальных газов. Нагревание при сжатии
больше для того газа, у которого больше
коэффициент
.
всегда
больше 1, из последнего уравнения следует,
что при адиабатическом сжатии (то есть
при уменьшении
)
газ нагревается (
возрастает), а при расширении —
охлаждается, что всегда верно и для
реальных газов. Нагревание при сжатии
больше для того газа, у которого больше
коэффициент
.

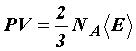 и
и
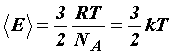 .
(31)
.
(31)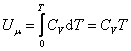 ,
,