Сохранение механической энергии

Закон сохранения механической энергии утверждает, что если тело или система подвергается действию только консервативных сил, то полная механическая энергия этого тела или системы остаётся постоянной. В изолированной системе, где действуют только консервативные силы, полная механическая энергия сохраняется

Абсолю́тно неупру́гий удар — удар, в результате которого компоненты скоростей тел, нормальные площадке касания, становятся равными. Если удар был центральным (скорости были перпендикулярны касательной плоскости), то тела соединяются и продолжают дальнейшее своё движение как единое тело.

Где v это общая скорость тел, полученная после удара, m_a - масса первого тела, u_a - скорость первого тела до соударения. m_b - масса второго тела, u_b -скорость второго тела до соударения. Важно - импульсы являются величинами векторными, поэтому складываются только векторно.

Как и при любом ударе, при этом выполняются закон сохранения импульса и закон сохранения момента импульса, но не выполняется закон сохранения механической энергии. Часть кинетической энергии соудареямых тел в результате неупругих деформаций переходит в тепловую.

Хорошая модель абсолютно неупругого удара — сталкивающиеся пластилиновые шарики.

Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков. Математическая модель абсолютно упругого удара работает примерно следующим образом:

1. Есть в наличии два абсолютно твердых тела, которые сталкиваются

2. В точке контакта происходят упругие деформации. Кинетическая энергия движущихся тел мгновенно переходит в энергию деформации.

3. В следующий момент деформированные тела принимают свою прежнюю форму, а энергия деформации вновь переходит в кинетическую энергию.

4. Контакт тел прекращается и они продолжают движение.

Для математического описания простейших абсолютно упругих ударов, используется закон сохранения энергии и закон сохранения импульса.

Здесь m₁, m₂ - массы первого и второго тел. u₁, v₁ - скорость первого тела до, и после взаимодействия. u₂, v₂ - скорость второго тела до, и после взаимодействия.

Важно - импульсы складываются векторно, а энергии скалярно.

11. Уравнение неразрывности

 Рассмотрим участок элементарной струи жидкости, который ограничен двумя нормальными сечениями с площадями и (рис.1). Скорости течения жидкости в сечениях и равны соответственно и .  В стационарном потоке масса жидкости, протекающая за время через сечение равна массе жидкости, протекающей за то же время через сечение : . Учитывая, что , ,  получаем:

            (1).

Уравнение (1) называется уравнением неразрывности.

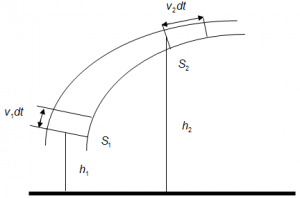
Рис.1. Трубка тока

Уравнение Бернулли

Для перемещения жидкости находящегося в объеме в объем силы давления выполняют работу

   (2)

Работа сил давления равна приращению полной энергии выделенного объема жидкости:

   (3)

Приравнивая правые части уравнений (2) и (3), после элементарных преобразований получаем:

(4)

Это уравнение называется уравнением Бернулли.

В случае, если оба сечения трубки тока находятся на одной высоте, уравнение приобретает более простой вид:

(5)

Жидкость, в которой при любых движениях  не возникают силы внутреннего трения, называют идеальной.

12.