
- •3. Основная задача динамики
- •9. Кинетическая и потенциальная энергия
- •Сохранение механической энергии
- •11. Уравнение неразрывности
- •Уравнение Бернулли
- •Закон Стокса
- •Вывод уравнения
- •Показатель адиабаты
- •Кпд тепловой машины Карно
- •Связь между обратимостью цикла и кпд
- •Уравнение состояния
- •Условие равновесия фаз
- •Уравнение Клапейрона — Клаузиуса
- •Классификация фазовых переходов
- •Динамика фазовых переходов
- •Формула Лапласа
1 и
2. Кинематическое
описание движения материальной
точки
материальная
точка –
тело, обладающее массой, размерами
которого в данной задаче можно
пренебречь.
Система
отсчета
это совокупность системы координат и
часов, связанных с телом отсчета.
 Вектор
Вектор![]() ,
т. е. приращение радиус-вектора точки
за рассматриваемый промежуток времени,
называется
перемещением.
Траектория
движения материальной точки – линия,
описываемая этой точкой в пространстве.
Длина
участка траектории АВ,
пройденного материальной точкой с
момента начала отсчета времени, называется
длиной пути
,
т. е. приращение радиус-вектора точки
за рассматриваемый промежуток времени,
называется
перемещением.
Траектория
движения материальной точки – линия,
описываемая этой точкой в пространстве.
Длина
участка траектории АВ,
пройденного материальной точкой с
момента начала отсчета времени, называется
длиной пути
![]() Вектором
средней скорости
<v>
называется отношение приращения
Вектором
средней скорости
<v>
называется отношение приращения
![]() радиус-вектора
точки к промежутку времени
радиус-вектора
точки к промежутку времени
![]() :
:
![]()
|
|
Направление
вектора средней скорости совпадает с
направлением
![]() .
При неограниченном уменьшении
.
При неограниченном уменьшении
![]() средняя
скорость стремится к предельному
значению, которое называется
мгновенной скоростью
v:
средняя
скорость стремится к предельному
значению, которое называется
мгновенной скоростью
v:
![]()
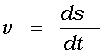
 Средним
ускорением
неравномерного движения в интервале
от t
до
Средним
ускорением
неравномерного движения в интервале
от t
до
![]() называется
векторная величина, равная отношению
изменения скорости
называется
векторная величина, равная отношению
изменения скорости
![]() к
интервалу времени
:
к
интервалу времени
:
![]() Мгновенным
ускорением a
(ускорением) материальной точки в момент
времени t
будет предел среднего
ускорения:
Мгновенным
ускорением a
(ускорением) материальной точки в момент
времени t
будет предел среднего
ускорения:
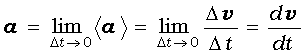 Криволинейное
движение
Тангенциальная
составляющая ускорения
Криволинейное
движение
Тангенциальная
составляющая ускорения
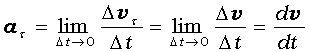 т.
е., определяет быстроту изменения
скорости по модулю.
Вторая
составляющая ускорения, равная
т.
е., определяет быстроту изменения
скорости по модулю.
Вторая
составляющая ускорения, равная
![]() называется
нормальной составляющей ускорения
и направлена по нормали к траектории к
центру се кривизны (поэтому ее называют
также
центростремительным
ускорением).
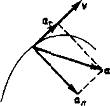
Полное
ускорение
тела есть геометрическая сумма
тангенциальной и нормальной составляющих
(рис. 1.5):
называется
нормальной составляющей ускорения
и направлена по нормали к траектории к
центру се кривизны (поэтому ее называют
также
центростремительным
ускорением).
Полное
ускорение
тела есть геометрическая сумма
тангенциальной и нормальной составляющих
(рис. 1.5):
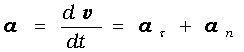
|
тангенциальная
составляющая ускорения характеризует
быстроту
изменения скорости по модулю
(направлена по касательной к траектории),
а нормальная
составляющая ускорения – быстроту
изменения скорости по направлению
(направлена к центру кривизны
траектории).
Равнопеременное
движение
![]() В
зависимости от тангенциальной и
нормальной составляющих ускорения
движение можно классифицировать
следующим образом:
1)
В
зависимости от тангенциальной и
нормальной составляющих ускорения
движение можно классифицировать
следующим образом:
1)
![]() ,
,![]() – прямолинейное равномерное движение;
2)
– прямолинейное равномерное движение;
2)
![]() ,
–
прямолинейное равнопеременное движение.
3)
,
–
прямолинейное равнопеременное движение.
3)![]() ,
–
прямолинейное движение с переменным
ускорением;
4)
,
,
–
прямолинейное движение с переменным
ускорением;
4)
,
![]() .
При
скорость
по модулю не изменяется, а изменяется
по направлению.
5)
,
.
При
скорость
по модулю не изменяется, а изменяется
по направлению.
5)
,
![]() –
равномерное криволинейное движение;
6)
–
равномерное криволинейное движение;
6)
![]() ,
–
криволинейное равнопеременное
движение;
7)
,
–
криволинейное движение с переменным
ускорением.
Вопрос3
Кинематика вращательного движения
,
–
криволинейное равнопеременное
движение;
7)
,
–
криволинейное движение с переменным
ускорением.
Вопрос3
Кинематика вращательного движения
 Угловой
скоростью называется векторная величина,
равная первой производной угла поворота
тела по времени:
Угловой
скоростью называется векторная величина,
равная первой производной угла поворота
тела по времени:
![]() Вектор
Вектор
![]() так
же, как и вектор
так
же, как и вектор
![]() .
Размерность угловой скорости
.
Размерность угловой скорости
![]() ,
а ее единица – радиан в секунду
(рад/с).
,
а ее единица – радиан в секунду
(рад/с).
![]() Угловым
ускорением
называется векторная величина, равная
первой производной угловой скорости
по времени:
Тангенциальная
составляющая ускорения
Угловым
ускорением
называется векторная величина, равная
первой производной угловой скорости
по времени:
Тангенциальная
составляющая ускорения
![]()
![]() и
и
![]() .
Нормальная
составляющая ускорения
.
Нормальная
составляющая ускорения
![]() .
Таким
образом, связь между линейными (длина
пути s,
пройденного точкой по дуге окружности
радиуса R,
линейная скорость v,
тангенциальное ускорение
.
Таким
образом, связь между линейными (длина
пути s,
пройденного точкой по дуге окружности
радиуса R,
линейная скорость v,
тангенциальное ускорение
![]() нормальное
ускорение
нормальное
ускорение
![]() )
и угловыми величинами (угол поворота
)
и угловыми величинами (угол поворота
![]() ,
угловая скорость
,
угловая скорость
![]() ,
угловое ускорение
,
угловое ускорение
![]() )
выражается следующими формулами:
)
выражается следующими формулами:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
3. Основная задача динамики
Исторически деление на прямую и обратную задачу динамики сложилось следующим образом.
Прямая задача динамики: по заданному характеру движения определить равнодействующую сил, действующих на тело.
Обратная задача динамики: по заданным силам определить характер движения тела.
Масса тела - физическая величина, определяющая ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства. В настоящее время можно считать доказанным, что гравитационная и инертная массы численно совпадают. для описания воздействия, упоминаемые в первом законе Ньютона, вводят понятие силы. Под действием сил тело либо изменяют скорость движения, т. е. приобретают ускорения (динамическое проявление сил), либо деформируются, т. е. изменяют свою форму и размеры (статическое проявление сил). В каждый момент времени сила характеризуется числовым значением, направлением в пространстве и точкой приложения. Итак, сила - это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры. И́мпульс (Количество движения) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:
![]() .
.
Классическая динамика основана на трёх основных законах Ньютона:
1-й: Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано.
![]()
2-й: В инерциальной системе отсчета сумма всех сил, действующих на тело, равна произведению массы этого тела на векторное ускорение этого же тела (действие на тело силы, проявляется в сообщении ему ускорения).
![]()
![]()
В наиболее общем случае, который описывает также движение тела с изменяющейся массой (например, реактивное движение), 2-й закон Ньютона принято записывать следующим образом:
![]() ,
,
где
![]() —
импульс
тела. Таким образом, сила характеризует
быстроту изменения импульса.
—
импульс
тела. Таким образом, сила характеризует
быстроту изменения импульса.
3-й: Тела действуют друг на друга силами равными по модулю и противоположными по направлению
![]()
![]()
Если при этом рассматриваются взаимодействующие материальные точки, то обе эти силы действуют вдоль прямой, их соединяющей. Это приводит к тому, что суммарный момент импульса системы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохранения импульса и момента импульса
4. Импульс системы материальных точек - это векторная сумма импульсов всех материальных точек, входящих в систему

Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная. Фундаментальность законов сохранения заключается в их универсальности. Они справедливы при изучении любых физических процессов (механических, тепловых, электромагнитных и др.). Они одинаково применимы в релятивистском и нерелятивистском движении, в микромире, где справедливы квантовые представления, и в макромире, с его классическими представлениями.
5. Абсолю́тно твёрдое те́ло — второй опорный объект механики наряду с материальной точкой. Механика абсолютно твердого тела полностью сводима к механике материальных точек (с наложенными связями), но имеет собственное содержание (полезные понятия и соотношения, которые могут быть сформулированы в рамках модели абсолютно твердого тела), представляющее большой теоретический и практический интерес.
Существует несколько определений:
Абсолютно твёрдое тело — модельное понятие классической механики, обозначающее совокупность материальных точек, расстояния между которыми сохраняются в процессе любых движений, совершаемых этим телом. Иначе говоря, абсолютно твердое тело не только не изменяет свою форму, но и сохраняет неизменным распределение массы внутри.
Абсолютно твёрдое тело — механическая система, обладающая только поступательными и вращательными степенями свободы. «Твёрдость» означает, что тело не может быть деформировано, то есть телу нельзя передать никакой другой энергии, кроме кинетической энергии поступательного или вращательного движения.
Абсолютно твёрдое тело — тело (система), взаимное положение любых точек которого не изменяется, в каких бы процессах оно ни участвовало.
Таким образом, положение абсолютно твердого тела полностью определяется, например, положением жестко привязанной к нему декартовой системы координат (обычно ее начало координат делают совпадающим с центром масс твердого тела).
В трёхмерном пространстве и в случае отсутствия (других) связей абсолютно твёрдое тело обладает 6 степенями свободы: три поступательных и три вращательных. Исключение составляет двухатомная молекула или, на языке классической механики, твёрдый стержень нулевой толщины. Такая система имеет только две вращательных степени свободы.
Абсолютно твёрдых тел в природе не существует, однако в очень многих случаях, когда деформация тела мала и ей можно пренебречь, реальное тело может (приближенно) рассматриваться как абсолютно твёрдое тело без ущерба для задачи. Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
![]() ,
,
где:
mi — масса i-й точки,
ri — расстояние от i-й точки до оси.
Пусть тело вращается вокруг неподвижной нецентральной оси. Это тело обладает кинетической энергией
 , (1)
, (1)где I - момент инерции тела относительно данной нецентральной оси
 .
Проведём через центр масс С о
.
Проведём через центр масс С о сь ОО
, параллельную данной нецентральной
оси
. Тогда
вращение твёрдого тела можно представить
как результат вращения центра масс С
вокруг оси
и вращение твёрдого тела вокруг
центральной оси ОО тоже с угловой
скоростью .
Кинетическую энергию тоже можно
представить как сумму двух слагаемых
:
сь ОО
, параллельную данной нецентральной
оси
. Тогда
вращение твёрдого тела можно представить
как результат вращения центра масс С
вокруг оси
и вращение твёрдого тела вокруг
центральной оси ОО тоже с угловой
скоростью .
Кинетическую энергию тоже можно
представить как сумму двух слагаемых
: , (2)
, (2)где
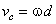 -
линейная скорость центра масс. C учётом
(1) и (2) получаем
-
линейная скорость центра масс. C учётом
(1) и (2) получаем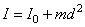 -
теорема Штейнера.
-
теорема Штейнера.Теорема Штейнера: Момент инерции I относительно произвольной оси равен сумме момента инерции I0 относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями :
Таким образом, теорема Штейнера, по существу, сводит вычисление момента инерции относительно произвольной оси к вычислению момента инерции относительно оси, проходящей через центр масс тела.
6.
Момент
силы—
векторная
физическая
величина,
равная векторному произведению
радиус-вектора,
(проведенного от оси
вращения
к точке приложения силы —
по определению), на вектор этой силы.
Характеризует вращательное действие
силы на твёрдое тело.
Моме́нт
и́мпульса
характеризует количество вращательного
движения.
Величина, зависящая от того, сколько
массы
вращается, как она распределена
относительно оси вращения и с какой
скоростью
происходит вращение.
Момент импульса
![]() частицы
относительно некоторого начала отсчёта
определяется векторным
произведением
её радиус-вектора
и импульса:
частицы
относительно некоторого начала отсчёта
определяется векторным
произведением
её радиус-вектора
и импульса:
![]()
где
![]() —
радиус-вектор частицы относительно
выбранного неподвижного в данной системе
отсчёта начала отсчёта,
—
радиус-вектор частицы относительно
выбранного неподвижного в данной системе
отсчёта начала отсчёта,
![]() —
импульс частицы.
—
импульс частицы.
Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:
![]()
где
![]() —
радиус-вектор и импульс каждой частицы,
входящей в систему, момент импульса
которой определяется.
—
радиус-вектор и импульс каждой частицы,
входящей в систему, момент импульса
которой определяется.
![]() -
уравнение динамики вращательного
движения твердого тела относительно
неподвижной оси z,
где Mz
– момент силы, Lz
– момент импульса, Jz
– момент инерции тела относительно оси
z,
-
уравнение динамики вращательного
движения твердого тела относительно
неподвижной оси z,
где Mz
– момент силы, Lz
– момент импульса, Jz
– момент инерции тела относительно оси
z,
![]() -
угловое ускорение.
-
угловое ускорение.
7.

Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить:
![]()
Если
тело вращается вокруг неподвижной оси
с угловой скоростью
![]() ,
то
линейная скорость i-ой точки равна
,
то
линейная скорость i-ой точки равна
![]() ,
где
,
где
![]() ,
- расстояние от этой точки до оси вращения.
Следовательно.
,
- расстояние от этой точки до оси вращения.
Следовательно.
|
(5.11) |
где
![]() -
момент инерции тела относительно оси
вращения.
-
момент инерции тела относительно оси
вращения.
В
общем случае движение твердого тела
можно представить в виде суммы двух
движений - поступательного со скоростью,
равной скорости
![]() центра
инерции тела, и вращения с угловой
скоростью
вокруг
мгновенной оси, проходящей через центр
инерции. При этом выражение для
кинетической энергии тела преобразуется
к виду
центра
инерции тела, и вращения с угловой
скоростью
вокруг
мгновенной оси, проходящей через центр
инерции. При этом выражение для
кинетической энергии тела преобразуется
к виду
|
(5.12) |
где
![]() -
момент инерции тела относительно
мгновенной оси вращения, проходящей
через центр инерции.
-
момент инерции тела относительно
мгновенной оси вращения, проходящей
через центр инерции.
8. Энергия — универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холодное), в других — переходит в иную форму (например, в результате трения механическое движение превращается в тепловое). Однако существенно, что во всех случаях энергия, отданная (в той или иной форме) одним телом другому телу, равна энергии, полученной последним телом.
Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы.
Если
тело движется прямолинейно и на него
действует постоянная сила
![]() ,
которая составляет некоторый угол а с
направлением перемещения, то работа
этой силы равна произведению проекции
силы
,
которая составляет некоторый угол а с
направлением перемещения, то работа
этой силы равна произведению проекции
силы
![]() ,
на направление перемещения (
,
на направление перемещения (![]() ),
умноженной на перемещение точки
приложения силы:
),
умноженной на перемещение точки
приложения силы:
![]() .
.
В
общем случае сила может изменяться как
по модулю, так и по направлению, поэтому
этой формулой пользоваться нельзя.
Если, однако, рассмотреть элементарное
перемещение
![]() ,
то силу
,
то силу
![]() можно
считать постоянной, а движение точки
ее приложения — прямолинейным.
Элементарной работой силы
на
перемещении
называется
скалярная величина
можно
считать постоянной, а движение точки
ее приложения — прямолинейным.
Элементарной работой силы
на
перемещении
называется
скалярная величина
![]()
где
![]() —
угол между векторами
и
;
—
угол между векторами
и
;
![]() —
элементарный путь;
—
проекция вектора
на
вектор
.
—
элементарный путь;
—
проекция вектора
на
вектор
.
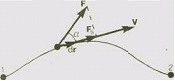
Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Эта сумма приводится к интегралу
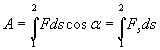 .
.
Для
вычисления этого интеграла надо знать
зависимость силы
,
от пути
![]() вдоль
траектории 1—2. Пусть эта зависимость
представлена графически
вдоль
траектории 1—2. Пусть эта зависимость
представлена графически
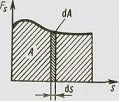
тогда
искомая работа А определяется на графике
площадью заштрихованной фигуры. Если,
например, тело движется прямолинейно,
сила
![]() и
и
![]() ,
то получим
,
то получим
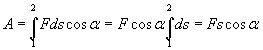 ,
,
где — пройденный телом путь.
При
![]() работа
силы положительна, в этом случае
составляющая
,
совпадает по направлению с вектором
скорости движения
работа
силы положительна, в этом случае
составляющая
,
совпадает по направлению с вектором
скорости движения
![]() .
Если
.
Если![]() ,
то работа силы отрицательна. При
,
то работа силы отрицательна. При
![]() (сила
направлена перпендикулярно перемещению)
работа силы равна нулю.
(сила
направлена перпендикулярно перемещению)
работа силы равна нулю.
Единица работы — джоуль (Дж): 1 Дж — работа, совершаемая силой 1 Н на пути 1 м (1 Дж=1 Н-м).
Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:
![]() .
.
За
время
![]() сила
совершает
работу
сила
совершает
работу
![]() ,
и мощность, развиваемая этой силой, в
данный момент времени
,
и мощность, развиваемая этой силой, в
данный момент времени
![]() ,
,
т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N — величина скалярная.
Единица мощности — ватт (Вт): 1 Вт — мощность, при которой за время 1 с. совершается работа 1 Дж (1 Вт=1 Дж/с).
В физике консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил)[1]. Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0. Примерами консервативных сил являются: сила тяжести, сила упругости, сила кулоновского (электростатического) взаимодействия. Примерами неконсервативных сил являются сила трения и сила сопротивления среды.
