35. Проверка гипотезы о равенстве средних значении для нормального распределения при известной и неизвестной генеральной дисперсиях.

Пусть Х1 є N(a1, σ1), X2 є N(a2, σ2) и дисперси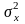и и 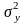известны (вместо х и у – 1 и 2). Имеются выборки {x1, x2,…,xn1} и{y1, y2,…, yn2} из генеральных совокупностей Х1 иХ2.

Гипотеза состоит в том, что средние распределений равны, т.е. : а1=а2, при этом Н1: а1≠а2.

Если выполняется гипотеза , то статистика будет иметь стандартное нормальное распределение N(0;1) и на заданном уровне доверия γ гипотеза проверяется, где t вычисляется по формуле: .

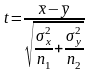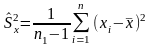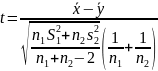Если же дисперсии и неизвестны, но равны, то доказано, что в случае справедливости гипотезы статистика имеет распределение Стьюдента с k=n1+n2 – 2 степенями свободы. Здесь S1 и S2 в квадрате «неисправленные» выборочные дисперсии, т.е.: или . (1)

Для заданного уровня доверия γ по таблицам распределения Стьюдента находим tк,кр из условия P{|tк|<tк,кр}=γ, и гипотеза принимается, если полученное после вычислений по формуле (1) значение tк удовлетворяет неравенству |tк|<tк,кр.

Если n>30, то распределения средних х и у можно считать приближенно нормальными.

36. Критерий Пирсона.

В наиболее часто используемом на практике критерии - Пирсона в качестве меры расхождения 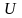берется величина , равная относительной сумме квадратов отклонений межу эмпирическими 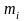и теоретическими 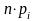частотами попадания в интервалы 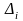: , где -число интервалов эмпирического распределения (вариационного ряда), - объем выборки, 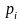- вероятность попадания случайной величины в интервал , вычисленная по закону распределения, соответствующему гипотезе .

Доказано, что при справедливости гипотезы и при 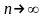критерий имеет - распределение со 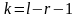степенями свободы, где 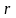- число параметров теоретического распределения, вычисленных по экспериментальным данным.

Следует отметить, что критерий имеет закон распределения лишь при . Поэтому этот критерий нельзя применять при малых объемах выборок. Поэтому необходимо чтобы в каждом интервале было не менее 5-10 выборочных значений, а весь объем выборки был порядка сотен.

37. Критерий согласия Фишера – Снедекора и его применение для проверки гипотезы о равенстве дисперсий.

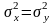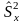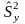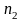Проверка гипотезы , о том, что дисперсии двух нормально распределенных генеральных совокупностей , сводится к сравнению выборочных «исправленных» дисперсий и , вычисляемые по двум независимым выборкам объемом и . В качестве критерия принимается отношение выборочных «исправленных» дисперсий и .

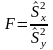Доказано, что при справедливости гипотезы критерий 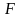представляет собой случайную величину с распределением Фишера-Снедекора с степенями свободы и .

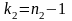Поэтому, выбрав необходимый уровень значимости по таблицам распределения Фишера-Снедекора, находим критическое значение .

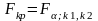Если 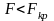, то гипотеза принимается.

38. Критерий согласия Колмогорова.

Критерий Колмогорова применяется в тех случаях, когда заранее известен не только вид распределения, но и числовые характеристики распределения. В этом критерии в качестве меры расхождения между теоретическими и эмпирическими распределениями рассматривают максимальное значение абсолютной величины разности между эмпирической функцией распре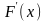деления и соответствующей теоретической функции распределения 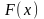: ,называемое статистикой критерия Колмогорова.

Доказано, что какова бы ни была функция распределения , при неограниченном увеличении числа наблюдений 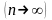вероятность неравенства 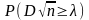стремится к пределу .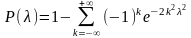

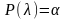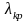Задавая уровень значимости , из соотношения по приведенной формуле рассчитаны и представлены в таблицах критические значения . Так, например, уровням значимости , равным 0,05, 0,01 и 0,001 соответствуют равные 1,36, 1,63 и 1,95 соответственно.