
- •Случайные события и их классификация.
- •Теорема сложения:
- •Теорема умножения :
- •Плотность распределения вероятностей и ее свойства.
- •Корреляционный момент и коэффициент корреляции и их свойства.
- •Моменты случайной величины. Ассиметрия и эксцесс.
- •Статистическая совокупность. Генеральная и выборочная совокупности. Несмещенная, состоятельная и эффективная оценка параметров.
- •Основные числовые характеристики статистического распределения. Среднее арифметическое и статистическая дисперсия и их свойства. Мода, медиана.
- •Выборочный метод. Точечное оценивание.
- •Интервальное оценивание. Формула доверительной вероятности для большой и малой выборок.
- •Несмещенные оценки для генерального среднего и генеральной дисперсии. Расчет доверительного интервала и объема выборки (при повторном и бесповторном отборах).
- •Статистическая проверка гипотез. Нулевая и альтернативная гипотезы. Ошибки 1-го и 2-го рода при проверки гипотез. Уровень значимости, критическая область. Критерии согласия и его мощность.
- •Проверка гипотезы о равенстве средних значении для нормального распределения при известной и неизвестной генеральной дисперсиях.
- •Критерий Пирсона.
- •Критерий согласия Фишера – Снедекора и его применение для проверки гипотезы о равенстве дисперсий.
- •Критерий согласия Колмогорова.
- •Однофакторный дисперсионный анализ.
- •Модели и основные понятия корреляционного и регрессионного анализа.
- •Линейная корреляционная зависимость и прямые регрессии.
- •Понятие «нелинейная корреляция».
- •Анализ соответствия регрессионной модели наблюденным данным.
Выборочный метод. Точечное оценивание.
Оценка неизвестного
параметра
генеральной совокупности одним
числом
называют точечной:
 =
.
=
.
Выборочная доля
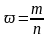 является
несмещенной и состоятельной оценкой
генеральной доли
является
несмещенной и состоятельной оценкой
генеральной доли
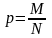 ,
дисперсия которой для повторной выборки
равна:
,
дисперсия которой для повторной выборки
равна:
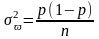 ,
а для бесповторной:
,
а для бесповторной:
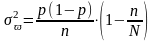
Выборочная средняя
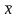 есть несмещенная и состоятельная оценка
генеральной средней
есть несмещенная и состоятельная оценка
генеральной средней
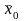 ,
дисперсия которой для повторной выборки
рана:
,
дисперсия которой для повторной выборки
рана:
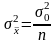 ,
а для бесповторной:
,
а для бесповторной: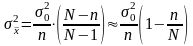 .
.
Выборочная дисперсия
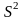 повторной
и бесповторной выборок есть смещенная
и состоятельная оценка генеральной
дисперсии
повторной
и бесповторной выборок есть смещенная
и состоятельная оценка генеральной
дисперсии
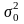 ,
так как
,
так как
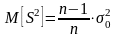 .
.
Не
смещенной и состоятельной оценкой
генеральной дисперсии
является исправленная выборочная
дисперсия
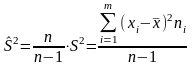 .
.
Интервальное оценивание. Формула доверительной вероятности для большой и малой выборок.
Интервальной
оценкой
параметра
называется
числовой интервал
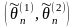 ,
который с заданной вероятностью
,
который с заданной вероятностью
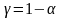 накрывает
неизвестной значение параметра
.
Такой интервал называют доверительным,
а вероятность
- доверительной
вероятностью
или надежностью
оценки.
накрывает
неизвестной значение параметра
.
Такой интервал называют доверительным,
а вероятность
- доверительной
вероятностью
или надежностью
оценки.
Наиболее часто
доверительный интервал выбирают
симметричным относительно параметра
:
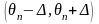 ,
где
,
где
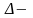 наибольшее
отклонение оценки
от параметра генеральной совокупности
,
возможное с вероятностью
и называется предельной
ошибкой выборки.
наибольшее
отклонение оценки
от параметра генеральной совокупности
,
возможное с вероятностью
и называется предельной
ошибкой выборки.
При заданной
доверительной вероятности
и большом объемы выборке, ее предельная
ошибка оценки генеральной средней и
генеральной доли равна
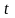 -кратной
величине средней квадратической ошибки
или средним квадратическим отклонениям
выборочной средней
-кратной
величине средней квадратической ошибки
или средним квадратическим отклонениям
выборочной средней
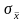 и
выборочной доли
и
выборочной доли
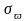 :
:
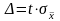 и
и
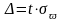 ,
,
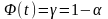 ,
где
,
где
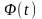 -функция
(интеграл вероятностей) Лапласа.
-функция
(интеграл вероятностей) Лапласа.
Интервальные
оценки (доверительные интервалы) для
генеральной средней и генеральной доли
равны:
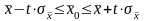 ;
;
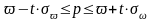 ,
где
и
в зависимости от типа отбора (повторный
или бесповторный) определяем по формулам:
,
где
и
в зависимости от типа отбора (повторный
или бесповторный) определяем по формулам:
Для повторного отбора:
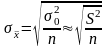 и
и
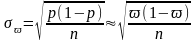 ;
;
Для бесповторного отбора:
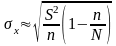 и
и
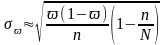 .
.
Несмещенные оценки для генерального среднего и генеральной дисперсии. Расчет доверительного интервала и объема выборки (при повторном и бесповторном отборах).
Выборочная средняя есть несмещенная и состоятельная оценка генеральной средней , дисперсия которой для повторной выборки рана: , а для бесповторной: .
Для определения
необходимого объема выборки
необходимо задать надежность (доверительную
вероятность)
оценки и точность (предельную ошибку
выборки)
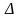 .
В этом случае необходимый объем выборки
для оценки генеральной средней
для повторного отбора находим по формуле:
.
В этом случае необходимый объем выборки
для оценки генеральной средней
для повторного отбора находим по формуле:
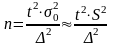 ,
и для бесповторного отбора:
,
и для бесповторного отбора:
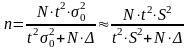 .
.
Интервальные оценки (доверительные интервалы) для генеральной средней и генеральной доли равны: ; , где и в зависимости от типа отбора (повторный или бесповторный) определяем по формулам:
Для повторного отбора:
и ;
Для бесповторного отбора:
и .
Статистическая проверка гипотез. Нулевая и альтернативная гипотезы. Ошибки 1-го и 2-го рода при проверки гипотез. Уровень значимости, критическая область. Критерии согласия и его мощность.
Статистической гипотезой называется любое предположение о виде или параметрах генеральной совокупности, проверяемое по выборке.
Проверяемую
гипотезу обычно называют нулевой
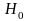 .
Наряду с
нулевой гипотезой
рассматривают
альтернативную,
или
конкурирующую,
гипотезу
.
Наряду с
нулевой гипотезой
рассматривают
альтернативную,
или
конкурирующую,
гипотезу
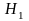 ,
являющуюся логическим отрицанием
.
,
являющуюся логическим отрицанием
.
Правило, по которому принимается или отвергается , называется статистическим критерием.
Вероятность отвергнуть гипотезу , при том, что она верна (т.е. принять гипотезу Н1), называется ошибкой 1 рода или уровнем значимости и обозначается α: P{H1/H0}=α.
Величина 1-α равна вероятности принять верную гипотезу и называется уровнем доверия: P{H0/H0}=1-α=γ.
Вероятность принять основную гипотезу, если она неверна, называется ошибкой 2 рода и обозначается β: P{H0/H1}=β.
Вероятность принять гипотезу Н1, если она верна, называется мощностью критерия: P{H1/H1}=1-β.
Область допустимых
значений
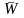 (область принятия гипотезы
);
(область принятия гипотезы
);
Критическая область
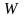 (область отбрасывания гипотезы
).
Она может быть:
(область отбрасывания гипотезы
).
Она может быть:
Правосторонняя, выбирается из соотношения:
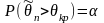 ;
;Левосторонняя:
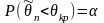 ;
;Двухсторонняя:
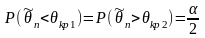 .
.
Одной из главных задач математической статистики является установление истинного закона распределения СВ на основании экспериментальных данных. На практике о виде закона распределения можно судить по графику выборочной плотности распределения вероятностей. Параметры закона распределения обычно неизвестны и их заменяют на выборочные значения. В соответствии с этим критерием, устанавливающие закон распределения, называются критериями согласия.
