29. Статистическая совокупность. Генеральная и выборочная совокупности. Несмещенная, состоятельная и эффективная оценка параметров.

Математическая статистика – раздел высшей математики, изучающий методы сбора, систематизации и обработки результатов случайных массовых явлений с целью выявления существующих закономерностей.

Вся подлежащая изучению совокупность объектов наблюдений называют генеральной совокупностью.

Та часть объектов, которая отобрана для непосредственного изучения из генеральной совокупности, называется выборочной совокупностью или выборкой. Число объектов в генеральной или в выборочной совокупности называют их объемом 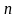. Основная форма представления выборочной совокупности – вариационные ряды. Вариационный ряд – это ранжированные в порядке возрастания или убывания ряд вариантов с соответствующими им весами (частотами и частостями). Выборка может быть повторная и бесповторная.

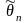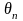Оценкой неизвестного параметра генеральной совокупности называют всякую функцию результатов наблюдений над случайной величиной 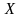, с помощью которой судят о значении параметра .

Оценка параметра называется несмещенной, если ее математическое ожидание равно оцениваемому параметру: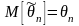 . Требование несмещенности гарантирует отсутствие систематических ошибок при оценивании.

Оценка параметра называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру:

или .

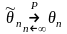Оценка параметра называется эффективной, если она имеет наименьшую дисперсию среди всех возможных оценок параметра , вычисленных по выборкам одного и того же объема .

30. Основные числовые характеристики статистического распределения. Среднее арифметическое и статистическая дисперсия и их свойства. Мода, медиана.

Эмпирическая функция распределения СВ Х равна частоте того, что Х примет значение меньшее, чем аргумент функции х и определяется формулой:

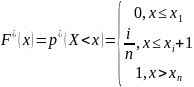
Для дискретного выборочного ряда средняя арифметическая равна: 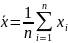, а для интервального ряда: 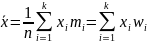(за xi принимают середину i-го интервала).

Дисперсия равна средней арифметической квадратов отклонений значений выборки от выборочного среднего: 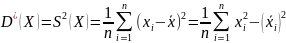. Исправленная дисперсия считается по выборке малого объема. В этом случае объем корректируется на 1:

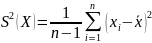
Медиана:

В дискретном ранжированном ряду медиана определяется:

- ряд с нечетным количеством элементов – медианой является элемент, стоящий в центре ряда;

- ряд с четным числом элементов – медианой является среднее значение 2 центральных элементов.

В интервальном ряду распределения медиана находится:

, где - нижняя граница медианного интервала, h – ширина медианного интервала, - сумма всех частот ряда, – сумма накопленных частот домедианного ряда, - частота медианного интервала.

Мода:

В дискретном стат ряду распределения моде соответствует элемент, который встречается чаще всего:

	3	7	12	18
	8	12	34	9

В интервальном ряду распределения мода вычисляется:

, где – нижняя граница модального интервала, h – ширина модального интервала, – частота модального интервала, - частота предмодального интервала, - частота постмодального интервала.

+Вариационный размах , равный разности между наибольшим и наименьшим вариантами ряда: .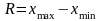

Среднее квадратическое отклонение : .

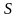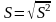Коэффициент вариаци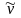и , равный процентному отношению среднего квадратического отклонения к средней арифметической: