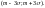Плотность распределения вероятностей и ее свойства.
СВ Х называется непрерывной, если ее функция распределения F(x) – непрерывная и дифференцируемая функция для всех значений аргумента.
Вероятность попадания НСВ Х на участок от х до х+△х = приращению функции распределения на этом участке: p(x<X<x+△x)=F(x+△x)-F(x).
Тогда плотность
вероятности на этом участке =
.
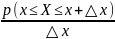При △x-> и переходя к пределу, получаем:
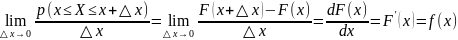
– плотность
распределения вероятности
Плотность распределения вероятности – функция, которая является 1 из форм закона распределения непрерывной СВ.
График плотности распределения называется кривой распределения.
Свойства f(x):
Плотность распределения неотрицательна f(x)≥0, т.к. ее первообразная F(x) является неубывающей функцией;
Условие нормировки:
;F(x)=
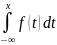;Вероятность попадания СВ в интервал (α;β): P(α<X<β)=
.
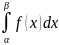Математическое ожидание дискретной и непрерывной случайной величины и их свойства.
Математическое ожидание М(х) – характеризует среднее значение случайной величины и вычисляется:
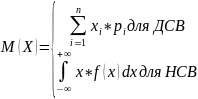
В качестве М(Х) используются средне взвешенные значения, при чем каждое из значений СВ учитывается с весом пропорциональным вероятности этого значения.
Физический смысл М(Х):
Среднее значение СВ, т.е. то значение, которое используется вместо СВ в приближенных расчетах.
Свойства М(Х):
М(С)=С
М(X+-Y)=M(X)+-M(Y)
M(C*X)=C*M(X)
Дисперсия случайной величины и ее свойства.
Дисперсия СВ характеризует степень рассеивания (разброса) значений СВ около ее математического ожидания и определяется по формулам:
Свойства Д(Х):
Д(С)=0
Д(С*Х)=С*C*Д(Х)
Д(X+-Y)= Д (X)+ Д (Y)
Дисперсия СВ имеет
размерность квадрата СВ, поэтому для
анализа диапазона значений СВ Х дисперсия
не совсем удобна. Для этого используется
средне квадратическое отклонение,
размерность которого совпадает с
размерностью СВ Х:
.
Биноминальный закон распределения. Математическое ожидание и дисперсия случайной, величины распределенной по биноминальному закону.
Биноминальным
называют закон распределения дискретной
случайной величины
-
числа появлений событий в
независимых испытаниях, в каждом из
которых вероятность появления события
равна
;
вероятность возможного значения
( числа
появлений события ) вычисляют по формуле
Бернулли :
,
где
.
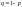При этом математическое ожидание и
дисперсия соответственно равны:
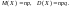
Условия возникновения: проводится n одинаковых независимых опытов, в каждом из которых событие А появляется с вероятностью р. СВ Х – число опытов, в которых произошло событие А.
Закон распределения Пуассона. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона.
Если число испытаний
велико, а вероятность появления события
в каждом испытании мала, то вероятность
того, что некоторое событие появиться
раз в
испытаниях, приближенно вычисляется
по формуле: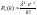
,
где
- число появлений событий в
независимых испытаниях,
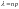- среднее число появлений событий в
испытаниях. Случайная величина,
характеризующая число наступлений
события
в
независимых испытаниях, распределена
по закону
Пуассона,
если
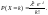
Математическое
ожидание и дисперсия случайной величины,
распределенной по закону Пуассона: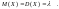
Условия возникновения:
применяется, когда число опытов n
неограниченно увеличивается, а вероятность
р наступления события А в 1 опыте ->0,
так что существует предел:
.
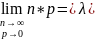Равномерный закон распределения. Математическое ожидание и дисперсия случайной величины, распределенной по равномерному закону.
Равномерное
распределение: Пусть
плотность вероятности равна нулю всюду,
кроме отрезка
,
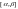на котором все значения случайной
величины Х одинаково возможны. Выражение
плотности распределения вероятностей
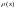имеет
следующий вид:
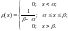
Функция
равномерного распределения задается
формулой:
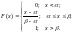
Математическое
ожидание, дисперсия и среднее квадратическое
отклонение соответственно равны:
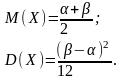
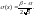
Показательный закон распределения. Математическое ожидание и дисперсия случайной величины, распределенной по показательному закону.
Показательное
распределение.
Показательным (экспоненциальным)
называют распределение вероятностей
непрерывной случайной величины
,
которое описывается функцией плотности
вероятности:
где
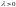постоянная и называется параметром
экспоненциального распределения.
Функция
распределения случайной величины,
распределенной по показательному
закону, имеет вид:
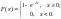
Математическое
ожидание
.
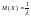Дисперсия
,
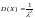среднее квадратическое отклонение
.
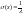Условия возникновения: СВ Х – интервал времени между 2 соседними событиями в простейшем или Пуассоновском процессе/потоке СС, λ – интенсивность потока.
Нормальный закон распределения. Математическое ожидание и дисперсия случайной величины, распределенной по нормальному закону.
Распределение с
непрерывной случайной величины называется
нормальным, если плотность распределения
ее описывается формулой: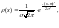
где
- параметры распределения.
Функция распределения случайной величины Х, распределенной по нормальному закону:
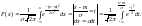
Полученный интеграл
нельзя выразить через элементарные
функции, но его можно вычислить через
специальную функцию:
,
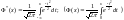называемую нормальной функцией
распределения (функцией Лапласа). Эта
функция неубывающая, непрерывная слева
и
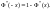
Математическое
ожидание и дисперсия соответственно
равны
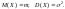
Выражение функции распределения нормальной величины через функцию Лапласа. Вероятность попадания значения нормальной случайной величины в заданный интервал, правило трех сигм.
Функция распределения случайной величины Х, распределенной по нормальному закону:
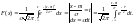
Полученный интеграл
нельзя выразить через элементарные
функции, но его можно вычислить через
специальную функцию:
,
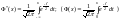называемую нормальной функцией
распределения (функцией Лапласа). Эта
функция неубывающая, непрерывная слева
и
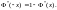
Вероятность
попадания случайной величины
,
подчиненной нормальному закону
распределения, на заданный интервал
,
определяется следующим образом:
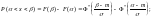или
функция Лапласа.
Вероятность заданного отклонения вычисляется по формуле:
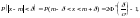или
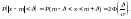
Интервалом
практически возможных значений случайной
величины
,
распределенной по нормальному закону,
будет интервал
