§ 139. Уравнения Максвелла для электромагнитного поля

Введение Максвеллом понятия тока смещения привело его к завершению созданной им макроскопической теории электромагнитного поля, позволившей с единой точки зрения не только объяснить электрические и магнитные явления, но и предсказать новые, существование которых было впоследствии подтверждено.

В основе теории Максвелла лежат рассмотренные выше четыре уравнения:

1. Электрическое поле (см. § 137) может быть как потенциальным (E_Q), так и вихревым (Е_в), поэтому напряженность суммарного поля Е = Е_е + Е_B. Так как циркуляция вектора E_Q равна нулю (см. (137.3)), а циркуляция вектора Е_в определяется выражением (137.2), то циркуляция вектора напряженности суммарного поля

Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.

2. Обобщенная теорема о циркуляции вектора Н (см. (138.4)):

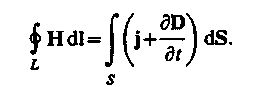
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущими ся зарядами (электрическими токами), либо переменными электрическими полями.

3. Теорема Гаусса для поля D (см. (89.3)):

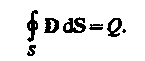(139.1)

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью , то формула (139.1) запишется в виде

4. Теорема Гаусса для поля В (см. (120.3)):

Итак, полная система уравнений Максвелла в интегральной форме:

Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):

где ₀ и ₀ — соответственно электрическая и магнитная постоянные,  и  — соответственно диэлектрическая и магнитная проницаемости,  — удельная проводимость вещества,

Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.

Для стационарных полей (E = const и В = const) уравнения Максвелла примут вид

т. е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного — только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.

Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса

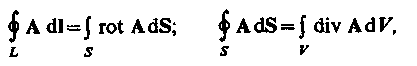
можно представить полную систему уравнений Максвелла в дифференциальной форме (характеризующих поле в каждой точке пространства):

Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла — интегральная и дифференциальная — эквивалентны. Однако если имеются поверхности разрыва — поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.

Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняют граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия. Они были рассмотрены раньше (см. § 90, 134):

(первое и последнее уравнения отвечают случаям, когда на границе раздела нет ни свободных зарядов, ни токов проводимости).

Уравнения Максвелла — наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т. е. электрическое и магнитное поля неразрывно связаны друг с другом — они образуют единое электромагнитное поле.

Теория Максвелла, являясь обобщением основных законов электрических и магнитных явлений, не только смогла объяснить уже известные экспериментальные факты, что также является важным ее следствием, но и предсказала новые явления. Одним из важных выводов этой теории явилось существование магнитного поля токов смещения (см. § 138), что позволило Максвеллу предсказать существование электромагнитных волн — переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью. В дальнейшем было доказано, что скорость распространения свободного электромагнитного поля (не связанного с зарядами и токами) в вакууме равна скорости света с = 310⁸ м/с. Этот вывод и теоретическое исследование свойств электромагнитных волн привели Максвелла к созданию электромагнитной теории света, согласно которой свет представляет собой также электромагнитные волны. Электромагнитные волны на опыте были получены немецким физиком Г. Герцем (1857—1894), доказавшим, что законы их возбуждения и распространения полностью описываются уравнениями Максвелла. Таким образом, теория Максвелла была экспериментально подтверждена.

К электромагнитному полю применим только принцип относительности Эйнштейна, так как факт распространения электромагнитных волн в вакууме во всех системах отсчета с одинаковой скоростью с не совместим с принципом относительности Галилея.

Согласно принципу относительности Эйнштейна, механические, оптические и электромагнитные явления во всех инерциальных системах отсчета протекают одинаково, т. е. описываются одинаковыми уравнениями. Уравнения Максвелла инвариантны относительно преобразований Лоренца: их вид не меняется при переходе от одной инерциальной системы отсчета к другой, хотя величины Е, В, D, Н в них преобразуются по определенным правилам.

Из принципа относительности вытекает, что отдельное рассмотрение электрического и магнитного полей имеет относительный смысл. Так, если электрическое поле создается системой неподвижных зарядов, то эти заряды, являясь неподвижными относительно одной инерциальной системы отсчета, движутся относительно другой и, следовательно, будут порождать не только электрическое, но и магнитное поле. Аналогично, неподвижный относительно одной инерциальной системы отсчета про водник с постоянным током, возбуждая в каждой точке пространства постоянное магнитное поле, движется относительно других инерциальиых систем, и создаваемое им переменное магнитное поле возбуждает вихревое электрическое поле.

Таким образом, теория Максвелла, ее экспериментальное подтверждение, а также принцип относительности Эйнштейна приводят к единой теории электрических, магнитных и оптических явлений, базирующейся на представлении об электромагнитном поле.

• Запишите полную систему уравнений Максвелла в интегральной и дифференциальной формах и объясните их физический смысл.

• Почему уравнения Максвелла в интегральной форме являются более общими?

• Почему постоянные электрические и магнитные поля можно рассматривать обособленно друг от друга? Запишите для них уравнения Максвелла в обеих формах.

 Какие основные выводы можно сделать на основе теории Максвелла?

КОЛЕБАНИЯ И ВОЛНЫ

Глава 18

Механические и

электромагнитные колебания

§ 140. Гармонические колебания и их

характеристики

Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебательные процессы широко распространены в природе и технике, например качание маятника часов, переменный электрический ток и т. д. При колебательном движении маятника изменяется координата его центра масс, в случае переменного тока колеблются напряжение и ток в цепи. Физическая природа колебаний может быть разной, поэтому различают колебания механические, электро магнитные и др. Однако различные колебательные процессы описываются одинаковы ми характеристиками и одинаковыми уравнениями. Отсюда следует целесообразность единого подхода к изучению колебаний различной физической природы. Например, единый подход к изучению механических и электромагнитных колебаний применялся английским физиком Д. У. Рэлеeм (1842—1919), А. Г. Столетовым, русским инженером-экспериментатором П. Н. Лебедевым (1866—1912). Большой вклад в развитие теории колебаний внесли Л. И. Мандельштам (1879—1944) и его ученики.

Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воз действий на колебательную систему (систему, совершающую колебания). Простейшим типом колебаний являются гармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Рассмотрение гармонических колебаний важно по двум причинам: 1) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому; 2) различные периодические процессы (процессы, повторяющиеся через равные промежутки времени) можно представить как наложение гармонических колебаний. Гармонические колебания величины s описываются уравнением типа

(140.1)

где А — максимальное значение колеблющейся величины, называемое амплитудой колебания, ₀ — круговая (циклическая) частота,  — начальная фаза колебания в момент времени t = 0, (₀t + ) — фаза колебания в момент времени t. Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до - 1, то s может принимать значения от + А до - А.

Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемый периодом колебания, за который фаза колебания получает приращение 2, т. е.

откуда

(140.2)

Величина, обратная периоду колебаний,

(140.3)

т. е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний. Сравнивая (140.2) и (140.3), получим

Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, при которой за 1 с совершается один цикл процесса.

Запишем первую и вторую производные по времени от гармонически колеблющейся величины s:

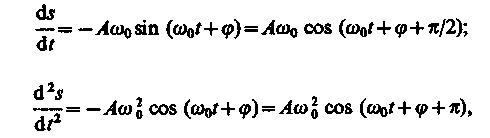(140.4) (140.5)

т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин (140.4) и (140.5) соответственно равны А₀ и А²₀. Фаза величины (140.4) отличается от фазы величины (140.1) на /2, а фаза величины (140.5) отличается от фазы величины (140.1) на . Следовательно, в моменты времени, когда s = 0, ds/dt приобретает наибольшие значения; когда же s достигает максимального отрицательного значения, то d²s/dt² приобретает наибольшее положительное значение (рис. 198).

Из выражения (140.5) следует дифференциальное уравнение гармонических колебаний

(140.6)

(где s = A cos (₀t + )). Решением этого уравнения является выражение (140.1).

Рис. 198

Гармонические колебания изображаются графически методом вращающегося вектора амплвтуды, или методом векторных диаграмм. Для этого из произвольной точки О, выбранной на оси х, под углом , равным начальной фазе колебания, откладывается вектор А, модуль которого равен амплитуде А рассматриваемого колебания (рис. 199).

Рис. 199

Если этот вектор привести во вращение с угловой скоростью ₀, равной циклической частоте колебаний, то проекция конца вектора будет перемещаться по оси х и принимать значения от - А до +А, а колеблющаяся величина будет изменяться со временем по закону s = Acos(w₀t + j). Таким образом, гармоническое колебание можно представить проекцией на некоторую произвольно выбранную ось вектора амплитуды А, отложенного из произвольной точки оси под углом , равным начальной фазе, и вращающегося с угловой скоростью ₀ вокруг этой точки.

В физике часто применяется другой метод, который отличается от метода вращающегося вектора амплитуды лишь по форме. В этом методе колеблющуюся величину представляют комплексным числом. Согласно формуле Эйлера, для комплексных чисел

где — мнимая единица. Поэтому уравнение гармонического колебания (140.1) можно записать в комплексной форме:

(140.8)

Вещественная часть выражения (140.8)

представляет собой гармоническое колебание. Обозначение Re вещественной части условимся опускать и (140.8) будем записывать в виде

В теории колебаний принимается, что колеблющаяся величина s равна вещественной части комплексного выражения, стоящего в этом равенстве справа.