Осевой момент инерции

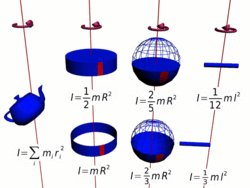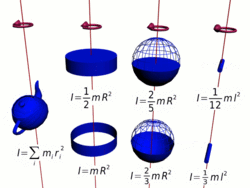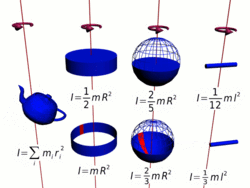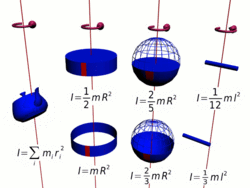
Осевые моменты инерции некоторых тел.

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех nматериальных точек системы на квадраты их расстояний до оси:

,

где:

• m_i — масса i-й точки,

• r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности впоступательном движении.

,

где:

• dm = ρdV — масса малого элемента объёма тела dV,

• ρ — плотность,

• r — расстояние от элемента dV до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

Теорема Штейнера

Вывод

Момент инерции, по определению:

Радиус-вектор   можно расписать как разность двух векторов:

,

где   — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:

Вынося за сумму  , получим:

Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:

Тогда:

Откуда и следует искомая формула:

,

где J_C — известный момент инерции относительно оси, проходящей через центр масс тела.

Уравнение динамики твёрдого тела, вращающегося вокруг неподвижной оси

Согласно уравнению (5.8 аналог второго закона Ньютона для вращательного движения, из которого следует, что угловое ускорение твердого тела при вращении вокруг неподвижной оси прямо пропорционально вращающему моменту и обратно пропорционально моменту инерции Относительно этой оси) второй закон Ньютона для вращательного движения

По определению угловое ускорение и тогда это уравнение можно

переписать следующим образом

с учетом (5.9 - Момент импульса тела относительно оси вращения)

или

(5.10)

Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела , равно импульсу момента всех внешних сил, действующих на это тело.

Плоское движение твердого тела. Уравнение динамики плоского движения.

Плоским называют такое движение тела, при котором все его точки движутся в плоскостях, параллельных заданной неподвижной. Проведем связанную с телом нормаль АА к заданной неподвижной плоскости и двигаясь вместе с телом, через промежуток времени dt нормаль занимает положение A1А1. Очевидно, что все точки тела, лежащие на этой нормали, движутся одинаково, в частности, так же, как и точка O пересечения нормали с сечением тела плоскостью, параллельной заданной неподвижной. То же можно сказать о точках тела, лежащих на любой другой нормали. Поэтому для изучения плоского движения тела достаточно рассмотреть движение его сечения плоскостью, параллельной заданной, т.е. ре      Таким образом, мы имеем следующие два уравнения, описывающие плоское движение твердого тела:

(6.34)

где т - масса тела,   - результирующая всех внешних сил,  и   - момент инерции и суммарный момент всех внешних сил относительно оси, проходящей через центр инерции тела.

шить задачу кинематики в плоской системе координат.

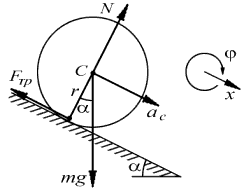
Пример. Однородный цилиндр массы m и радиуса r скатывается без скольжения по наклонной плоскости, составляющей угол   с (рис.6.18). Найти уравнения движения цилиндра.

Стандартный подход к решению подобной задачи состоит в следующем. Сперва определяют силы, действующие на тело, и точки их

Рис. 6.18.Скатывание цилиндра с наклонной плоскости

приложения. В данном случае это   - сила тяжести,  - нормальная составляющая силы реакции со стороны наклонной плоскости и   - сила трения покоя. Затем выберем положительные направления оси х и угла поворота  . Эти направления лучше всего взять сразу согласованными, так чтобы знаки ускорений  и   были одинаковы, например, как показано па рис.6.18, справа. После этого записывают сами уравнения движения, в проекциях па выбранные таким образом положительные направления  и  :

Кроме того, условие отсутствия скольжения определяет еще кинематическую связь между ускорениями:

Совместное решение этих трех уравнений дает возможность найти ускорения и   также силу  .

Работа внешних сил при вращении твердого тела.

Рассмотрим действие внешней силы  , приложенной к точке массой  . За время  элементарная масса   проходит путь   Работа силы   на этом пути определяется проекцией силы на направление перемещения, которая очевидно, равна тангенциальной составляющей   силы.

Но   равна модулю момента   силы   относительно оси вращения. Работа  , и будет положительна, если   имеет такое же направление, как и   отрицательное, если направление векторов   и   противоположны.

С учетом, что 

Работа всех сил, приложенных к телу

(5.13)

Полная работа

(5.14)

Уравнение гармонических колебаний и их основные характеристики.

Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:

x(t) = Asin(ωt + φ)

или

x(t) = Acos(ωt + φ),

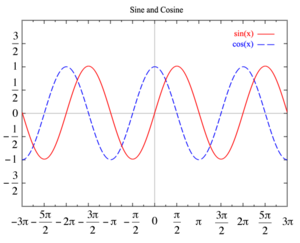
Графики функций f(x) = sin(x) и g(x) = cos(x) на декартовой плоскости.

где х — значение изменяющейся величины, t — время, остальные параметры - постоянные: А — амплитуда колебаний, ω — циклическая частота колебаний,(ωt + φ) — полная фаза колебаний,   — начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

(Любое нетривиальное^[1] решение этого дифференциального уравнения - есть гармоническое колебание с циклической частотой ω.)