Материальная точка. Твердое тело. Система отсчета и системы координат

Материа́льная то́чка — простейшая физическая модель в механике — математическая абстракция — тело, размеры которого допустимо считать бесконечно малыми по отношению к остальным объектам исследуемой задачи.

Практически под материальной точкой понимают обладающее массой тело, размерами и формой которого можно пренебречь при решении данной задачи.^[1] Например, при расчёте пути, пройденного поездом, можно пренебречь его размерами, даже если путь измеряется сантиметрами.

Механическая энергия может быть запасена материальной точкой лишь в виде кинетической энергии её движения в пространстве, и (или) потенциальной энергии взаимодействия с полем. Это автоматически означает неспособность материальной точки к деформациям (материальной точкой может быть названо лишь абсолютно твёрдое тело) и вращению вокруг собственной оси и изменениям направления этой оси в пространстве

Абсолю́тно твёрдое те́ло — второй опорный объект механики наряду с материальной точкой. Механика абсолютно твердого тела полностью сводима к механике материальных точек (с наложенными связями), но имеет собственное содержание (полезные понятия и соотношения, которые могут быть сформулированы в рамках модели абсолютно твердого тела), представляющее большой теоретический и практический интерес.

Существует несколько определений:

Абсолютно твёрдое тело — модельное понятие классической механики, обозначающее совокупность материальных точек, расстояния между которыми сохраняются в процессе любых движений, совершаемых этим телом. Иначе говоря, абсолютно твердое тело не только не изменяет свою форму, но и сохраняет неизменным распределение массы внутри.

Абсолютно твёрдое тело — механическая система, обладающая только поступательными и вращательными степенями свободы. «Твёрдость» означает, что тело не может быть деформировано, то есть телу нельзя передать никакой другой энергии, кроме кинетической энергии поступательного или вращательного движения.

Абсолютно твёрдое тело — тело (система), взаимное положение любых точек которого не изменяется, в каких бы процессах оно ни участвовало.

Таким образом, положение абсолютно твердого тела полностью определяется, например, положением жестко привязанной к нему декартовой системы координат (обычно ее начало координат делают совпадающим с центром масс твердого тела).

В трёхмерном пространстве и в случае отсутствия (других) связей абсолютно твёрдое тело обладает 6 степенями свободы: три поступательных и три вращательных. Исключение составляет двухатомная молекула или, на языке классической механики, твёрдый стержень нулевой толщины. Такая система имеет только две вращательных степени свободы.

Абсолютно твёрдых тел в природе не существует, однако в очень многих случаях, когда деформация тела мала и ей можно пренебречь, реальное тело может (приближенно) рассматриваться как абсолютно твёрдое тело без ущерба для задачи.

В рамках релятивистской механики понятие абсолютно твёрдого тела внутренне противоречиво, что показывает, в частности,парадокс Эренфеста. Другими словами, модель абсолютно твердого тела вообще говоря совершенно неприменима к случаю быстрых движений (сопоставимых по скорости со скоростью света), а также к случаю очень сильных гравитационных полей ^[1].

Система отсчёта — это совокупность точки отсчёта, системы координат и системы отсчёта времени, связанных с этой точкой, по отношению к которой изучается движение (или равновесие) каких-либо других материальных точек или тел^[1].

Математически движение тела (или материальной точки) по отношению к выбранной системе отсчёта описывается уравнениями, которые устанавливают, как изменяются с течением времени t координаты, определяющие положение тела (точки) в этой системе отсчёта. Эти уравнения называются уравнениями движения. Например, в декартовых координатах х, y, z движение точки определяется уравнениями x = f₁(t), y = f₂(t), z = f₃(t).

Прямоугольная, или Декартова система координат — наиболее простая и поэтому часто используемая система координат на плоскости и в пространстве.

Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей (что не является обязательным). OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат.

В полярной системе координат положение точки определяется расстояние до центра координат и углом радиус-вектора с осью Ox.

Термин «полярные координаты» используется только на плоскости, в пространстве применяются цилиндрические и сферические системы координат.

Кинематические характеристики движения: средние и мгновенные скорость и ускорение частицы, тангенциальное и нормальное ускорения.

Ско́рость (часто обозначается  , от англ. velocity или фр. vitesse) — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта (например, угловая скорость). Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.

Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора   этой точки:

Здесь   — модуль скорости,   — направленный вдоль скорости единичный вектор касательной к траектории в точке  .

Мгновенная и средняя скорость

Полезно отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден. В отличие от скорости перемещения, средняя скорость пути — скаляр.

Когда говорят о средней скорости , для различения, скорость согласно выше приведённому определению называют мгновенной скоростью. Так, хотя мгновенная скорость бегуна, кружащего по стадиону, в каждый момент времени отлична от нуля, его средняя скорость (перемещения) от старта до финиша оказывается равной нулю, если точки старта и финиша совпадают. Заметим, что при этом, средняя путевая скорость остаётся отличной от нуля.

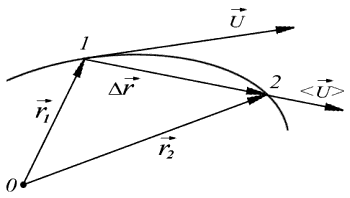
2.1. Кинематика частицы

Если размеры тела при описании его движения несущественны, то его движение можно рассматривать как движение частицы в пространстве. Это самая простая модель для описания реального тела. Так как в дальнейшем будут рассматриваться движения тела обладающего массой, но в пренебрежении ее размерами, внутренней структуры и формы, то введем в рассмотрение единый термин частица, понимая под ним материальную точку. Существует три способа описания движения частицы: векторный (геометрический), координатный и естественный. Рассмотрим их последовательно, учитывая, то аналогичное построение описания движения частицы будет применимо в релятивистском случае.

Векторный способ. В этом способе положение интересующей нас частицы А задают радиусом-вектором  , проведенным из некоторой неподвижной точки О выбранной системы отсчета в точку А. Под системой отсчета в механике понимают совокупность: тело отсчета, способ измерения расстояний ("линейка") и способ измерения времени ("часы"). При движении частицы А ее радиус-вектор меняется в общем случае как по модулю, так и по направлению, т. е. радиус-вектор   зависит от времени t.

Рис. 2.1. Векторный способ описания движения частицы

Геометрическое место точек, где тело побывало за время своего движения, называется траекторией частицы А. При векторном способе описания траекторией будет положение концов радиус-вектора   во все моменты времени.

Введем понятие скорости частицы. Скорость характеризует быстроту движения частицы. Пусть за промежуток времени   точка А переместилась из точки 1 в точку 2 (рис. 2.1). Из рисунка видно, что вектор перемещения   частицы А представляет собой приращение радиус-вектора  за время (t :  . Отношение   называют средним вектором скорости < > за время (t. Вектор < > совпадает по направлению с  . Определим теперь вектор скорости   частицы в данный момент времени как предел отношения   при (t® 0, т. е.

(2.1)

Это значит, что вектор скорости   частицы в данный момент времени равен производной от радиус-вектора   по времени и направлен по касательной к траектории в данной точке в сторону движения частицы А (как и вектор  ). Модуль вектора   равен

Заметим, что в общем случае модуль приращения радиус-вектора   не равен изменению модуля радиус-вектора  . Например, если   меняется только по направлению при движении частицы по окружности, то   но  .

Движение частицы характеризуется также ускорением. Вектор ускорения   определяет скорость изменения вектора скорости   со временем:

(2.2)

т. е. равен производной от вектора скорости по времени. Направление вектора   совпадает с направлением вектора   - приращением вектора   за время dt. Модуль вектора   определяется аналогично модулю вектора  . Пусть, например, радиус-вектор частицы зависит от времени t по закону

,

где   и  - постоянные векторы. Найдем скорость   и ускорение   частицы:   

Модуль вектора скорости

.

Таким образом, зная зависимость  , можно найти скорость   и ускорение   частицы в каждый момент времени.

Возникает и обратная задача: можно ли найти   и  , зная зависимость от времени ускорения  ?

Оказывается, для получения однозначного решения этой задачи одной зависимости   недостаточно, так как необходимо еще знатьначальные условия, а именно - скорость   и радиус-вектор   частицы в некоторый начальный момент  . Чтобы в этом убедиться, рассмотрим простой случай, когда при движении ускорение частицы   остается постоянным.

Определим сначала скорость частицы  . Согласно (2.2), за интервал времени dt малое приращение скорости  . Интегрируя это выражение по времени от t = 0 до t, определим конечное приращение вектора скорости за это время:

.

Но величина  - это еще не искомая скорость  . Для нахождения  , необходимо знать скорость   в начальный момент времени  . Тогда  , или

Аналогично вычисляется и радиус-вектор   частицы. Согласно (2.1), за интервал времени dt малое приращение радиус-вектора  . После интегрирования этого выражения с учетом определенной выше зависимости  , определим приращение радиуса-вектора за время от t = 0 до t:

.

Для нахождения самого радиус-вектора   необходимо знать положение частицы в начальный момент времени  . Тогда  ,

или

.

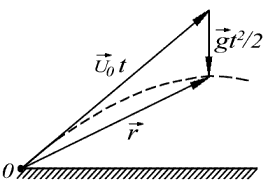
Рассмотрим в качестве примера движение камня, брошенного под некоторым углом к горизонту с начальной скоростью  . Если считать, что камень движется с постоянным ускорением  , то его положение относительно начальной точки движения ( ) определяется радиус-вектором

.

т. е. в этом случае

представляет собой сумму двух векторов, как показано на рис. 2.2.

.

Рис. 2.2. Суммирование векторов перемещения частицы

Для полного решения задачи о движении частицы - определения скорости   и положения   в зависимости от времени необходимо знать зависимость  (t) и начальные условия, т. е., скорость   и положение   частицы в начальный момент времени.

Координатный способ. В этом способе с телом отсчета жестко связывают определенную систему координат (декартову, косоугольную или криволинейную). Выбор вида системы координат определяется рядом соображений: характером или симметрией задачи, постановкой вопроса, а также стремлением упростить математическое решение задачи. Для простоты рассмотрим декартову систему координат x,у,z. Изучение движений частицы в других координатах оставим для задач.

Запишем проекции радиус-вектора   на оси координат. Вектор   определяет положение интересующей нас частицы относительно начала координат О в момент t:

Закон движения частицы - это зависимость координат от времени. Он задает положение частицы в каждый момент времени, ее скорость и ускорение. Cпроектировав (2.1) и (2.2), например, на OX, получим формулы, определяющие проекции векторов скорости и ускорения на эту ось:

,

(2.3)

где dx- проекция вектора перемещения   на ось х,

(2.4)

здесь   - проекция вектора приращения скорости   на ось х. Такие же соотношения получаются для у- и z-проекций соответствующих векторов. Из этих формул видно, что проекции векторов скорости и ускорения равны соответственно первой и второй производным координат по времени.

Зависимости   полностью определяют движение частицы. Зная их, можно найти не только положение частицы, но и проекции ее скорости и ускорения, а следовательно, модуль и направление векторов   и   в любой момент времени. Например, модуль вектора скорости определяется формулой

,

а направление вектора   задается направляющими косинyсами по формулам:

(2.5)

где (, ( ,( - углы между вектором   и осями х, у, z соответственно. Направляющие косинусы всегда удовлетворяют соотношению  . Аналогичными формулами определяются модуль и направление вектора ускорения  .

С помощью закона движения можно найти траекторию частицы, зависимость пройденного ею пути от времени, зависимость скорости от положения частицы и т.д.

Нахождение скорости и закона движения частицы по заданному ускорению называется обратной задачей. Ее решение проводится, как и в векторном способе, путем интегрирования (в данном случае проекций ускорения по времени). Задача и здесь имеет однозначное решение, если кроме ускорения заданы еще и начальные условия: проекции скорости и координаты частицы в начальный момент времени.

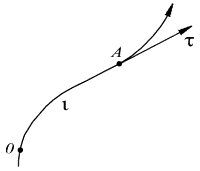
Естественный способ. Его применяют в том случае, когда заранее известна траектория частицы. Положение движущегося тела определяют дуговой координатой l - расстоянием вдоль траектории от выбранного начала отсчета точки О (рис. 2.3).

Рис. 2.3. Естественный способ описания движения

При этом произвольно выбирают положительное направление отсчета координаты l (например, как показано стрелкой на рисунке 2.3).

Движение частицы задано полностью, если определена ее траектория, начало отсчета О, положительное направление отсчета дуговой координаты l и закон движения частицы, т. е. зависимость  .

Рассмотрим как в этом способе описания определяется скорость частицы. Введем единичный вектор  , связанный с движущейся точкой А и направленный по касательной к траектории в сторону увеличения дуговой координаты l (рис. 2.3). Ясно, что   - переменный вектор: его направление зависит от l, хотя длина этого вектора остается неизменной. Вектор скорости   частицы А направлен по касательной к траектории, поэтому его можно выразить так:

(2.6)

где   - проекция вектора   на направление вектора  , причем  - величина алгебраическая. Кроме того, ясно, что

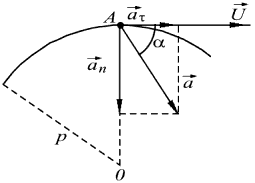
Рассмотрим теперь ускорение частицы  . Продифференцируем (2.6) по времени:

Преобразуем последнее слагаемое этого выражения:

(2.7)

Рассмотрим приращение вектор  на участке dl (рис. 2.4).

Рис. 2.4. Определение радиуса кривизны траектории

Можно строго показать, что при стремлении точки 2 к точке 1 отрезок траектории между ними можно представить в виде дуги окружности с центром в некоторой точке О. Ее называют центром кривизны траектории в данной точке, а радиус R соответствующей окружности - радиусом кривизны траектории в той же точке.

Как видно из рис. 2.4, угол  , откуда  , причем при  . Если ввести единичный вектор нормали   к траектории в точке 1, направленный к центру кривизны, то последнее равенство запишется в векторном виде:

(2.8)

Подставляя (2.8) в (2.7), а затем полученное выражение - в (2.6), получим в итоге выражение для вектора ускорения 

(2.9)

Здесь первое слагаемое называют тангенциальным ускорением  , а второе - нормальным (центростремительным) 

(2.10)

В итоге полное ускорение   может быть представлено как сумма тангенциального   и нормального   ускорений.

Модуль полного ускорения вычисляется по теореме Пифагора

Точка А движется по дуге окружности радиусом R (рис. 2.5).

Рис. 2.5. Определение полного ускорения частицы

Ее скорость зависит от дуговой координаты l но закону   где постоянная (определите эту константу самостоятельно). Найдем угол ( между векторами полного ускорения и скорости частицы как функцию координаты l.

Из рис. 2.5 видно, что угол ( можно определить из соотношения составляющих полного ускорения по формуле  . Значения компонент вектора полного ускорения   и  . Вычисляются по формулам:

Отсюда получаем  .

Вращение твердого тела вокруг неподвижной оси. Средние и мгновенные угловые скорость и ускорение.

Враще́ние — круговое движение объекта. В плоском пространстве объект вращается вокруг центра (илиточки) вращения. В трёхмерном пространстве объект вращается вокруг линии, называемой осью. Если ось вращения расположена внутри тела, то говорят, что тело вращается само по себе или обладает спином, который имеет относительную скорость и может иметь момент импульса. Круговое движение относительно внешней точки, например, вращение Земли вокруг Солнца, называется орбитальным движением или, более точно,орбитальным вращением.

При равномерном вращении (T оборотов в секунду),

Частота вращения — число оборотов тела в единицу времени. ,

Период вращения — время одного полного оборота. Период вращения T и его частота ν связаны соотношением T = 1 / ν.

Линейная скорость точки, находящейся на расстоянии R от оси вращения ,

Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величинаJ_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

где: m_i — масса i-й точки, r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как массатела является мерой его инертности в поступательном движении.

Кинетическая энергия вращательного движения

где I_z — момент инерции тела относительно оси вращения. ω — угловая скорость

Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

,

а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходныхпаровых машин определяли, просто «вручную» подсчитывая число оборотов за единицу времени.

Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью   определяется формулой:

где   — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) r от оси вращения можно считать так: v = rω. Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.

Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.

При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно^[1]:

Вектор углового ускорения α направлен вдоль оси вращения (в сторону   при ускоренном вращении и противоположно   — при замедленном).

При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости ω по времени^[2], то есть

,

и направлен по касательной к годографу вектора   в соответствующей его точке.

Существует связь между тангенциальным и угловым ускорениями:

,

где R — радиус кривизны траектории точки в данный момент времени. Итак, угловое ускорение равно второй производной от угла поворота по времени или первой производной от угловой скорости по времени. Угловое ускорение измеряется в рад/сек² .

Первый закон Ньютона и инерциальная система отсчета.

Первый закон Ньютона

Первый закон механики, или закон инерции (инерция – это свойство тел сохранять свою скорость при отсутствии действия на него других тел), как его часто называют, был установлен еще Галилеем. Но строгую формулировку этого закона дал и включил его в число основных законов механики Ньютон. Закон инерции относится к самому простому случаю движения – движению тела,на которое не оказывают воздействия другие тела. Такие тела называются свободными телами.

Ответить на вопрос, как движутся свободные тела, не обращаясь к опыту,нельзя. Однако нельзя поставить ни одного опыта, который бы в чистом виде показал, как движется ни с чем не взаимодействующее тело, так как таких тел нет. Как же быть?

Имеется лишь один выход. Надо создать для тела условия, при которых влияние внешних воздействий можно делать все меньшим и меньшим, и наблюдать, к чемуэто ведет. Можно, например, наблюдать за движением гладкого камняна горизонтальной поверхности, после того как ему сообщена некоторая скорость. (Притяжение камня к земле уравновешивается действием поверхности,на которую он опирается, и на скорость его движения влияет только трение.) При этом легко обнаружить, что чем более гладкой является поверхность, тем медленнее будет уменьшаться скорость камня. На гладком льду камень скользит весьма долго, заметно не меняя скорость. Трение можно уменьшить до минимумас помощью воздушной подушки – струй воздуха, поддерживающих тело над твердой поверхностью, вдоль которой происходит движение. Этот принциписпользуется в водном транспорте (суда на воздушной подушке). На основеподобных наблюдений можно заключить: если бы поверхность была идеально гладкой, то при отсутствии сопротивления воздуха (в вакууме) камень совсемне менял бы своей скорости. Именно к такому выводу впервые пришел Галилей.

С другой стороны, нетрудно заметить, что, когда скорость тела меняется, всегда обнаруживается воздействие на него других тел. Отсюда можно прийти к выводу,что тело, достаточно удаленное от других тел и по этой причинене взаимодействующее с ними, движется с постоянной скоростью.

Движение относительно, поэтому имеет смысл говорить лишь о движении тела по отношению к системе отсчета, связанной с другим телом. Сразу же возникает вопрос: будет ли свободное тело двигаться с постоянной скоростью по отношению к любому другому телу? Ответ, конечно, отрицательный. Так, если по отношению к Земле свободное тело движется прямолинейно и равномерно, то по отношению к вращающейся карусели тело заведомо так двигаться не будет.

Наблюдения за движениями тел и размышления о характере этих движений приводят нас к заключению о том, что свободные тела движутся с постояннойскоростью, по крайней мере, по отношению к определенным телам и связаннымс ними системам отсчета. Например, по отношению к Земле. В этом состоит главное содержание закона инерции.

Поэтому первый закон Ньютона может быть сформулирован так:

существуют такие системы отсчета, относительно которых тело (материальная точка) при отсутствии на неё внешних воздействий (или при их взаимнойкомпенсации) сохраняет состояние покоя или равномерного прямолинейного движения.

Инерциальная система отсчета

Первый закон Ньютона утверждает (которое с той или иной степенью точности можно проверить на опыте) о том, что инерциальные системы существуютв действительности. Этот закон механики ставит в особое, привилегированное положение инерциальные системы отсчета.

Системы отсчета, в которых выполняется первый закон Ньютона, называютинерциальными.

Или

Инерциальные системы отсчета – это системы, относительно которых материальная точка при отсутствии на нее внешних воздействий или их взаимнойкомпенсации покоится или движется равномерно и прямолинейно.

Инерциальных систем существует бесконечное множество. Система отсчета, связанная с поездом, идущим с постоянной скоростью по прямолинейному участку пути, – тоже инерциальная система (приближенно), как и система,связанная с Землей. Все инерциальные системы отсчета образуют класс систем, которые движутся друг относительно друга равномерно и прямолинейно.Ускорения какого-либо тела в разных инерциальных системах одинаковы.

Как установить, что данная система отсчета является инерциальной? Это можносделать только опытным путем. Наблюдения показывают, что с очень высокой степенью точности можно считать инерциальной системой отсчетагелиоцентрическую систему, у которой начало координат связано с Солнцем,а оси направлены на определенные «неподвижные» звезды. Системы отсчета, жестко связанные с поверхностью Земли, строго говоря, не являютсяинерциальными, так как Земля движется по орбите вокруг Солнца и при этом вращается вокруг своей оси. Однако при описании движений, не имеющихглобального (т. е. всемирного) масштаба, системы отсчета, связанные с Землей,можно с достаточной точностью считать инерциальными.

С гораздо большей точностью можно считать инерциальной систему отсчета,в которой начало координат совмещено с центром Солнца, а координатные оси направлены к неподвижным звездам. Эту систему отсчета называют гелиоцентрической.

Инерциальными являются и системы отсчета, которые движутся равномернои прямолинейно относительно какой-либо инерциальной системы отсчета.

Галилей установил, что никакими механическими опытами, поставленными внутри инерциальной системы отсчета, невозможно установить, покоится эта система или движется равномерно и прямолинейно. Это утверждение носит названиепринципа относительности Галилея или механического принципа относительности.

Этот принцип был впоследствии развит А. Эйнштейном и является однимиз постулатов специальной теории относительности. Инерциальные системы отсчета играют в физике исключительно важную роль, так как, согласнопринципу относительности Эйнштейна, математическое выражение любою закона физики имеет одинаковый вид в каждой инерциальной системе отсчета.В дальнейшем мы будем пользоваться только инерциальными системами(не упоминая об этом каждый раз).

Системы отсчета, в которых первый закон Ньютона не выполняется, называютнеинерциальными.

К таким системам относится любая система отсчета, движущаяся с ускорениемотносительно инерциальной системы отсчета.

В механике Ньютона законы взаимодействия тел формулируются для класса инерциальных систем отсчета.

Примером механического эксперимента, в котором проявляется неинерциальность системы, связанной с Землей, служит поведение маятника Фуко. Так называетсямассивный шар, подвешенный на достаточно длинной нити и совершающий малые колебания около положения равновесия. Если бы система, связанная с Землей,была инерциальной, плоскость качаний маятника Фуко оставалась бы неизменной относительно Земли. На самом деле плоскость качаний маятника вследствие вращения Земли поворачивается, и проекция траектории маятникана поверхность Земли имеет вид розетки (рис. 1).

Рис. 1.

О том, что телу свойственно сохранять не любое движение, а именнопрямолинейное, свидетельствует, например, следующий опыт (рис. 2). Шарик, двигавшийся прямолинейно по плоской горизонтальной поверхности, сталкиваясьс преградой, имеющей криволинейную форму, под действием этой преграды вынужден двигаться по дуге. Однако когда шарик доходит до края преграды,он перестает двигаться криволинейно и вновь начинает двигаться по прямой. Обобщая результаты упомянутых (и аналогичных им) наблюдений, можно сделать вывод, что если на данное тело не действуют другие тела или их действиявзаимно компенсируются, это тело покоится или же скорость его движенияостается неизменной относительно системы отсчета, неподвижно связанной споверхностью Земли.

Масса и импульс. Второй закон Ньютона как уравнение движения.

И́мпульс (Количество движения) — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этой точки на её скорость v, направление импульса совпадает с направлением вектора скорости: .

Инертная масса, которая характеризует меру инертности тел и фигурирует в одной из формулировок второго закона Ньютона. Если произвольная сила в инерциальной системе отсчёта одинаково ускоряет разные исходно неподвижные тела, этим телам приписывают одинаковую инертную массу.

Второй закон Ньютона — дифференциальный закон движения, описывающий зависимость ускорения тела от равнодействующей всех приложенных к телу сил. Один из трёх законов Ньютона.

Второй закон Ньютона в его наиболее распространённой формулировке утверждает: в инерциальных системах ускорение, приобретаемое материальной точкой (телом), прямо пропорционально вызывающей его силе, совпадает с ней по направлению иобратно пропорционально массе материальной точки (тела).

В приведённой формулировке второй закон Ньютона справедлив только для скоростей, много меньших скорости света и винерциальных системах отсчёта.

[править]Формулировки

В своих трудах «Математические начала натуральной философии», Исаак Ньютон приводит следующую формулировку своего закона^[1]

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

«Школьная формулировка»: в инерциальных системах ускорение, приобретаемое материальной точкой (телом), прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки (тела).

Обычно этот закон записывается в виде формулы:

,

где   — ускорение тела,   — сила, приложенная к телу, а   — масса тела, причём   — константа.

Или, в более известном виде:

Формулировка второго закона Ньютона, пригодная в случае тел переменной массы:

В инерциальной системе отсчета производная импульса материальной точки по времени равна действующей на него силе^[2].

где   — импульс (количество движения) тела,   — время, а   — производная по времени.

Уравнения, соответствующие данному закону, называются уравнениями движения материальной точки.

Применимость различных формулировок

Второй закон Ньютона в виде   приближённо справедлив только для скоростей, много меньших скорости света и винерциальных системах отсчёта. В виде   второй закон Ньютона точно справедлив также в инерциальных системах отсчёта специальной теории относительности и в локально инерциальных системах отсчёта общей теории относительности.

Третий закон Ньютона.

Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой  , а второе — на первое с силой  . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.

Современная формулировка

Материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами.

Историческая формулировка

Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга равны и направлены в противоположные стороны.

Закон всемирного тяготения. Сила тяжести и вес. Упругие силы. Силы реакции, силы сухого и вязкого трения.

В рамках классической механики гравитационное взаимодействие описывается законом всемирного тяготения. Этот закон был открыт Ньютоном в 1666 г.. Он гласит, что сила гравитационного притяжения между двумя материальными точками массы m₁ и m₂, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть:

Здесь G — гравитационная постоянная, равная   м³/(кг с²).

СИЛА ТЯЖЕСТИ, сила P, действующая на любое тело, находящееся вблизи земной поверхности, и определяемая как геометрическая сумма силы притяжения Земли F и центробежной силы инерции Q, учитывающей эффект суточного вращения Земли. Направление силы тяжести - вертикаль в данной точке земной поверхности. Аналогично определяется сила тяжести на любом небесном теле. Значение силы тяжести зависит от географической широты положения тела; например, на Земле сила тяжести на полюсе и на экваторе отличаются на 0,5% (на Луне значения силы тяжести примерно в 6 раз меньше, чем на Земле; смотри Ускорение свободного падения).

Частным видом силы всемирного тяготения является сила притяжения тел к Земле (или к другой планете). Эту силу называют силой тяжести. Под действием этой силы все тела приобретают ускорение свободного падения. В соответствии со вторым законом Ньютона g = Ft*m следовательно, Ft = mg. Сила тяжести всегда направлена к центру Земли. В зависимости от высоты h над поверхностью Земли и географической широты положения тела ускорение свободного падения приобретает различные значения. На поверхности Земли и в средних широтах ускорение свободного падения равно 9,831 м/с2.          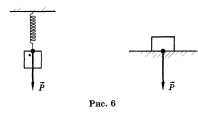В технике и быту широко используется понятие веса тела. Весом тела называют силу, с которой тело давит на опору или подвес в результате гравитационного притяжения к планете (рис. 6). Вес тела обозначается Р. Единица веса — Н. Так как вес равен силе, с которой тело действует на опору, то в соответствии с третьим законом Ньютона по величине вес тела равен силе реакции опоры. Поэтому, чтобы найти вес тела, необходимо определить, чему равна сила реакции опоры.                       Рассмотрим случай, когда тело вместе с опорой не движется. В этом случае сила реакции опоры, а следовательно, и вес тела равен силе тяжести (рис. 7):                    Р = N = mg.          В случае движения тела вертикально вверх вместе с опорой с ускорением по второму закону Ньютона можно записать mg + N = та (рис. 8, а).          В проекции на ось OX: -mg + N = та, отсюда N = m(g + a).          Следовательно, при движении вертикально вверх с ускорением вес тела увеличивается и находится по формуле Р = m(g + a).          Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называют перегрузкой. Действие перегрузки испытывают на себе космонавты как при взлете космической ракеты, так и при торможении корабля при входе в плотные слои атмосферы. Испытывают перегрузки и летчики при выполнении фигур высшего пилотажа, и водители автомобилей при резком торможении.          Если тело движется вниз по вертикали, то с помощью аналогичных рассуждений получаем  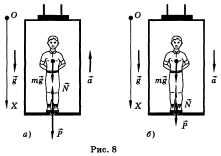                         т. е. вес при движении по вертикали с ускорением будет-меньше силы тяжести (рис. 8, б).          Если тело свободно падает, то в этом случае P = (g- g)m = 0.  2. Упругие силы. Сила, вызванная деформацией тел и препятствующая изменению объема тела, называется силой упругости.

Деформация называется упругой, если после снятия внешнего воздействия тело возвращается в исходное состояние. При небольших деформациях растяжения или сжатия х сила  упругости прямо пропорциональна деформации и направлена в сторону противоположную ей. Fупр = – kx, где k – коэффициент упругости, зависящий от свойств материала и геометрии деформируемого тела. Сила упругости препятствует деформации. Для характеристики упругих свойств вещества вводиться величина E, называемая модулем Юнга. Напряжение σ, возникающие в твердом теле, равно σ=F/S, где S площадь поперечного сечения твердого тела, на которое воздействует сила F. Относительная деформация ε=x/l0, где l0 – длина тела до деформации пропорциональна напряжению, возникающему в твёрдом теле (закон Гука). ε=(1/E)σ. Физический смысл модуля Юнга состоит в следующем: величина E численно равна напряжению, возникшему в твердом теле при относительной деформации, равной единице. Из физического смысла модуля Юнга следует, что E является большим по величине.

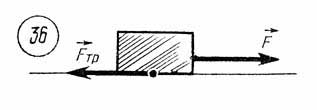
3. Силы трения. Силы трения покоя. Прикрепим к бруску крючок динамометра и попытаемся привести брусок в движение. Растяжение пружины динамометра показывает, что на брусок действует сила упругости, но тем не менее брусок остается неподвижным. Это значит, что при действии на брусок силы упругости в направлении, параллельном поверхности соприкосновения бруска со столом, возникает равная ей по модулю сила противоположного направления. Сила, возникающая на границе соприкосновения тел при отсутствии относительного движения тел, называетсясилой трения покоя.

Сила трения покоя   равна по модулю внешней силе  , направленной по касательной к поверхности соприкосновения тел, и противоположна ей по направлению (рис. 36):

.

Сила трения скольжения. Прикрепим динамометр к бруску и заставим брусок двигаться равномерно по горизонтальной поверхности стола. Во время равномерного движения бруска динамометр показывает, что на брусок со стороны пружины действует постоянная сила упругости  . При равномерном движении бруска равнодействующая всех сил, приложенных к нему, равна нулю. Следовательно, кроме силы упругости, во время равномерного движения на брусок действует сила, равная по модулю силе упругости, но направленная в противоположную сторону. Эта сила называется силой трения скольжения  .

Вектор силы трения скольжения   всегда направлен противоположно вектору скорости   движения тела относительно соприкасающегося с ним тела. Поэтому действие силы трения скольжения всегда приводит к уменьшению модуля относительной скорости тел.

Природа силы трения. Силы трения возникают благодаря существованию сил взаимодействия между молекулами и атомами соприкасающихся тел. Последние обусловлены взаимодействием электрических зарядов, которыми обладают частицы, входящие в состав атомов.

Коэффициент трения. Исследуем, от чего зависит сила трения. Для этого воспользуемся гладкой деревянной доской, деревянным бруском и динамометром (рис. 37).

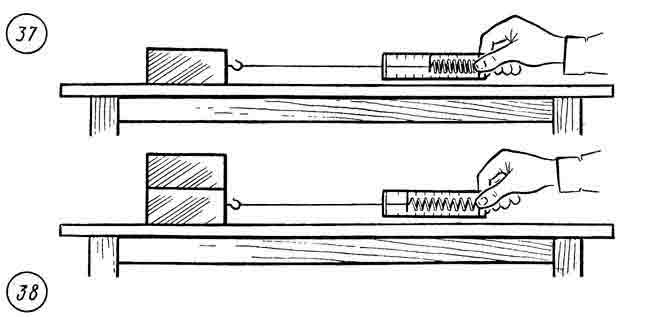
Сначала проверим, зависит ли сила трения от площади поверхности соприкосновения тел. Положим брусок на горизонтально расположенную доску гранью с самой большой площадью поверхности. Прикрепив к бруску динамометр, будем плавно увеличивать силу, направленную вдоль поверхности доски, и заметим максимальное значение силы трения покоя. Затем поставим тот же брусок на другую грань с меньшей площадью поверхности и вновь измерим максимальное значение силы трения покоя. Опыт показывает, что максимальное значение силы трения покоя не зависит от площади поверхности соприкосновения тел.

Повторив такие же измерения при равномерном движении бруска по поверхности доски, убеждаемся, что сила трения скольжения также не зависит от площади поверхности соприкосновения тел.

Поставим на первый брусок второй такой же. Этим мы увеличим силу, перпендикулярную поверхности соприкосновения тела и стола (ее называют силой давления  ). Если теперь мы вновь измерим максимальную силу трения покоя (рис. 38), то увидим, что она увеличилась в два раза. Поставив на два бруска третий, обнаруживаем, что максимальная сила трения покоя увеличилась в три раза.

На основании таких опытов можно сделать вывод, что максимальное значение модуля силы трения покоя прямо пропорционально силе давления.

Взаимодействие тела и опоры вызывает деформацию и тела, и опоры.

Силу упругости  , возникающую в результате деформации опоры и действующую на тело, называют силой реакции опоры (рис. 39).

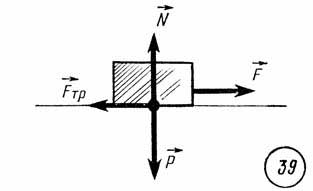
По третьему закону Ньютона сила давления и сила реакции опоры равны по модулю и противоположны по направлению:

.

Поэтому предыдущий вывод можно сформулировать так: модуль максимальной силы трения покоя пропорционален силе реакции опоры:

.

Греческой буквой   обозначен коэффициент пропорциональности, называемый коэффициентом трения.

Опыт показывает, что модуль силы трения скольжения  , как и модуль максимальной силы трения покоя, пропорционален модулю силы реакции опоры:

.

Максимальное значение силы трения покоя примерно равно силе трения скольжения, приближенно равны также коэффициенты трения покоя и скольжения.

Силы трения возникают и при качении тела. При одинаковой нагрузке сила трения качения значительно меньше силы трения скольжения. Поэтому для уменьшения сил трения в технике применяются колеса, шариковые и роликовые подшипники.

Система материальных точек. Внутренние и внешние силы. Основное уравнение динамики для системы частиц.

Система материальных точек или механическая система – Совокупность материальных точек или материальных тех, объединяемых общими законами взаимодействия (положение или движение каждой из точек или тела зависит от положения и движения всех остальных)

Для точки   уравнение движения относител  В механике внешними силами по отношению к данной системе материальных точек (т. е. такой совокупности материальных точек, в которой движение каждой точки зависит от положений или движений всех остальных точек) называются те силы, к-рые представляют собою действие на эту систему других тел (других систем материальных точек), не включенных нами в состав данной системы. Внутренними силами являются силы взаимодействия между отдельными материальными точками данной системы. Подразделение сил на внешние и внутренние является совершенно условным: при изменении заданного состава системы некоторые силы, ранее бывшие внешними, могут стать внутренними, и обратно. Так, например, при рассмотрении

движения системы, состоящей из земли и ее спутника луны, силы взаимодействия между этими телами будут внутренними силами для этой системы, а силы притяжения солнца, остальных планет, их спутников и всех звезд будут внешними силами по отношению к указанной системе. Но если изменить состав системы и рассматривать движение солнца и всех планет как движение одной общей системы, то внешн. силами будут только силы притяжений, оказываемых звездами; все же силы взаимодействия между планетами, их спутниками и солнцем становятся для этой системы силами внутренними. Точно так же, если при движении паровоза выделим поршень парового цилиндра как отдельную систему материальных точек, подлежащую нашему рассмотрению, то давление пара на поршень по отношению к нему явится внешней силой, и то же давление пара будет одной из внутренних сил, если будем рассматривать движение всего паровоза в целом; в этом случае внешними силами по отношению ко всему паровозу, принятому за одну систему, будут: трение между рельсами и колесами паровоза, сила тяжести паровоза, реакция рельсов и сопротивление воздуха; внутренними силами будут все силы взаимодействия между частями паровоза, напр. силы взаимодействия между паром и поршнем цилиндра, между ползуном и его параллелями , между шатуном и пальцем кривошипа, и т. п. Как видим, по существу нет различия между внешними и внутренними силами, относительное же различие между ними определяется лишь в зависимости от того, какие тела мы включаем в рассматриваемую систему и какие считаем не входящими в состав системы.

Относительно инерциальной системы отсчёта:

Закон сохранения импульса для системы частиц.

Перепишем его для системы из N частиц:

где суммирование идет по всем силам, действующим на n-ю частицу со стороны m-ой. Согласно третьему закону Ньютона, силы вида   и   будут равны по абсолютному значению и противоположны по направлению, то есть   Тогда после подстановки полученного результата в выражение (1) правая часть будет равна нулю, то есть:

или

Как известно, если производная от некоторого выражения равна нулю, то это выражение есть постоянная величина относительно переменной дифференцирования, а значит:

(постоянный вектор).

То есть суммарный импульс системы частиц есть величина постоянная. Нетрудно получить аналогичное выражение для одной частицы.

Следует учесть, что вышеприведенные рассуждения справедливы лишь для замкнутой системы.

Также стоит подчеркнуть, что изменение импульса   зависит не только от действующей на тело силы, но и от продолжительности её действия.

Центр масс. Уравнение движения центра масс. Система центра масс.

Центр масс (центр ине́рции; барице́нтр от др.-греч. βαρύς «тяжёлый» и κέντρον «центр») в механике — это геометрическая точка, характеризующая движение тела или системы частиц как целого.

Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом:

где

— радиус-вектор центра масс,

— радиус-вектор i-й точки системы,

— масса i-й точки.

Для случая непрерывного распределения масс:

где:

— суммарная масса системы,

— объём,

— плотность.

.

Уравнение движения центра масс

Систе́ма це́нтра масс (систе́ма це́нтра ине́рции) — невращающаяся система отсчёта, связанная с центром масс механической системы. Обычно сокращается как с. ц. м. или с. ц. и. Суммарный импульс системы в с.ц.м. равен нулю. Для замкнутой системы её система центра масс инерциальна, тогда как незамкнутая система в общем случае может обладать неинерциальной системой центра масс. Суммарная кинетическая энергия механической системы в с.ц.м. минимальна среди всех систем отсчёта; в любой другой невращающейся (не обязательно инерциальной) системе отсчёта кинетическая энергия равна кинетической энергии в с.ц.м. плюс кинетическая энергия движения механической системы как целого (MV²/2, где М — полная масса механической системы, V — относительная скорость движения систем отсчёта).

Работа переменной силы. Мощность. Кинетическая энергия частицы и системы частиц. Теорема Кенига.

Работа равна сумме работ(адитивная величина)

Аддитивность (лат. additivus — прибавляемый) — свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям, в некотором классе возможных разбиений объекта на части. Например, аддитивность объёма означает, что объём целого тела равен сумме объёмов составляющих его часте

Мо́щность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

средняя мощность

мгновенная мощность

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

где:

— масса тела

— скорость центра масс тела

— момент инерции тела

— угловая скорость тела.

Физический смысл работы

Работа всех сил, действующих на частицу, идёт на приращение кинетической энергии частицы:

Теорема Кёнига (механика)

Кинетическая энергия системы есть энергия движения центра масс плюс энергия движения относительно центра масс:

,

где T — полная кинетическая энергия,   — энергия движения центра масс,   — относительная кинетическая энергия.

Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы впоступательном движении и энергии системы во вращательном движении относительно центра масс.

В ыразим относительную кинетическую энергию T_r системы S как энергию, вычисленной относительно подвижной системы координат.

Пусть   — радиус-вектор рассматриваемой точки в

подвижной системе координат. Тогда:

Если   — радиус-вектор начала координат подвижной системы, а   — радиус-вектор рассматриваемой точки в исходной системе координат, то верно соотношение:

Вычислим полную кинетическую энергию системы в случае, если начало координат подвижной системы помещено в её центр масс. С учетом предыдущего соотношения:

Раскрывая скобки и вынося из-под знака интеграла, получаем:

П ервое слагаемое представляет собой кинетическую энергию материальной точки, помещённой в начало координат подвижной системы и имеющей массу, равную массе этой системы. Второй член равен нулю, так как по предположению начало координат подвижной системы помещено в её центр масс, следовательно,  

Третий член равен T_r, введённой ранее относительной энергии системы.

Теорема о кинетической энергии для системы частиц.

Теорема об изменении кинетической энергии системы: в дифференциальной форме: dT =  ,

   ,   – элементарные работы, действующих на точку внешних и внутренних сил, в конечной форме:

Т₂ – Т₁=  . Для неизменяемой системы   и   Т₂ – Т₁=  , т.е. изменение кинетической энергии твердого тела на некотором перемещении равно сумме работ внешних сил, действующих на тело на этом перемещении. Если сумма работ реакций связей на любом возможном перемещении системы равна нулю, то такие связи называются идеальными.

Консервативные и неконсервативные силы. Потенциальная энергия частицы во внешнем силовом поле и потенциальная энергия взаимодействия

В современной физике различают четыре вида взаимодействий:

I. гравитационная, или взаимодействие, обусловленное всемирным тяготением;

II. электромагнитная, которая осуществляется через электрические и магнитные поля;

III. сильная или ядерная, которая обеспечивает связь частиц в атомном ядре;

IV. слабая, которая отвечает за численные процессы распада элементарных частиц.

Мы с вами в рамках классической механики будет иметь дело из гравитационными силами и магнитными силами, а также с упругими силами и силами трения. Два последних вида сил определяются характером взаимодействия между молекулами вещества. Силы взаимодействия между молекулами имеют электромагнитное происхождение. Следовательно, упругие силы и силы трения являются по своей природе электромагнитными.

Силы, которые рассматриваются в физике разделяются на консервативные и неконсервативные. Силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным размещением тела в пространстве, называют консервативными, или потенциальными. К ним принадлежат:

- силы притяжения

- силы упругости

- электростатические силы взаимодействия между заряженными телами.

Силы будут консервативными при условии когда в системе нет перехода механического движения в другие формы движения материи, или превращения других форм движения в механический.

Силы, что не принадлежат к консервативным, называют неконсервативными:

- силы трения, которые возникают при скольжении одного тела по поверхности другого

- силы сопротивления, которых испытывает тело, двигаясь в жидкой или газообразной среде.

Эти силы зависят не только от формы тел, но и от их скорости. Они направлены всегда против направления скорости, потому работа сил трения всегда отрицательна.

Гравитационные и электромагнитные силы являются фундаментальными - их нельзя возвести к другим, более простых сил. Упругие силы и силы трения не являются фундаментальными. Законы фундаментальных сил достаточно простые. Убедиться в этом можно из примера.

Вспомним определение силы - это мера внешнего действия на тело, которое возникает в процессе его взаимодействия с другим телом. Это физическая величина введена для характеристики передаваемости движению от одного тела к другому, следовательно, изменения движения взаимодействующих тел. Силу нельзя рассматривать оторвано от материи и ее движения.

Если под действием нескольких сил тело хранит свое состояние спокойствия, или равномерного прямолинейного движения, то такую систему действующих сил будем называть уравновешенной, или эквивалентной нулю.

Результаты действия силы в разных практических примерах более легко объяснить, если различать вслед за Ньютоном статичные и динамические проявления силы. Поэтому различают статичный и динамический способы измерения силы.

Результатами статичного проявления силы является давление на тела, которые препятствуют движению, и их деформация. Понятно, что сила, которая оказывается статично, всегда вызывает равную ей по величине и противоположную за направлением реакцию опоры - силу упругой деформации. Результатом динамического проявления силы являются ускорения - тангенциальное или нормальное. В таком случае силу можно определить по второму закону Ньютона. Но почти везде силы обнаруживают частичного как статичные, так и динамические проявления.

Следовательно, к консервативным силам относят силы притяжения, силы упругости и силы электростатического взаимодействия; к неконсервативным соответственно - силы трения и силы сопротивления.

Момент импульса частицы относительно неподвижного начала и относительно оси. Момент импульса системы частиц.