
- •1. 2. 1 Короткі теоретичні відомості
- •1. 3. 1 Короткі теоретичні відомості
- •2. 1. 1 Короткі теоретичні відомості
- •2. 2. 1 Короткі теоретичні відомості
- •3. 1. 1 Короткі теоретичні відомості
- •3. 2. 1 Короткі теоретичні відомості
- •4.1 Границі числової послідовності та функції
- •4.1.1. Короткі теоретичні відомості
- •4.2.1. Короткі теоретичні відомості
- •4.3.1. Короткі теоретичні відомості
- •5. 1 Поняття функції кількох змінних, її область визначення, границя, неперервність
- •5. 1. 1 Короткі теоретичні відомості
- •5. 2. 1 Короткі теоретичні відомості
- •5. 4. 1. Короткі теоретичні відомості
- •7. 1 Невизначені інтеграли
- •7. 1. 1 Короткі теоретичні відомості
- •7. 2. 1 Короткі теоретичні відомості
- •8. 1 Короткі теоретичні відомості
7. 1 Невизначені інтеграли
7. 1. 1 Короткі теоретичні відомості
1. Поставимо задачу: за заданою функцією F(х) знайти f(х) таку, що f(х) = F'(х). Як відомо, ця дія називається диференціюванням. Обернена задача: за заданою f(х), знайти таку F(х), щоб F'(х) = f(x). Така дія називається інтегруванням. Отже, диференціювання та інтегрування - взаємно обернені дії.
2. Функція F(х) називається первісною функції f(х), якщо х F'(х) = f(х).
Якщо
F(х) -
первісна функції f(х),
то вираз F(х) + С
називається невизначеним
інтегралом від f(х)
і позначається
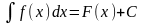 ,
де
,
де
f(х)- підінтегральна функція;
f(х)dx - підінтегральний вираз;
С - довільна стала інтегрування.
3. Властивості невизначеного інтеграла:
1)
 ;
;
2)
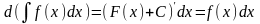 ;
;
3)
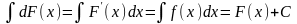 .
.
4. Правила інтегрування:
1)
Сталий множник можна виносити за знак
інтеграла:
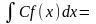
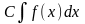
2)
Інтеграл від алгебраїчної суми кількох
функцій дорівнює сумі інтегралів від
цих функцій:
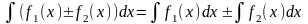
На відміну від правил диференціювання, загальних формул для інтегрування добутку та частки функцій не існує. Інтеграли від добутків та часток розподілені на певні класи та розроблено відповідні методи інтегрування кожного класу.
5. Таблиця інтегралів основних елементарних функцій безпосередньо випливає з таблиці похідних. Справедливість формул перевіряється диференціюванням.
Нехай u = u(x). Тоді
1)
(un)'
= n
un-1
·u'
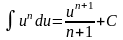 ,
n
-1. При n
=
0
,
n
-1. При n
=
0
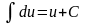 ;
;
2)
(au)'
= au
ln a ·u'
 ;
;
3)
(eu)'
= eu
·u'
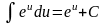 ;
;
4)
(ln
u)' =
·u'
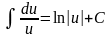 ;
;
5)
(sin
u)'
= cos u ·u'
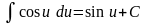 ;
;
6)
(cos
u)' = - sin u ·u'
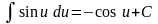 ;
;
7)
(tg
u)' =
·u'
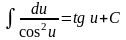 ;
;
8)
(ctg
u)' =
·u'
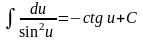 ;
;
9)
(arcsin
u)' =
·u'
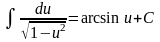 ;
;
10)
(arctg
u)' =
·u'
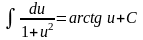 .
.
6. Часто на практиці використовуються інтеграли, які безпосередньо не випливають з таблиці похідних, а знайдені застосуванням певних методів інтегрування:
11)
|
12)
|
13)
|
14)
|
15)
|
16)
|
17)
|
18) |
19)
20)
|
|
Основними методами інтегрування є:
7. Безпосереднє інтегрування. Цей метод полягає в обчисленні інтегралів за допомогою правил інтегрування і таблиці інтегралів. У разі потреби підінтегральну функцію певними алгебраїчними перетвореннями зводять до елементарної табличної функції.
8. Метод заміни змінної (підстановки).
Суть цього методу полягає у введенні нової змінної інтегрування. Він ґрунтується на наступній теоремі:
Теорема 7. 1
Нехай F(х) - первісна функції f(х) на проміжку (а;b), тобто , x(а;b), і нехай функція х = (t) визначена і диференційована на проміжку (;), причому множина значень цієї функції є проміжок (а;b). Тоді справедлива формула:
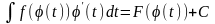 ,
t
(;)
,
t
(;)
Цю теорему застосовують у два способи:
1) Заміна змінної:
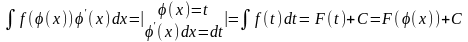 -
-
введення функції під знак диференціала.
2) Підстановка:
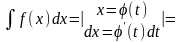 =
=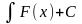 -
-
виведення функції з-під знаку диференціала.
Найпростіша заміна змінної:
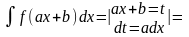
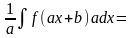
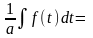
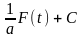 =
=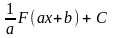
9. Метод інтегрування частинами.
Цей метод застосовується, коли підінтегральна функція є добутком двох функцій, принаймні одна з яких є трансцендентною.
Нехай u = u(х), v = v(х) - деякі диференційовані функції. Тоді справедлива формула
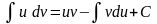 .
.
Застосування:
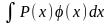 ,
де Р(х)
- многочлен, а
,
де Р(х)
- многочлен, а
1)
(х)
=
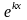 ,
sin kx,
соs kх,
k
R.
,
sin kx,
соs kх,
k
R.
Тоді P(х) = u, (х) dx = dv.
2) (х) = ln x, arcsin x, arccos x, arctg x, arcctg x.
Тоді (х) = u, P(х) dx = dv.
10. Інтегрування раціональних дробів.
Раціональним дробом називається функція вигляду:

Якщо n < m - дріб правильний, якщо n ≥ m, дріб неправильний, тоді його треба представити у вигляді суми цілої частини та правильного дробу:
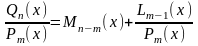 .
.
Далі знаменник дробу розкладається на множники за теоремою 7. 2.
Теорема 7. 2
Всякий многочлен n-го степеня можна подати у вигляді:
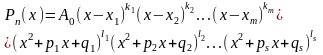
де
х -
змінна, решта - сталі, причому
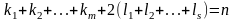 ,
а всі
,
а всі
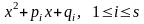 мають D
< 0. Цей вираз називається розкладом
многочлена на множники.
Він має дійсні та комплексні корені,
прості та кратні.
мають D
< 0. Цей вираз називається розкладом
многочлена на множники.
Він має дійсні та комплексні корені,
прості та кратні.
Залежно від множників, на які розкладено раціональний дріб, він може бути представлений у вигляді суми елементарних дробів за теоремою 7. 3.
Елементарними раціональними дробами називаються правильні раціональні дроби чотирьох типів:
1)
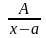 ;
2)
;
2)
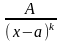 ;
3)
;
3)
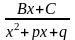 ;
4)
;
4)
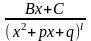 .
.
Теорема 7. 3
Нехай знаменник правильного раціонального дробу розкладено на множники за формулою з теореми 7. 2, тоді цей дріб можна подати у вигляді суми елементарних дробів за формулою:

Невідомі сталі в чисельниках елементарних дробів знаходяться методом порівняння коефіцієнтів.
Інтегрування елементарних дробів:
1)
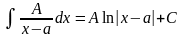 ;
;
2)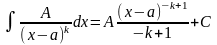 ;
;
3)
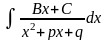 =
=
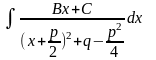 =
=
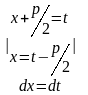 =
=
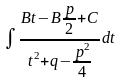 =
=
=
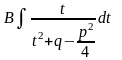 +
+
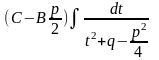 =
=
=
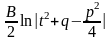 +
+
 =
=
=
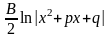 +
+
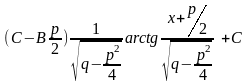 ;
;
4)
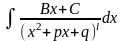 -
розв`язується за допомогою
такої ж підстановки, що і інтеграл
третього типу і повторним інтегруванням
частинами.
-
розв`язується за допомогою
такої ж підстановки, що і інтеграл
третього типу і повторним інтегруванням
частинами.
11. Інтегрування ірраціональних функцій
Ірраціональні функції (ті, що містять змінну у дробових степенях) інтегруються за допомогою підстановок.
1)
 - нехай k
- спільний знаменник дробів
- нехай k
- спільний знаменник дробів
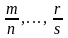 .
Тоді застосовується підстановка:
.
Тоді застосовується підстановка:
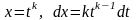 ;
;
2)
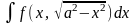 Підстановка: х = а sin
t, або х
= а соs t;
Підстановка: х = а sin
t, або х
= а соs t;
3)
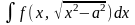 Підстановка: х = а/sin
t, або х
= а/соs t;
Підстановка: х = а/sin
t, або х
= а/соs t;
4)
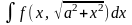 Підстановка: х = а tg t,
або х = а сtg t.
Підстановка: х = а tg t,
або х = а сtg t.
12. Інтегрування тригонометричних функцій.
1)
 .
Застосовується універсальна тригонометрична
підстановка:
.
Застосовується універсальна тригонометрична
підстановка:
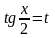 ,
тоді
,
тоді
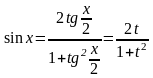 ,
,
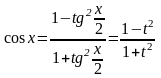 ,
,
x
= 2 arctg
t,
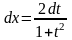 ;
;
2)
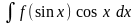 ,
заміна змінної sin x =
t;
,
заміна змінної sin x =
t;
3)
 ,
заміна змінної соs x =
t;
,
заміна змінної соs x =
t;
4)
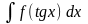 ,
заміна змінної tg
x = t.
,
заміна змінної tg
x = t.
Також для інтегрування тригонометричних функцій використовуються тригонометричні формули зниження степеня:
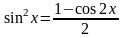 ,
,
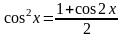 ,
,
та формули розкладення добутку тригонометричних функцій в суму:
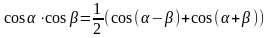 ;
;
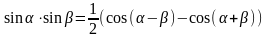 ;
;
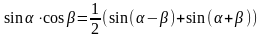 ,
,
Та інші формули перетворення тригонометричних функцій.
Визначені інтеграли

 ;
;
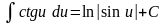 ;
;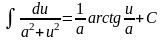 ;
; ;
;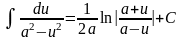 ;
;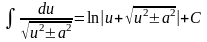 ;
;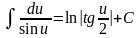 ;
;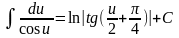 ;
;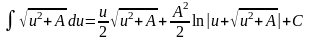 ;
;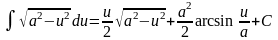 .
.