5. 4. 1. Короткі теоретичні відомості

1. Нехай функція z = z(х, у) визначена в області D, точка М₀(х₀, у₀)  D. Якщо існує окіл точки М₀ з області D, і для всіх відмінних від М₀ точок М цього околу виконується нерівність z(М) < z(М₀) (z(М) > z(М₀)), то М₀ називається точкою локального максимуму (мінімуму) функції z(х, у), а число z(М₀) - локальним максимумом (мінімумом).

2. Необхідна умова екстремуму

Якщо функція z = z(х, у) досягає в точці М₀(х₀, у₀) екстремуму (ехtr), то 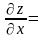0 та 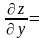0 або не існують в цій точці. Такі точки називаються критичними (стаціонарними) або підозрілими на ехtr.

3. Достатня умова екстремуму

Нехай точка М₀(х₀, у₀) - критична точка функції z = z(х, у) і в цій точці та деякому її околі функція має неперервні частинні похідні 2-го порядку.

Позначимо а₁₁ = 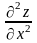, а₂₂ = 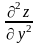, а₁₂ = а₂₁ = .

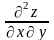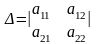, тоді

1) якщо  > 0, то М₀ - ехtr, причому при а₁₁ < 0 - mах, а при а₁₁ > 0 min;

2) якщо  < 0, то т.М₀ - не є ехtr;

3) якщо  = 0, то потрібні додаткові методи дослідження.

4. Нехай z = z(х, у) задана та неперервна в замкненій області G. Для того, щоб знайти найбільше (М) та найменше (m) значення функції в цій області, треба:

дослідити її на екстремум;

відібрати серед екстремальних точок ті, що належать області G;

дослідити функцію на екстремум на межі області G. Для цього рівняння межі у = у (х) слід підставити в z = z(х, у), одержати функцію однієї змінної z = z(х) і дослідити її на екстремум;

обчислити значення функції z = z(х, у) в кутових точках області (якщо вони є);

серед екстремальних точок в середині області, на її межі та кутових точок обрати найбільше та найменше.

5. 4. 2 Приклади розв`язування задач

Дослідити функцію z = z(х, у) на безумовний екстремум:

1.

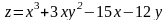
Розв`язування:

Знайдемо критичні точки функції z за необхідною умовою екстремуму:

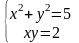
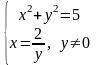
. Після перетворень маємо: 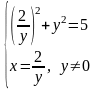  . Перше рівняння після перетворень набуває вигляду: 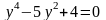, це біквадратне рівняння, розв`язуючи яке знаходимо 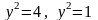. Таким чином, маємо 4 розв`язки: у₁ = 2, у₂ = -2; у₃ = 1; у₄ = -1. Відповідні значення х: х₁ = 1, х₂ = -1; х₃ = 2; х₄ = -2.

Отже, критичними точками є М₁ (1; 2), М₂ (-1; -2), М₃ (2; 1), М₄ (-2; -1). Далі перевіряємо їх на екстремум за достатньою умовою. Для цього знаходимо всі похідні другого порядку функції z. , , 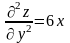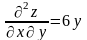. Складаємо визначник: 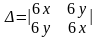= 36 (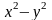 ). Обчислимо значення визначника в кожній критичній точці, підставивши їхні координати:

 (М₁) = 36 (1 – 4) = - 108 < 0, тобто т. М₁ не є екстремальною.

 (М₂) = - 108 < 0, т. М₂ також не є екстремальною.

 (М₃) = 36 (4 – 1) = 108 > 0, тобто т. М₃ – екстремум, причому 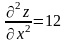> 0, значить М₃ точка мінімуму.

 (М₄) = 108 > 0, значить М₄ також екстремум, причому 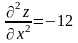< 0, отже М₄ точка максимуму.

Таким чином, серед чотирьох критичних точок екстремальними виявились лише дві. Знайдемо значення функції z в цих точках, підставивши їхні координати в z: z_min (2; 1) = - 28; z_max(-2; -1) = 28.

2.

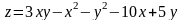
Розв`язування:

Дослідження проводимо за тією ж схемою, що й у попередньому прикладі:

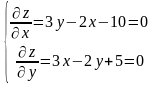
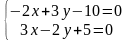 . Домножимо перше рівняння на 3, а друге - на 2 і почленно додамо їх: 5у – 20 = 0  у = 4. Підставивши це значення у в будь-яке з рівнянь системи одержимо відповідне значення х: х = 1. Отже, критична точка одна: М(1; 4). Перевіряємо достатню умову:

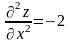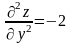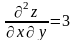, , . Складаємо визначник: = -5 < 0, тобто т. М не є екстремальною.

Відповідь: задана функція екстремумів не має.

ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ