5. 1 Поняття функції кількох змінних, її область визначення, границя, неперервність

5. 1. 1 Короткі теоретичні відомості

1. Змінна величина u, що залежить від n незалежних змінних х₁, х₂, ..., х_n називається функцією n змінних. Окремим випадком є функція двох змінних z = z(х, у).

2. Сукупність усіх числових значень, що набувають змінні х₁, х₂, ..., х_n , при яких функція u набуває певних дійсних значень, називається областю визначення функції u = u(х₁, х₂, ..., х_n) і позначається D (рис. 5.1).

3. Околом радіуса r т. М₀(х₀, у₀) називається сукупність усіх точок М(х,у), що задовольняють нерівності 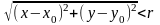(рис. 5.2)

4. Число А називається границею функції z = z(х, у) при М(х,у)  М₀(х₀, у₀), якщо  > 0 знайдеться таке r > 0, що для будь-якої М(х, у) з r - околу точки М₀(х₀, у₀) виконується нерівність . Позначається

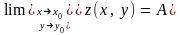
5. Нехай точка М₀(х₀, у₀)  D(z(х,у)). Функція z = z(х,у) називається неперервною в точці М₀(х₀, у₀), якщо , незалежно від способу прямування М(х,у)  М₀(х₀, у₀).

6. Функція, неперервна в будь-якій точці деякої області, називається неперервною в цій області.

7. Властивості неперервних функцій в замкненій області:

1) області визначення D та неперервності збігаються;

2) неперервна функція обмежена

2 Частинні похідні функції кількох змінних. Повний диференціал

5. 2. 1 Короткі теоретичні відомості

1. Розглянемо функцію двох змінних z = z(х, у). Нехай її аргументи х₀ та у₀ набули приросту х та у: х = х₀ + х , у = у₀ + у Отже, приріст аргументів функції z = z(х, у): х = х - х₀, у = у – у₀.

Тоді повним приростом функції буде:

z = z(х,у) - z(х₀,у₀) = z( x₀+х , y₀+у ) - z(x₀,y₀).

Якщо надати приросту тільки одній змінній, а другу залишити сталою, то функція набуде частинних приростів:

_x z = z( x₀+х , y₀) - z(x₀,y₀) - частинний приріст функції по змінній х;

_у z = z( x₀, y₀+у ) - z(x₀,y₀) - частинний приріст функції по змінній у.

2. Якщо існує , то вона називається частинною похідною функції z = z(х,у) по змінній х. Позначається : 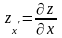. Аналогічно = .

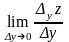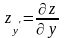Обчислюються частинні похідні по змінній х_і за допомогою правил диференціювання та таблиці похідних, вважаючи х_і змінною, а решту змінних - сталими величинами.

3. Нехай z = z(х, у) визначена в деякому околі точки М(х, у), тоді функція z = z(х, у) називається диференційованою в точці М, якщо її повний приріст z можна подати у вигляді: z = А х + В у +  х +  у,

де А, В - дійсні числа, що не залежать від х, у;

,  - нескінченно малі, тобто ,   0 при х, у  0.

Знайдемо сталі А, В. Для цього розглянемо окремий випадок, коли у = 0. Повний приріст z стає частинним _х z  _х z = А х +  х, цей вираз розділимо на х та знайдемо границю при х  0 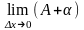 = = А,  А = . Аналогічно В = .

4. Повним диференціалом функції z = z(х, у) називається головна лінійна частина повного приросту функції: dz = А х + В у; х dx; у dy 

dz = dх + dу.

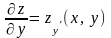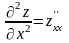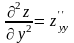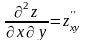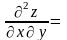
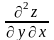5. Частинні похідні першого порядку та є також функціями змінних х та у. Їх можна знову продиференціювати по кожній змінній: , , причому для мішаної похідної виконується властивість: , тобто значення мішаної похідної не залежить від порядку диференціювання.

6. Частинною похідною n-го порядку називається перша похідна від похідної (n-1) порядку.

Безумовний екстремум функції кількох змінних.

Найбільше та найменше значення функції у замкненій області