
- •1. 2. 1 Короткі теоретичні відомості
- •1. 3. 1 Короткі теоретичні відомості
- •2. 1. 1 Короткі теоретичні відомості
- •2. 2. 1 Короткі теоретичні відомості
- •3. 1. 1 Короткі теоретичні відомості
- •3. 2. 1 Короткі теоретичні відомості
- •4.1 Границі числової послідовності та функції
- •4.1.1. Короткі теоретичні відомості
- •4.2.1. Короткі теоретичні відомості
- •4.3.1. Короткі теоретичні відомості
- •5. 1 Поняття функції кількох змінних, її область визначення, границя, неперервність
- •5. 1. 1 Короткі теоретичні відомості
- •5. 2. 1 Короткі теоретичні відомості
- •5. 4. 1. Короткі теоретичні відомості
- •7. 1 Невизначені інтеграли
- •7. 1. 1 Короткі теоретичні відомості
- •7. 2. 1 Короткі теоретичні відомості
- •8. 1 Короткі теоретичні відомості
4.2.1. Короткі теоретичні відомості
1.
Функція у
= f
(x),
визначена в точці х0
і деякому околі цієї точки, називається
неперервною
в точці хо,
якщо
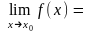
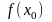 .
.
Іншими словами, якщо х х0 , тобто (х - х0) 0, то , тобто
(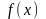 -
)
0
-
)
0
х - х0 = x - називається приростом аргументу;
f(x) - f(x0) = f(x0 + x) - f(x0) = у - приріст функції, отже означення неперервної функції можна дати по-іншому:
Функція у = f (x), визначена в точці х0 і деякому околі цієї точки, називається неперервною в точці х0, якщо х та у в цій точці є нескінченно малими величинами (тобто нескінченно малому приросту аргумента відповідає нескінченно малий приріст функції).
2. Якщо функція неперервна в точці деякого інтервала, то вона називається неперервною в інтервалі.
3. Умови неперервності:
Функція
у
= f
(x)
буде
неперервною в точці х0
тоді і тільки тоді,
коли
вона визначена в деякому
околі точки х0
і виконується:
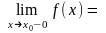
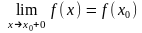
Якщо хоча б одна рівність не виконується, то х0 - точка розриву.
1)
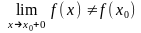 -
розрив
1 роду
усувний
або ліквідовний.
-
розрив
1 роду
усувний
або ліквідовний.
2)
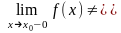
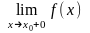 ,
обидві границі скінченні -
розрив
1 роду,
стрибок;
,
обидві границі скінченні -
розрив
1 роду,
стрибок;
величина
стрибка
= |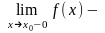 |
|
3) , причому хоча б одна з границь не існує або нескінченна, - розрив 2 роду.
Надалі будемо використовувати такі умовні позначення:
- 0 – від`ємна нескінченно мала;
+ 0 – додатна нескінченно мала;
- - від`ємна нескінченно велика;
+ - додатна нескінченно велика;
а – 0 – число, що менше за а на нескінченно малу;
а + 0 – число, що більше за а на нескінченно малу.
Диференціальне числення функції однієї змінної
4.3.1. Короткі теоретичні відомості
Однією з основних характеристик функції є її похідна в певній точці. Найбільш наочне уявлення про зміст похідної дає її геометрична інтерпретація. Тому розглянемо задачу про дотичну до кривої.
1. Дотичною до кривої у = f(x) в точці М(х; у) називається граничне положення січної ММ1, коли точка М1, рухаючись по кривій, прямує до точки дотику М.
Знайдемо кутовий коефіцієнт дотичної (рис. 4.18): надамо аргументу х приросту х, відповідний йому приріст функції у буде у, тоді координати точки М1 (х + х; у +у).
З
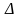 MM1A:
MM1A:
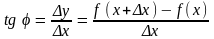 .
.
Якщо
х
 0, точка М1
М,
січна повертається навколо точки М
і намагається зайняти положення дотичної,
а кут
0, точка М1
М,
січна повертається навколо точки М
і намагається зайняти положення дотичної,
а кут

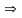
 .
Тангенс кута нахилу дотичної до кривої
в точці М
і є похідною функції у цій точці.
.
Тангенс кута нахилу дотичної до кривої
в точці М
і є похідною функції у цій точці.
2. Похідною функції у = f(x) по аргументу х називають границю відношення приросту функції до прироста аргумента, коли приріст аргумента прямує до нуля:
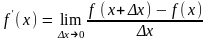 .
.
Похідна
функції може позначатись у такий спосіб:
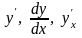 .
.
Операцію знаходження похідної називають диференціюванням, а функцію, що має похідну в деякій точці, називають диференційовною в цій точці.
3. Теорема (зв'язок між неперервністю та диференційовністю)
Якщо функція у = f (x) диференційовнана в деякій точці х0, то вона в цій точці неперервна.
Обернене твердження не справедливо: не кожна неперервна в точці функція буде диференційовною в цій точці.
4. Правила диференціювання:
Якщо С – стала, то С' = 0.
Якщо
функції u
= u(x)
та v
= v(x)
диференційовні
в точці х,
то їхня алгебраїчна
сума, добуток та частка (v(x)
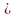 0
) теж
диференційовні
в цій точці і справедливі формули:
0
) теж
диференційовні
в цій точці і справедливі формули:
2.1. (u ± v)' = u' ± v';
2.2. (uv)' = u'v + v'u;
2.3.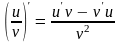 .
.
Сталий множник можна виносити за знак похідної: (Cu)' = Cu'.
Диференціювання складеної функції: якщо y = f(u), u = u(x) і функції f та u
диференційовні по своїх аргументах, то yx' = fu' ux'.
Диференціювання
обернених функцій: нехай функція у
= у(х)
має обернену х
= х(у),
причому обидві функції диференційовні,
тоді
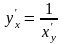 .
.
5. Таблиця похідних основних елементарних функцій.
Нехай u = u(x). Тоді
1. (un)' = n un-1 ·u' |
8.
(tg
u)' =
|
2. (au)' = au ln a ·u' |
9.
(ctg
u)' =
|
3. (eu)' = eu ·u' |
10.
(arcsin
u)' =
|
4.
(logau)'
=
|
11. (arccos u)' = - ·u' |
5. (ln u)' = ·u' |
12.
(arctg
u)' =
|
6. (sin u)' = cos u ·u' |
13. (arcctg u)' = - ·u' |
7. (cos u)' = - sin u ·u' |
|
6. Диференціювання функцій, що задані неявно та параметрично.
Неявно задана функція має вигляд F(х; у) = 0. Щоб продиференціювати її, треба взяти похідну по х від обох частин рівності, враховуючи, що у = у(х), і одержане рівняння розв'язати відносно у', у' = у'(х; у).
Параметрично
задана
функція має вигляд
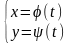 ,
t
,
t
- параметр.
,
t
,
t
- параметр.
Її
похідна обчислюється за формулою:
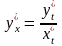 .
.
7. Похідні вищих порядків
Нехай на інтервалі (а; b) задана диференційовна функція у = f (х), тоді її похідна f (х) (похідна першого порядку) також є функцією від х. Якщо ця функція диференційовна на (а; b), то її похідна називається похідною другого порядку у і т.д. Похідною n – го порядку функції у називається похідна 1 – го порядку від похідної (n – 1)-го порядку: у(n) = (у(n-1))' .
8. Правило Лопіталя
Правило,
що дає змогу розкривати невизначеності
вигляду
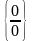 та
та
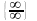 за
допомогою похідних, сформульовано у
наступній теоремі.
за
допомогою похідних, сформульовано у
наступній теоремі.
Теорема.
Нехай функції f(x)
та g(x)
визначені та диференційовні в околі
точки х0
і
в цьому околі
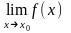 =
=
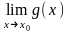 =
0 або
=
=
,
причому
g'(x)
0. Тоді якщо
=
0 або
=
=
,
причому
g'(x)
0. Тоді якщо
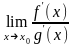 ,
то
,
то
 ,
і
ці границі рівні
між собою.
,
і
ці границі рівні
між собою.
9. Диференціал та його геометричний зміст
Диференціалом dy функції у = f (х) в точці х називається головна, лінійна відносно х, частина приросту функції f (х) в цій точці: dy = f (х) dx.
10. Основні теореми диференціального числення
Теорема Лагранжа
Якщо функція у = f(x), неперервна на відрізку [а; b], диференційовна в інтервалі (а; b), то в середині цього інтервалу знайдеться хоча б одна точка с (а; b), в який f(b) – f(a) = f `(c) (b-a)
Теорема Ролля
Якщо функція у = f(x), неперервна на відрізку [а; b], диференційовна в інтервалі (а; b) і на кінцях відрізка набуває однакових значень f(a) = f(b), то знайдеться хоча б одна точка с (а; b), в який f `(c) = 0
11. Функція у = f(x) називається монотонно зростаючою на (а; b), якщо х1 < х2 з інтервалу (a; b) f(x1) < f(x2)
Функція у = f(x) називається монотонно спадною на (а; b), якщо х1 < х2 з інтервалу (a; b) f(x1) > f(x2)
Рис. 4. 11
12. Теорема (необхідна ознака зростання (спадання) функції)
Якщо диференційовна на (а; b) функція зростає (спадає), то f (х) 0 ( f (х) 0 )
Теорема (достатня ознака зростання (спадання) функції)
Якщо у = f(x) диференційовна на (а; b) функція і f (х) > 0 (f (х) < 0 ) на (а; b), то функція зростає (спадає) на цьому проміжку.
13. Інтервали монотонності функції відділяються один від одного точками, у яких похідна = 0, або не існує. Такі точки називаються критичними точками 1 роду.
14. Функція у = f(x) має екстремум в точці х0, якщо такий окіл точки х0, для всіх х якого виконується нерівність: f(x) < f(x0) – для максимума і f(x) > f(x0) - для мінімума (рис. 4. 12).
15. Теорема (достатня умова екстремуму функції)
Нехай функція у = f(x) диференційовна в околі точки x0, крім можливо самої точки x0, яка є критичною точкою 1 роду. Тоді якщо
1) f ´(х) > 0 х < х0 і f ´ (х) < 0 х > х0, то х0 є точкою максимума;
2) f ´(х) < 0 х < х0 і f ´ (х) > 0 х > х0, то х0 є точкою мінімума;
3) якщо при переході через точку х0 похідна не змінює знак, то х0 не є екстремальною.
16. Крива у = f(x) називається опуклою на (а; b), якщо всі її точки лежать нижче довільної дотичної на цьому інтервалі.
Крива у = f(x) називається вгнутою на (а; b), якщо всі її точки лежать вище довільної дотичної на цьому інтервалі.
Точкою перегину називається така точка кривої, яка відділяє її опуклу частину від вгнутої. Отже, в точці перегину дотична перетинає криву (рис. 4. 13).
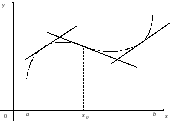
Рис. 4. 13
Теорема
Нехай функція у = f (x) двічі диференційовна на (а; b), тоді якщо
1) f `` (х) > 0 х (а; b), то крива вгнута на цьому інтервалі;
2) f `` (х) < 0 х (а; b), то крива опукла на (а; b).
Інтервали опуклості і вгнутості відділяються один від одного точками, де похідна другого порядку дорівнює 0, або не існує (критичними точками 2 роду).
17. Теорема (достатня умова існування точки перегину)
Нехай функція у = f (x) двічі диференційовна в околі точки х0, крім можливо самої точки х0, яка є критичною точкою 2 роду. Тоді якщо при переході через х0 похідна другого порядку змінює знак, то х0 є точкою перегину кривої у = f (x).
Пряма l називається асимптотою кривої, якщо відстань від змінної точки М кривої до l прямує до нуля, коли точка М, рухаючись по кривій, віддаляється на нескінченність (рис. 4. 14).
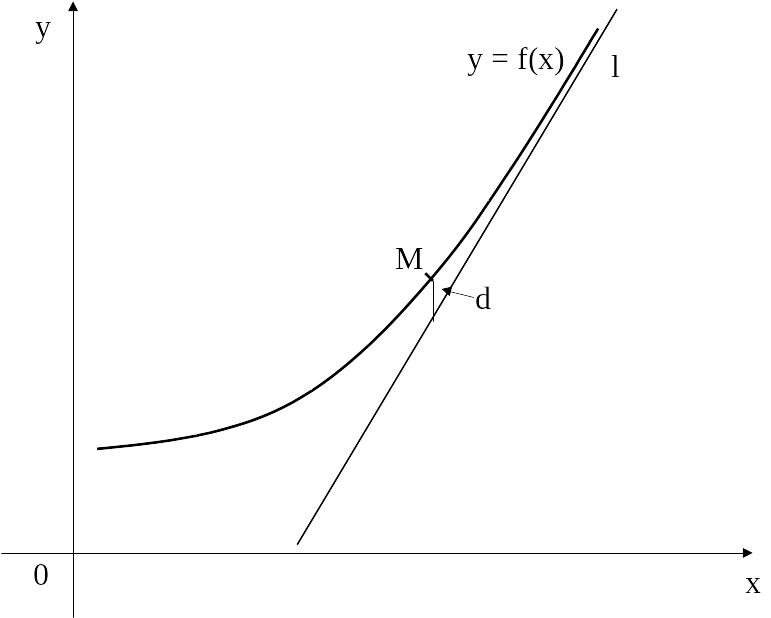
Рис. 4. 14
19. Асимптоти бувають вертикальними, горизонтальними та похилими.
Умова
існування вертикальної асимптоти х
= а
:
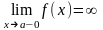 ,
або
,
або
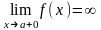 ,
або
,
або
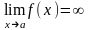 ,
тобто
функція має розрив
2 роду.
,
тобто
функція має розрив
2 роду.
Рівняння похилої асимптоти знаходять у вигляді у = kx + b, де
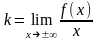 ,
а
,
а
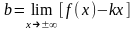 .
.
Якщо k = 0, то похила асимптота буде горизонтальною. Якщо принаймні одна з границь, що визначають k і b, не існує або дорівнює нескінченості, то похилої асимптоти немає.
20. При проведенні повного дослідження функції та побудові її графіка користуються наступним алгоритмом:
1. знаходять область визначення функції;
2. визначають точки перетину графіка з осями координат;
3. досліджують на парність та періодичність;
4. визначають точки та характер розриву функції;
5. знаходять інтервали монотонності та екстремуми;
6. визначають інтервали опуклості-вгнутості та точки перегину;
7. знаходять рівняння асимптот;
8. за даними дослідження будують графік функції.
ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ КІЛЬКОХ ЗМІННИХ

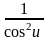 ·u'
·u'
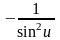 ·u'
·u'
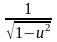 ·u'
·u'
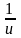 logae
·u'
=
logae
·u'
=
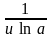 ·u'
·u'
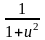 ·u'
·u'