
- •1. 2. 1 Короткі теоретичні відомості
- •1. 3. 1 Короткі теоретичні відомості
- •2. 1. 1 Короткі теоретичні відомості
- •2. 2. 1 Короткі теоретичні відомості
- •3. 1. 1 Короткі теоретичні відомості
- •3. 2. 1 Короткі теоретичні відомості
- •4.1 Границі числової послідовності та функції
- •4.1.1. Короткі теоретичні відомості
- •4.2.1. Короткі теоретичні відомості
- •4.3.1. Короткі теоретичні відомості
- •5. 1 Поняття функції кількох змінних, її область визначення, границя, неперервність
- •5. 1. 1 Короткі теоретичні відомості
- •5. 2. 1 Короткі теоретичні відомості
- •5. 4. 1. Короткі теоретичні відомості
- •7. 1 Невизначені інтеграли
- •7. 1. 1 Короткі теоретичні відомості
- •7. 2. 1 Короткі теоретичні відомості
- •8. 1 Короткі теоретичні відомості
4.1.1. Короткі теоретичні відомості
Умовні позначення: - для всіх, кожний, будь-який; - існує.
1. Величиною називається все те, що можна охарактеризувати числовим значенням та виразити в певних одиницях виміру.
2. Величина, числове значення якої при умовах, що розглядаються, не змінюється, називається сталою, набуває різних значень - змінною.
3. Змінна величина х називається нескінченно малою величиною, якщо в процесі її зміни наступить такий момент, починаючи з якого х стає і залишається менше будь-якого, скільки завгодно малого, наперед заданого числа 0 : х| .
Позначення: х 0 або lim х = 0
4. Змінна величина х називається нескінченно великою величиною, якщо в процесі її зміни наступить такий момент, починаючи з якого х| стає і залишається більше будь-якого, скільки завгодно великого, наперед заданого числа М > 0 : |х| > М.
Позначення: х або lim х =
5. Зв'язок між нескінченно малими та нескінченно великими обернений: нехай - нескінченно мала, а - нескінченно велика, тоді = 1/ .
6. Властивості нескінченно малих та нескінченно великих величин:
1) Алгебраїчна сума скінченного числа нескінченно малих є величина нескінченно мала.
2) Добуток обмеженої величини на нескінченно малу є величина нескінченно мала.
Наслідки:
1) Добуток нескінченно малої на сталу величину є величина нескінченно мала.
2) Добуток скінченої кількості нескінченно малих є величина нескінченно мала.
Аналогічні властивості для нескінченно великих, за винятком різниці нескінченно великих.
7. Якщо nN за певним правилом ставиться у відповідність число хn , то множину {х1, х2, ... , хn , ...} називають числовою послідовністю і позначають {хn, n 1}.
8. Стала величина а називається границею числової послідовності {хn, n 1}, якщо 0, наперед заданого, як завгодно малого такий номер N = N(), що n > N виконується нерівність: |хn- а| .
Це означає, що інтервал (а - ; а + ) містить всі члени числової послідовності, починаючи з деякого номера. Чим менше ми оберем , тим пізніше почне виконуватись зазначена властивість (рис. 4. 1).

рис. 4. 1
Позначення:
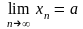 .
.
9. Послідовність, що має скінченну границю, називається збіжною, в інших випадках - розбіжною.
10. Якщо х X за певним правилом поставлене у відповідність певне дійсне число у У ,то кажуть, що у є функцією від х : y = f (x)
11. Нехай функція y = f (x) визначена в деякому околі точки х0 (крім можливо самої точки х0). Число А називається границею функції в точці х0, якщо 0, наперед заданого, як завгодно малого число = () > 0 таке, що х : |х - x0| < виконується нерівність: |f(x) - A| < .
Це означає, що для всіх значень х, які достатньо мало відрізняються від числа x0, відповідні значення функції f(x) як завгодно мало відрізняються від числа A.
Позначення:
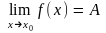
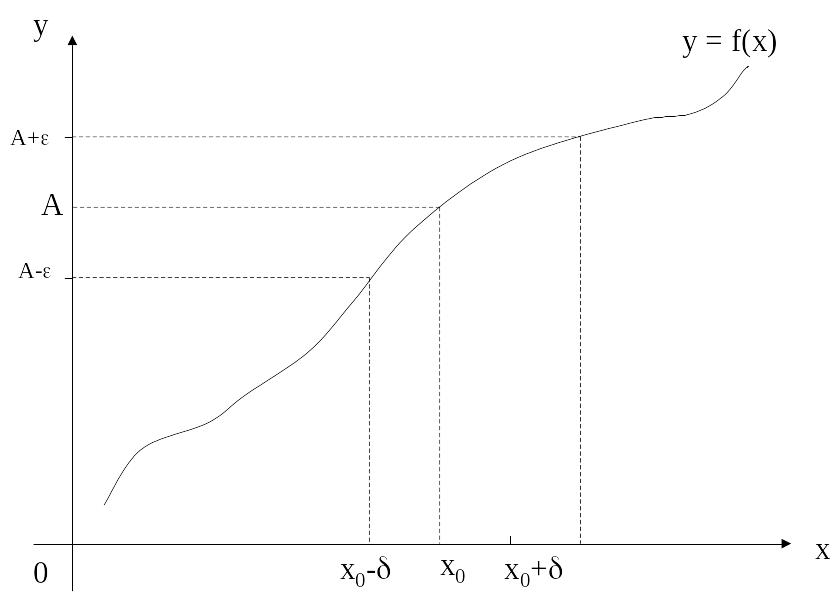
рис. 4.3
12. При х число А називається границею функції на нескінченності, якщо для всіх достатньо великих значень х відповідні значення функції f(x) як завгодно мало відрізняються від числа А.
13. У наведених означеннях границь вважалось, що х х0 довільним способом, але можливі випадки, коли х х0, залишаючись зліва від х0 (тобто х < х0), або справа від х0 (тобто х > х0). Такі границі називають односторонніми і позначають:
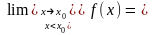
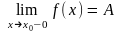 -
лівостороння границя;
-
лівостороння границя;

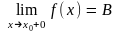 -
правостороння границя.
-
правостороння границя.
14. Теорема. Якщо кожна з функцій f(x) та g(x) має скінченну границю в точці х0, то в цій точці також границі функцій f(x) ± g(x); f(x)g(x) та f(x) / g(x) (якщо границя g(x) 0) і справедливі формули:
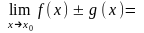
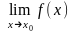
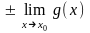 ;
;
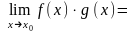
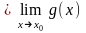 ;
;
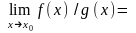 .
.
Наслідки:
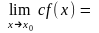 с
;
с
;
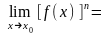 [
]
[
]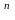
15.
Функції
1(х)
та 2(х),
нескінченно малі
при х
х0,
називаються еквівалентними,
якщо
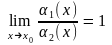 .
Позначення:
1(х)
~
2(х)
.
Позначення:
1(х)
~
2(х)
16.
Теорема Нехай 1(х)
~
1´(х),
2(х)
~
2´(х),
при х
х0.
Якщо  ,
то
,
то 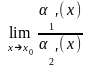 і
ці границі рівні між собою.
і
ці границі рівні між собою.
17. Еквівалентними нескінченно малими при х 0 є наступні функції:
sin х ~ х, |
arctg х ~ х, |
|
arcsin х ~ х, |
1-
cos
х ~
|
ln (1 + х) ~ х, |
tg х ~ х , |
|
|
18. Чудові границі:
1
чудова
границя:
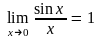
2
чудова границя:
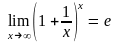 ,
де е –
ірраціональне число, яке наближено
дорівнює 2.71828…
,
де е –
ірраціональне число, яке наближено
дорівнює 2.71828…
Друга
чудова границя може мати інший вигляд:
зробимо заміну 1/х =
у, тоді
при х
, у
0 і
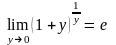
19.
У
найпростіших випадках знаходження
границі
зводиться
до підстановки в f
(x) граничного
значення аргументу х0.
Але пряма підстановка не завжди призводить
до відповіді. Іноді однакові дії з
нескінченно
малими
та нескінченно
великими
функціями дають різні результати.
Наприклад, нехай
- нескінченно
мала, a
= 2,
= 2
- теж
нескінченно
малі, тоді
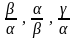 - будуть
відповідно нескінченно
малою, нескінченно
великою
та
сталою величинами.
Аналогічно для нескінченно
великих.
Така ситуація при знаходженні границь
називається невизначеністю.
- будуть
відповідно нескінченно
малою, нескінченно
великою
та
сталою величинами.
Аналогічно для нескінченно
великих.
Така ситуація при знаходженні границь
називається невизначеністю.
20.
Основними типами невизначеностей є
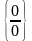 ,
,
 ,
,
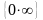 ,
,
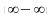 ,
,
 ,
,
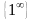 ,
,
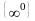 .
.
В разі, якщо підстановка граничного значення аргументу призводить до невизначеності, слід таким чином перетворити функцію f (x) , щоб позбутись цієї невизначеності. Таке перетворення функції називається розкриттям невизначеності. Методи розкриття невизначеностей залежать від типу функції f (x) та типу невизначеності.
Неперервність функцій

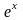 -
1 ~
х,
-
1 ~
х,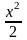 ,
, -
1 ~
lna
-
1 ~
lna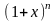 ~
nх
~
nх