3. 1. 1 Короткі теоретичні відомості

1. Рівняння прямої, що проходить через задану точку М₀(х₀; у₀) перпендикулярно до заданого вектора 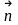= (А; В) ( - нормаль): А(х – х₀) + В(у – у₀) = 0.

2. Рівняння прямої, що проходить через задану точку М₀(х₀; у₀) паралельно заданому вектору 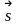= (l; m) (канонічне рівняння, - напрямний вектор):

.

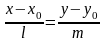3. Параметричне рівняння прямої: 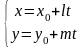, t – параметр.

4. Загальне рівняння прямої: Ах + Ву + С = 0.

5. Рівняння прямої, що проходить через дві задані точки М₁(х₁; у₁) та М₂(х₂; у₂):

.

6. Рівняння прямої у відрізках на осях (пряма відтинає від координатних осей ОХ та ОУ відрізки а і b відповідно): .

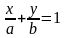7. Рівняння прямої з кутовим коефіцієнтом (пряма проходить через задану точку М₀(х₀; у₀) під кутом  до додатнього напрямку осі ОХ: у – у₀ = tg (х – х₀), або

у = kx + b (k = tg).

8. Ознаки паралельності та перпендикулярності прямих, знаходження кута між прямими.

1) Дві прямі, задані загальними рівняннями паралельні (перпендикулярні), якщо паралельні (перпендикулярні) їхні нормалі. Нехай дві прямі задані загальними рівняннями: А₁х + В₁у + С₁ = 0, 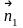= (А₁; В₁),

А₂х + В₂у + С₂ = 0, 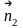= (А₂; В₂).

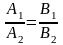- умова паралельності прямих,

А₁А₂ + В₁В₂ = 0 – умова перпендикулярності прямих.

Кут між прямими дорівнює куту між нормалями:

= .

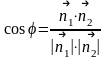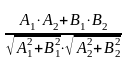2) Дві прямі, задані канонічними рівняннями паралельні (перпендикулярні), якщо паралельні (перпендикулярні) їхні напрямні вектори. Нехай дві прямі задані канонічними рівняннями: 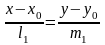, = (l₁; m₁) ,

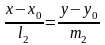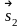, = (l₂; m₂).

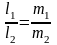- умова паралельності прямих,

l₁l₂ + m₁m₂ = 0 – умова перпендикулярності прямих.

Кут між прямими дорівнює куту між напрямними векторами:

= .

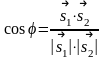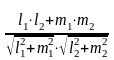3) Дві прямі, задані рівняннями з кутовим коефіцієнтом: у = k₁x + b₁, у = k₂x + b₂ паралельні, якщо k₁ = k₂ і перпендикулярні, якщо k₁  k₂ = -1.

Кут між прямими: .

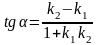9. Відстань від точки М₀(х₀; у₀) до прямої Ах + Ву + С = 0 обчислюється за формулою: .

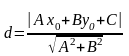Пряма та площина в просторі

3. 2. 1 Короткі теоретичні відомості

1. Рівняння площини, що проходить через задану точку М₀(х₀; у₀; z₀) перпендикулярно до заданого вектора = (А; В; C):

А(х – х₀) + В(у – у₀) + C(z – z₀) = 0.

2. Загальне рівняння площини в просторі: Ах + Ву + Cz + D = 0.

3. Рівняння площини, що проходить через три точки М₁(х₁; у₁; z₁), М₂(х₂; у₂; z₂) та М₃(х₃; у₃; z₃) знаходять за формулою: .

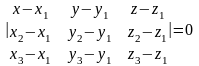4. Рівняння площини у відрізках на осях: 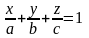, де а, b, c – відрізки, що відтинає площина від координатних осей ОХ, ОУ, ОZ відповідно.

5. Канонічне рівняння прямої у просторі – це рівняння прямої, що проходить через задану точку М₀(х₀; у₀; z₀) паралельно заданому вектору = (l; m; р) :

.

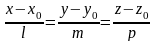6. Параметричне рівняння прямої: 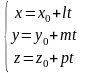, де t – параметр.

7. Рівняння прямої у просторі, що проходить через дві задані точки М₁(х₁; у₁; z₁) та М₂(х₂; у₂; z₂): .

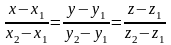8. Відстань від точки М₀(х₀; у₀; z₀) до площини Ах + Ву + Сz + D = 0 обчислюється за формулою: .

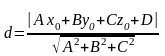4.1 Границі числової послідовності та функції