2. 1. 1 Короткі теоретичні відомості

1. Вектори – це величини, що мають числове значення і напрям, тому геометрично - це напрямлені відрізки.

2. Одиничним називається вектор, довжина якого дорівнює 1.

3. Одиничний вектор, напрям якого збігається з напрямом вектора , називається ортом .

4. Нульовим називається вектор, почток якого збігається з кінцем: 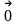. Довжина нульового вектора дорівнює 0, напрям невизначений.

5. Вектори і 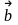називаються колінеарними, якщо вони лежать на одній або паралельних прямих.

6. Вектори і називаються компланарними, якщо вони лежать на одній або паралельних площинах.

7. Проекцією вектора на вісь l називається довжина вектора 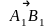взята із знаком "+", якщо напрям вектора і осі однакові, і з знаком "-", якщо вони протилежні (рис. 2. 1). Позначається: .

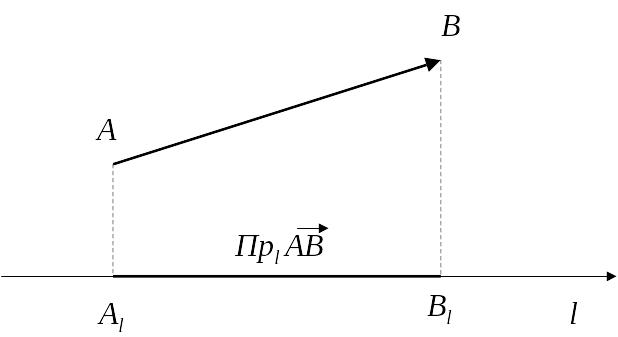
рис. 2. 1

8. Кутом між векторами називається менший з кутів, що утворюють вектори, за умови, що вони зведені до спільного початку: .

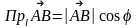9. Розглянемо вектор у ПДСК (OXУZ). Позначимо та знайдемо його проекції на вісі.

Координатами вектора називаються його проекції на осі координат:

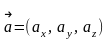, де , , аналогічно для просторового випадку .

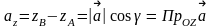10. Косинуси кутів, що утвоює вектор з відповідними осями координат (cos , cos , cos ) називаються напрямними косинусами цього вектора.

11. Довжина вектора знаходиться за формулою: .

12. Дії з векторами: Додавання та віднімання векторів в координатній формі: , , .

Множення вектора на число в координатній формі: .

Скалярний добуток векторів:  = | | | | cos  - в результаті одержуємо число. Геометричний зміст скалярного добутку: = | | , = | | .

Скалярний добуток в координатній формі: = , ,  = a_xb_x+ a_yb_y + a_zb_z.

13. Умова перпендикулярності векторів: кут між векторами  = /2, тому cos  = 0 і  = 0, або в координатній формі a_xb_x+ a_yb_y + a_zb_z = 0.

14. Умовою паралельності векторів є пропорційність їхніх координат: = k ;

k = .

15. Скалярний квадрат вектора дорівнює квадрату його довжини:

( ) =| || |cos0 = | | .

16. Відношенням, у якому точка М поділяє відрізок М₁М₂, називається число , що задовольняє рівності 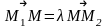. Зв`язок між координатами точок М(х, у, z), М₁(х₁, у₁, z₁), М₂(х₂, у₂, z₂) та  задається рівностями: 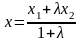; ; . В окремому випадку при діленні відрізка М₁М₂ навпіл ( = 1), формули набувають вигляду: ; ; .

2. 2. 1 Короткі теоретичні відомості

1. Упорядкована множина n дійсних чисел , ,…, називається n – вимірним вектором і позначається = ( , ,…, ).

2. Множина всіх n – вимірних векторів називається n - вимірним простором і позначається Е_n.

3. Лінійною комбінацією векторів , ,…, в Е_n називається вираз 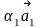+ +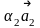…+ 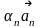, де , ,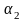…, деякі дійсні числа.

4. Вектори , ,…, називаються лінійно незалежними, якщо їхня лінійна комбінація + +…+ = 0 тоді і тільки тоді, коли всі , ,…, = 0 і лінійно залежними, коли хоча б одне з чисел , ,…,  0.

5. Кожний вектор можна записати як матрицю - стовпець, 0 - як нульовий вектор, тоді векторну рівність + +…+ = 0 можна записати у матричній формі: + +…+ 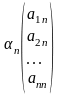= 0 , або 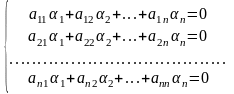- це однорідна СЛАР відносно невідомих , ,…, . Однорідна СЛАР завжди має нульовий розв`язок. Якщо цей розв`язок єдиний, то вектори лінійно незалежні. Показником того, що розв`язок єдиний, є відмінність від нуля основного визначника системи:   0. Якщо нульовий розв`язок не єдиний (існують ще ненульові розв`язки), то вектори лінійно залежні. Показником цього є рівність нулю як основного, так і всіх допоміжних визначників системи:  = 0 та _і = 0 ( і = 1,…, n).

6. Базисом n-вимірного простору називають будь-яку сукупність n лінійно незалежних векторів цього простору.

Якщо в n-вимірному просторі до n базисних векторів додати ще один (n + 1)-ий вектор, то така система стане лінійно залежною і один з цих векторів можна представити лінійною комбінацією інших : 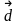= + +…+ , а числа , ,…, називаються координатами в базисі , ,…, . Для того, щоб знайти координати в цьому базисі, треба розв'язати неоднорідну СЛАР:

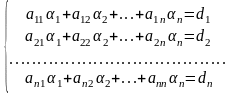
7. На площині два будь-яких неколінеарних вектори утворюють базис і довільний третій вектор може бути представлений лінійною комбінацією базисних (рис. 2. 3).

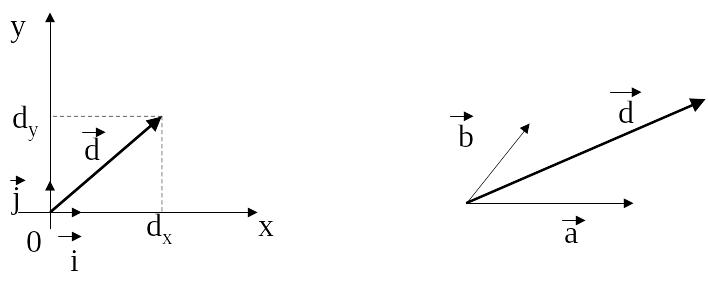
рис. 2. 3

У тривимірному просторі три будь-яких некомпланарних вектори утворюють базис і довільний четвертий вектор може бути представленим лінійною комбінацією базисних. Найчастіше у тривимірному просторі використовують ортонормований координатний базис, це трійка векторів 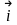=(1; 0; 0), = (0; 1; 0), = (0; 0; 1), їхній напрям збігається з напрямом відповідниї координатних осей, а довжина дорівнює одиниці. Будь-який вектор може бути розкладений за базисом , , , тобто представлений у вигляді: = + + 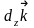, де числа 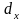, , - координати вектора в цьому базисі: = ( , , ). Обираючи у якості базиса іншу трійку некомпланарних векторів: , , та розкладаючи вектор в цьому базисі, одержимо інші його координати: = + + ,

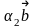= ( , , ) (рис. 2. 4).

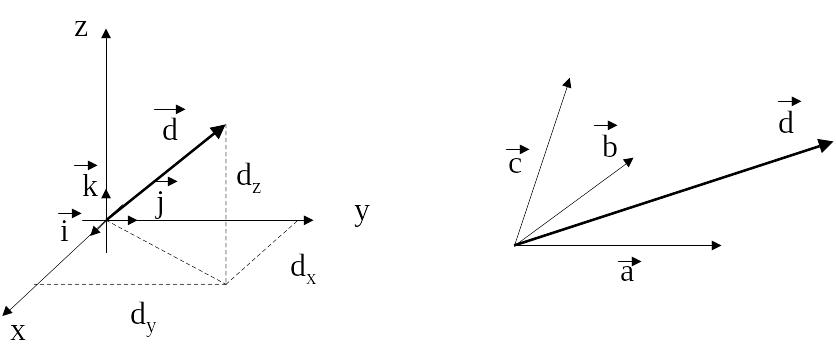
рис. 2. 4

АНАЛІТИЧНА ГЕОМЕТРІЯ

3. 1 Пряма на площині