8. 1 Короткі теоретичні відомості

При досліжденні різноманітних процесів та явищ, що містять елементи руху, користуються математичними моделями у вигляді рівнянь, до яких, крім незалежних змінних та функцій, входять похідні цих функцій. Такі рівняння називаються диференціальними та поділяються на два основних класи: звичайні (невідома функція є функцією однієї змінної) та рівняння у частинних похідних (невідома функція є функцією багатьох змінних). Розглянемо клас звичайних диференціальних рівнянь.

1. Диференціальним рівнянням називається рівняння, що пов'язує незалежну змінну х, шукану функцію у = f(х) та її похідні у', у", ..., у^(п): F (х, у, у', у", ..., у⁽ⁿ⁾) = 0

2. Порядком диференціального рівняння називається порядок найвищої похідної, що входить у рівняння.

3. Розв'язком диференціального рівняння називається  у = f(х), яка при підстановці в рівняння, перетворює його на тотожність. Процес відшукання розв`язку називається інтегруванням диференціального рівняння.

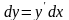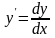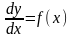
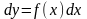
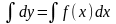
4. Найпростіше диференціальне рівняння першого порядку, розв'язане відносно похідної, у = f(х). Оскільки диференціал функції , то , підставляючи в рівняння, одержимо    y = F(x) + C.

5. Кожне диференціальне рівняння має нескінченну множину розв'язків, що відрізняються лише довільною сталою y = F(x) + C. Ця сукупність розв'язків називається загальним розв 'язком диференціального рівняння. Кількість довільних сталих загального розв'язку дорівнює порядку рівняння.

6. Якщо загальний розв'язок є неявною функцією відносно у: Ф ( у, х, С ) = 0, то він називається загальним інтегралом рівняння.

7. Надаючи довільній сталій С конкретних числових значень, одержимо частинні розв'язки диференціального рівняння, отже дістанемо нескінченну множину розв`язків. Графік частинного розв`язку диференціального рівняння називається інтегральною кривою цього рівняння. Усі інтегральні криві одного рівняння відрізняються лише сталим доданком, тому графічно загальний роз`язок утворює сім`ю паралельних кривих (рис. 8. 1). Для того, щоб із загального розв'язку одержати частинний, треба задати початкову умову, тобто вказати пару значень х та у : х = х₀, у = у₀.

8. Сумісне завдання диференціального рівняння та початкових умов, кількість яких дорівнює порядку рівняння, називається задачею Коші.

Геометрично розв`язати задачу Коші означає визначити єдину інтегральну криву, що проходить через задану точку площини (х₀; у₀).

9. Методи розв'язування диференціальних рівнянь першого порядку

9.1 Рівняння з відокремленими змінними

Диференціальне рівняння, в якому множник при dx є функцією, залежною тільки від змінної х, а при dy – залежною тільки від у, називається рівнянням з відокремленими

змінними.

 

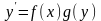
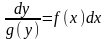
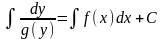
9.2 Рівняння з відокремлюваними змінними

Диференціальне рівняння, з якого шляхом елементарних алгебраїчних перетворень можна одержати рівняння з відокремленими змінними, називається рівнянням з відокремлюваними змінними.

 

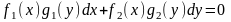
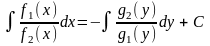
9.3 Однорідні рівняння

Функція f(х, у) називається однорідною, якщо t  0 виконується f(tx; ty) = f(x; y).

Диференціальне рівняння у' = f(х, у) називається однорідним, якщо функція f(х, у) є однорідною.

Однорідне рівняння зводиться до рівняння з відокремлюваними змінними за допомогою підстановки у = uх, де u = u(х), а х - незалежна змінна.

При цьому t = 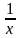, тоді f(х, у) = f(tх, tу) = f(1, u). Отже, рівняння у' = f(х, у) набуде вигляду u х + u = f(1, u).

9.4 Лінійні диференціальні рівняння

Диференціальне рівняння вигляду у' + р(х) у = q(х) називається лінійним рівнянням.

Лінійне рівняння зводиться до рівняння з відокремлюваними змінними за допомогою підстановки у = uv, де u = u(х), v = v(х) – певні функції, одна з яких довільна, друга визначається з рівняння. Підставляючи у = uv в рівняння, одержимо

u'v + v'u + р(х)uv = q(х)  u'v + u(v + р(х)v) = q(х)

Нехай v = v(x) – довільна. Виберемо її такою, щоб v' + р(х)v = 0  v = .

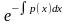З рівняння залишилось u'v = q(х)  u = .

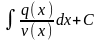Відповідь: у = uv = ( ) = ( ).

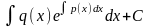9.5 Рівняння Бернуллі

Рівнянням Бернуллі називається рівняння вигляду у' + р(х) у = q(х)у^,   0;  1.

При  = 0 рівняння є лінійним, при  = 1 - з відокремлюваними змінними.

Рівняння Бернуллі зводиться до рівняння з відокремлюваними змінними за допомогою такої ж підстановки, як і лінійне