ЛІНІЙНА АЛГЕБРА

1. 1 Визначники

1. 1. 1 Короткі теоретичні відомості

Розглянемо квадратну таблицю чисел: 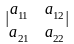. Кожний її елемент має вигляд а_ij, де і- номер рядка, j- номер стовпця, у яких розташований цей елемент.

1. Визначником 2-го порядку  називається число, що знаходиться з елементів таблиці за наступним правилом:  = а₁₁а₂₂ – а₁₂а₂₁.

2. Визначник 3-го порядку квадратної таблиці чисел 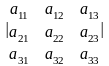знаходиться за формулою:  = а₁₁а₂₂ а₃₃ + а₁₂а₂₃а₃₁ + а₂₁а₃₂а₁₃ - a₁₃a₂₂a₃₁ - a₂₁a₁₂a₃₃ - а₃₂а₂₃а₁₁ ( правило Саріуса ). Цю формулу легко запам`ятати, користуючись схемою:

3. Мінором М_ij елемента а_ij визначника називається визначник, який утворюється з даного в результаті викреслення і-го рядка та j-гo стовпця.

4. Алгебраїчним доповненням А_ij елемента а_ij називається його мінор, взятий з відповідним знаком за формулою: .

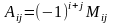5. Визначник n - го порядку квадратної таблиці чисел 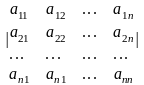знаходиться за наступним правилом:  = а_і1А_і1+ а_і2А_і2+...+ а_іnА_іn Цей метод називається розкладом визначника за елементами і-го рядка. Аналогічно можна обчислити визначник шляхом розкладу за елементами будь-якого стовпця. Користь цього метода полягає у зниженні порядку визначника.

6. Деякі властивості визначників:

1) у визначнику рядки та стовпці мають однакові властивості;

2) якщо у визначнику два рядки (стовпці) поміняти місцями, то визначник змінить знак;

3) якщо всі елементи деякого рядка (стовпця) нулі, то  = 0;

4) якщо визначник має два однакових або пропорційних рядка (стовпця), то  = 0;

5) спільний множник всіх елементів будь-якого рядка (стовпця) можна винести за знак ;

6) якщо кожний елемент і-го рядка (стовпця) є сумою двох доданків, то  дорівнює сумі визначників, у одного з яких і-й рядок (стовпець) складається з перших доданків, а у другого - з других;

7) визначник не зміниться, якщо до елементів одного рядка (стовпця) додати елементи іншого рядка (стовпця), помножені на одне й те саме число, відмінне від нуля.

Елементи теорії матриць

1. 2. 1 Короткі теоретичні відомості

1. Прямокутна таблиця чисел, складена з m рядків та n стовпців і записана у вигляді 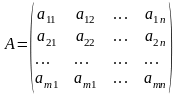або A = (a_іj), називається матрицею, де

a_іj - елемент матриці, і = 1, ..., m - номер рядка, j = l, ..., n - номер стовпця,

m x n - розмірність матриці.

Окремі випадки: m х 1 - матриця - стовпець, 1 х n - матриця - рядок, n х n - квадратна матриця, n - її порядок.

2. Множина елементів а₁₁, а₂₂, ..., а_nn називається головною діагоналлю матриці, a_n1, а_(n-1)2, ..., a_1n - допоміжною діагоналлю.

3. Квадратна матриця називається діагональною, якщо при i  j всі a_іj = 0, наприклад, діагональна матриця 3-го порядку: .

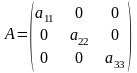4. Діагональна матриця називається одиничною , якщо при i = j всі a_іj = 1 і позначається Е. Наприклад, одинична матриця 3-го порядку: .

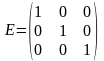5. Нульовою називається матриця, всі елементи якої a_іj = 0 і позначається О.

6. Транспонованою матрицею А^Т до матриці А називається матриця (a_іj)^Т= (а_ji), тобто рядки і стовпці якої міняються місцями.

7. Визначник є числовою характеристикою квадратної матриці. Квадратна матриця називається виродженою, якщо її визначник дорівнює нулю.

8. Дії над матрицями:

1) Множення на число: добутком матриці A_mxn = (a_іj) на число k (або k на А) , називається матриця В_mxn = (b_ij), де b_ij = ka_іj  i, j .

2) Алгебраїчна сума матриць визначена лише для матриць однакового розміру за правилом: С = А± В, де A_mxn = (a_іj), В_mxn = (b_ij), С_mxn = (с_ij): с_ij = a_іj  b_ij,  i, j.

3) Множення двох матриць визначено лише для узгоджених матриць.

Матриця A_mxn називається узгодженою з матрицею В_nхk , якщо кількість стовпців матриці А дорівнює кількості рядків матриці В. A_mxn  B_nxk = C_mxk. Квадратні матриці взаємно узгоджені.

Властивості:

1. А В  В А;

2. А Е = Е А = А;

3. А О = О А = О;

4. (k A)В = A(k B) = k(A B).

Правило множення: с_ij = a_i1 b_1j + a_i2 b_2j + ... + a_in b_nj , тобто кожний елемент с_ij дорівнює сумі добутків відповідних елементів і-го рядка матриці А та j-гo стовпця матриці В.

4) Ділення двох матриць можна розглядати як множення на обернену матрицю: 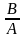= ВА^-1

Матриця А^-1 називається оберненою до матриці А, якщо виконується умова: АА^-1 = А^-1А = Е.

Для існування А^-1 необхідно і достатньо, щоб матриця А була невиродженою, тобто (А)  0, тоді обернена матриця знаходиться за формулою:

.

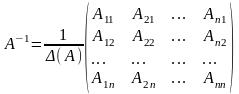Системи лінійних алгебраїчних рівнянь.

1. 3. 1 Короткі теоретичні відомості

1. Системою лінійних алгебраїчних рівнянь (СЛАР) називається система вигляду:

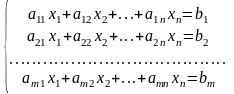, де

х_j - невідомі, j = 1,…, n;

а_ij – коефіцієнти при невідомих, i = 1,…, m;

b_i - вільні члени.

2. Упорядкований набір чисел Х = (х`<sub>1</sub>, х`₂ , ... , х`_n) називається розв 'язком СЛАР, якщо при підстановці його у систему всі рівняння перетворюються на тотожності.

3. СЛАР називається сумісною, якщо вона має принаймні один розв`язок, і несумісною, якщо не має жодного.

4. Сумісна система називається визначеною, якщо вона має єдиний розв`язок, і невизначеною, якщо більше одного.

5. Дві СЛАР називаються еквівалентними, якщо вони мають одну і ту ж саму множину розв`язків.

6. Елементарними перетвореннями СЛАР називаються такі перетворення, в результаті яких одержують еквівалентні системи, а саме:

1) переставлення місцями двох рядків;

2) множення кожного елемента рядка на одне й те саме число k  0;

3) додавання до елементів рядка відповідних елементів іншого рядка.

7. Система називається однорідною, якщо  b_i = 0.

8. Розв`язування СЛАР за формулами Крамера.

Метод застосовний лише для СЛАР з однаковою кількістю рівнянь та невідомих (і = j):

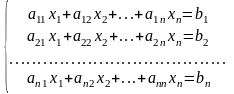
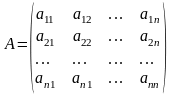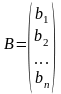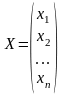Позначимо - основна матриця системи; - матриця-стовпець вільних членів, - матриця-стовпець невідомих.

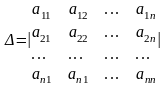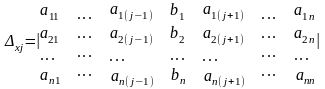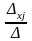За умови позначення основного визначника системи: , та допоміжних визначників: формули Крамера мають вигляд: х_j = , j = 1,…, n.

Можливі випадки:

1)   0, тоді СЛАР має єдиний розв'язок, який знаходиться за формулами Крамера. Якщо система однорідна, то цей розв'язок нульовий.

2)  = 0 і хоча б один _xj  0, тоді СЛАР несумісна.

3)  = 0 і всі _xj = 0, тоді СЛАР невизначена.

9. Розв'язування СЛАР матричним методом.

Метод застосовний лише для СЛАР з однаковою кількістю рівнянь та невідомих (і = j), основна матриця яких невироджена.

Матричний запис СЛАР: АХ = В, розв`язок знаходиться за формулою: Х = А^–1В

10. Розв'язування СЛАР методом Гаусса.

Метод застосовний для довільних СЛАР і грунтується на елементарних перетвореннях системи, спрямованих на те, щоб перетворити всі елементи нижче головної діагоналі на нулі. Перетворення доцільно проводити не з системою, а з розширеною матрицею системи: .

За допомогою елементарних перетворень розширену матрицю зводять до трапецієподібного вигляду:

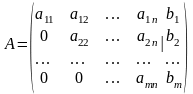
З останнього рядка знаходять х_n , підставляють у передостанній, знаходять х_n-1, і т.д. до 1-го рядка, з якого знаходять х₁.

ВЕКТОРНА АЛГЕБРА

2. 1 Дії з векторами