32. Основные элементарные функции комплексной переменной: степенная, целая рациональная, дробная рациональная, показательная, тригонометрические.

1) Степенная

Эта функция определена непрерывно и однозначно, на всей расширенной плоскости

2Целая рациональная функция или многочлен:

для любых

3 Дробно-рациональная функция

n<m

Эта функция определена непрерывно и однозначно для любых за исключением тех точек где знаменатель обращается в ноль

4. Показательная функция

Свойства:

1)

2 является переодической с T=2Пi, то есть

3. Функция является непрерывной на всей комплексной плоскости. Точка z= предела не имеет.

5_ Тригонометрические функции

33. Основные элементарные функции комплексной переменной: гиперболические, логарифмическая, обратные тригонометрические, обратные гиперболические.

Эти функции являются переодическими с периодом 2kпi.

Функция логарифмическая.

Обратные тригонометрические функции

Обратные гиперболические функции

34. Производная фкп. Условие Коши-Риммана.

Пусть функция определена в некоторой окрестности

Опр. Поизводной f(z) точки называется число равное пределу отношения при z

Если предел существует.

Функция имеющая производную в точке называется дифференцируемой в этой точке.

Функция f(z) называется дифференцируемой в области D если она дифференцируема в каждой точке этой области.

Из дифференцируемости функции f(z) в точке следует непрерывность функции в данной точке.

Правила нахождения производной ФКП

1. Если функции f(z) и g(z) дифференцируема в некоторой точке , то

2. Если функция w=f(z) имеет производную в точке z а функция w=F(w) имеет производную F’(w) в точке w=f(z), то сложная функция W=F(f(z)) дифференцируема в точке z.

W’=F’(w)*f’(z); w=f(z)

3. Если функция w=f(z) является взаимнооднозначной в окрестности точки и функция является обратной то:

Условие Коши-Рамана.

Если функцию w=f(z)=u(x;y)+iv(x;y), дифференцировать в точке , то функция u(x;y) и v(x;y) имеют первые частные производные в точке

35. Аналитические функции. Гармонические функции. Востановление аналитической функции по её известной действительной или мнимой части.

Однозначная функция f(z) называется аналитической в точке если она дифференцируема в самой точке так и в её окрестности.

Функция f(z) называется аналитической в точке если она аналитическая в каждой точке этой области.

Точка в которой функция f(z) является аналитической называется правильной точкой функции f(z) . Точка в которой функция f(z) не является аналитической или не определена называется особой точкой этой функции

Однозначная аналитическая функция f(z) называется регулярной.

Гармонические функции.

Пусть функция w=f(z)=u(xy)+iv(xy) является аналитической в некоторой области D причем u(xy) и v(xy) имеет непрерывные частные производные до второго порядка включительно.

Части аналитической функции f(z) удовлетворяют в области D уравнению Ла-Пласа.

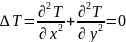
Действительные и мнимые части комплексной функции w=f(z) являются гармонической в области D функции.

U(x y) и v(x y) удовлетворяющие в области D условиям Коши Римана называются сопряженными.

Всякая гармоническая в односвязной области D функция служит дуйствительной(мнимой) частью некоторой аналитической в области D функции.