2. Передача теплоты через цилиндрическую стенку ( )

а) Граничные условия первого рода

Р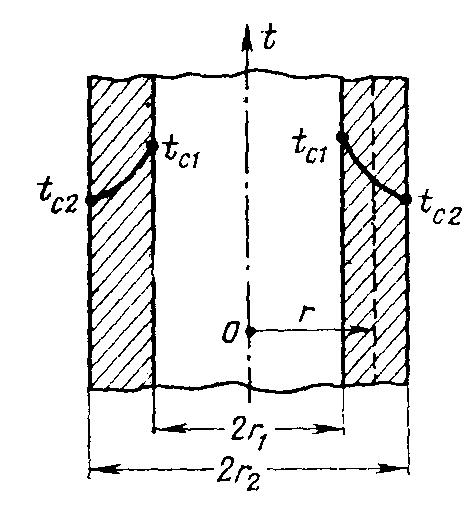 ассмотрим стационарный процесс теплопроводности в цилиндри­ческой стенке (трубе) с внутренним диаметром d₁=2r₁ и наружным ди­аметром d₂=2r₂ (рис. 2.6).

На поверхностях стенки заданы постоянные температуры t_с1 и tс2. В заданном интервале температур коэффициент теплопроводности ма­териала стенки λ является постоянной величиной. Необходимо найти распределение температур в цилиндрической стенке и тепловой поток через нее.

В рассматриваемом случае дифференциальное уравнение теплопро­водности удобно записать в цилиндрической системе координат

Рис. 2.6. Теплопроводность цилиндрической стенки.

. (2.34)

При этом ось Oz совмещена с осью трубы.

При заданных условиях температура изменяется только в радиаль­ном направлении и температурное поле будет одномерным. Поэтому

и . (а)

Кроме того, т.к. температуры на наружной и внутренней поверхностях трубы неизменны, изотермические поверхности являются цилиндрическими, имеющими с трубой общую ось. Тогда температура не должна изменяться также вдоль φ, т.е.

и . (б)

С учетом (а) и (б) уравнение (2.34) примет вид

. (2.35)

Граничные условия

п ри r = r₁ t = t_c1;

при r = r₂ t = t_c2. (2.36)

Если решить уравнение (2.35) совместно с (2.36), получим уравнение температурного поля в цилиндрической стенке.

Введем новую переменную

, (в)

тогда

. (г)

Подставляя (в) и (г) в уравнение (2.35), получим

. (2.37)

Интегрируя (2.37), получаем

. (д)

Протенцируя выражение (д) и переходя к первоначальным переменным, получаем

. (е)

После интегрирования получим

. (2.38)

Постоянные С₁ и С₂ можно определить, если в уравнение (2.38) подставить граничные условия

п ри r = r₁ t = t_c1, отсюда t_c1=С_1·lnr₁+C₂

при r = r₂ t = t_c2, отсюда t_c2=С_1·lnr₂+C₂ (ж)

Решение уравнений (ж) относительно С₁ и С₂ дает

.

Подставив значения С₁ и С₂ в уравнение (2.38), получим

или

. (2.39)

Полученное выражение представляет собой уравнение логарифми­ческой кривой. То обстоятельство, что распределение температуры в ци­линдрической стенке является криволинейным, можно объяснить сле­дующим.

В случае плоской стенки плотность теплового потока q остается одинаковой для всех изотермических поверхностей. По этой причине градиент температуры сохраняет для всех изотермических поверхно­стей постоянную величину. В случае цилиндрической стенки плотность теплового потока через любую изотермическую поверхность зависит от радиуса.

Для нахождения количества теплоты, прохо­дящего через цилиндрическую поверхность вели­чиной F в единицу времени, можно воспользо­ваться законом Фурье

.

Подставляя в уравнение закона Фурье зна­чение градиента температуры согласно уравне­нию (е), получаем (учитывая, что F=2π·r·l)

, (2.40)

здесь Q измеряется в ваттах.

Из уравнения (2.40) следует, что количество теплоты, проходящее через цилиндрическую стенку в единицу времени, полностью определя­ется заданными граничными условиями и не зависит от радиуса.

Тепловой поток (2.40) может быть отнесен либо к единице длины трубы, либо к единице внутренней или внешней поверхности. При этом расчетные формулы для плотности теплового потока, Вт/м², прини­мают вид

, (2.41)

(тепловой поток через единицу внутренней поверхности);

(2.42)

(тепловой поток через единицу наружной поверхности);

(2.43)

(поток теплоты, проходящий через единицу длины трубы, Вт/м).

Тепловой поток, отнесенный к единице длины трубы, измеряется в Вт/м и называется линейной плотностью теплового потока. Как видно из уравнения (2.43), при неизменном отношении d₂/d₁ линейная плотность теплового потока не зависит от поверхности цилин­дрической стенки. Плотности теплового потока q₁ и q₂ (отнесенные к внутренней и внешней поверхности) в случае передачи теплоты через трубу неодинаковы, причем всегда q₁ > q₂. Последнее ясно видно из уравнений (2.41) и (2.42).

Из уравнений (2.41)-(2.43) легко установит связь между величинами q₁, q₂ и q_l

. (2.44)

В случае, когда коэффициент теплопроводности является функцией температуры вида можно показать, что тепловой поток можно вычислить по той же формуле, что и для случая λ=const

. (2.45)

При этом следует помнить, что в формуле (2.45) λ_ср является среднеинтегральным значением коэффициента теплопроводности

.

Для нахождения температурного поля в случае можно воспользоваться уравнением закона Фурье, записанного для цилиндрической стенки

. (2.46)

Если разделить переменные и проинтегрировать уравнение (2.46) в пределах от r = r₁ до r и от t=t_с1 до t и найти из полученного интеграла t, получим выражение для температурного поля следующего вида

. (2.47)

б) Граничные условия третьего рода (теплопередача)

Рассмотрим однородную цилиндрическую стенку (трубу) с посто­янным коэффициентом теплопроводности λ. Заданы постоянные темпе­ратуры подвижных сред t_ж1 и t_ж2 и постоянные значения коэффициен­тов теплоотдачи на внутренней и наружной поверхностях труб α₁ и α₂ (рис. 2.7).

Н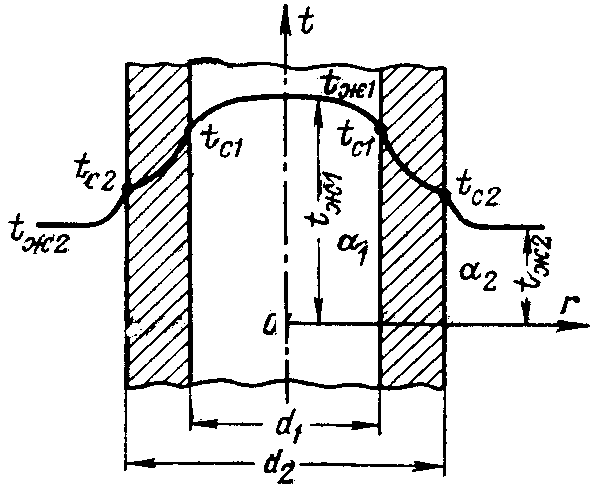 еобходимо найти q_l и t_c. Будем полагать, что длина трубы велика по сравнению с толщиной стенки. Тогда потерями теплоты с торцов трубы можно пренебречь, и при устано­вившемся тепловом режиме количество теплоты, которое будет передаваться от горячей среды к поверхности стенки, про­ходить через стенку и отдаваться от стенки к холодной жидкости, будет одно и то же.

Следовательно, можно написать

Рис. 2.7. Теплопередача через однородную цилиндрическую стенку.

(2.48)

Представим эти уравнения следующим образом

(2.48^/)

Складывая уравнения, входящие в систему (2.48^/), получаем температурный напор

.

Отсюда следует

. (2.49)

Обозначим

. (2.50)

С учетом (2.50) уравнение (2.49) запишется

. (2.49^/)

Величина k_l называется линейным коэффициентом теплопередачи, он измеряется в Вт/(м·К). Он характеризует интенсивность передачи теплоты от одной подвижной среды к другой через раз­деляющую их стенку. Значение k_l численно равно количеству теплоты, которое проходит через стенку длиной 1 м в единицу времени от одной среды к другой при разности температур между ними 1 град.

Величина R_l= 1/k_l, обратная линейному коэффициенту теплопере­дачи, называется линейным термическим сопротивлением теплопередачи. Она равна

, (2.51)

здесь R_l измеряется в м·К/Вт.

Отдельные составляющие полного термического сопротивления представляют собой

– термические сопротивления теплоотдачи на соответствующих поверхностях, обозначим их соответственно R_l1 и R_l2;

– термические сопротивления теплопроводности стенки, обозначим его через R_lс.

Следует отметить, что линейные термические сопротивления тепло­отдачи для трубы определяются не только коэффициентами теплоотда­чи α₁ и α₂, но и соответствующими диаметрами.

Если тепловой поток через цилиндрическую стенку отнести к внут­ренней или наружной поверхности стенки, то получим плотность тепло­вого потока, Вт/м², отнесенную к единице соответствующей поверхно­сти трубы

,

или

и

,

где .

Последнее соотношение устанавливает связь между коэффициентом теплопередачи при отнесении теплового потока к единице длины цилиндрической стенки и к единице поверхности

,

здесь k_l измеряется в Вт/(м·К).

Формулы же для k₁ и k_2, Вт/(м²·К), в развернутом виде имеют вид

. (2.52)

На практике часто встречаются цилиндры, толщина стенок которых мала по сравнению с диаметром. В этом случае при расчетах можно пользоваться упрощенными формулами. Для получения таких формул поступим следующим образом.

Величину разложим в ряд

Если отношение , то такой ряд сходится быстро, и с достаточной точностью можно ограничиться первым членом ряда

,

где δ – толщина цилиндрической стенки, м.

Подставив полученное значение в уравнение (2.52), получим

. (2.53)

Следовательно, если стенка трубы тонкая, то при практических расчетах можно пользоваться формулой

, (2.54)

где k, Вт/(м²·К), взят согласно формуле (2.53), т.е. как для плоской стенки. При этом, если d₂/d₁<2, погрешность расчета не превышает 4%. Для многих технических расчетов ошибка, не превышающая 4%, впол­не допустима. Обычно в инженерных расчетах при d₂/d₁≤1,8 пользуют­ся формулой (2.54).

Ошибку можно уменьшить, если в качестве расчетной поверхности в (2.54) брать поверхность, со стороны которой α меньше:

1. если α₁>>α₂, то d_x=d₂;

2. если α₂>>α₁, то d_x=d₁;

3. если α₁ ≈ α₂, то .

В случае теплопередачи через многослойную цилиндрическую стенку система равенства (2.48^/) должна быть заменена системой, учитывающей сопротивление теплопроводности всех слоев

(2.55)

После сложения равенства (2.55) и решения относительно q_l, Вт/м, получим

, (2.56)

или

. (2.56^/)

Величина

(2.56^//)

называется полным термическим сопротивлением многослойной цилиндрической стенки и измеряется в м·К/Вт.

Из уравнения (2.55) следует, что

(2.57)

В случае задания граничных условий первого рода их можно рассматривать как предельный случай граничных условий третьего рода, когда коэффициенты теплоотдачи на поверхностях α₁ и α₂ устремляются к бесконечности, в силу чего t_ж1 и t_ж2 становятся равными t_с1 и t_c(n+1). При этих условиях уравнение (2.56) принимает вид

, (2.58)

а выражение для расчета температуры на границах между слоями

. (2.59)