3. Тепловой поток. Закон Фурье

Необходимым условием распространения теплоты является нерав­номерность распределения температуры в рассматриваемой среде. Та­ким образом, для передачи теплоты теплопроводностью необходимо не­равенство нулю температурного градиента в различных точках тела.

Согласно гипотезе Фурье количество теплоты ,Дж, про­ходящее через элемент изотермической поверхности dF за промежуток времени , пропорционально температурному градиенту

. (1.8)

Опытным путем установлено, что коэффициент пропорциональности в уравнении (1.8) есть физический параметр вещества. Он характери­зует способность вещества проводить теплоту и называется коэффи­циентом теплопроводности.

Количество теплоты, проходящее в единицу времени через единицу площади изотермической поверхности , Вт/м², называется плот­ностью теплового потока. Плотность теплового потока есть вектор, определяемый соотношением

. (1.9)

Вектор плотности теплового потока направлен по нормали к изо­термической поверхности. Его положительное направление совпадает с направлением убывания температуры, так как теплота всегда пере­дается от более горячих частей тела к холодным. Таким образом, век­торы и лежат на одной прямой, но направлены в противопо­ложные стороны. Это и объясняет наличие знака «минус» в правых частях уравнений (1.9) и (1.8).

Л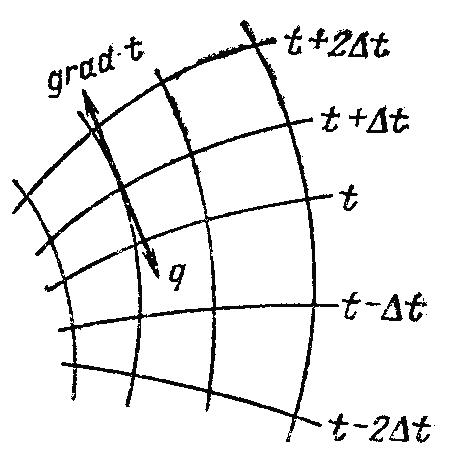 инии, касательные к которым совпадают с направлением вектора , называются линиями теплового потока. Линии теплового потока ортогональны к изотермическим поверхностям (рис. 1.2).

Скалярная величина вектора плотности теплового потока q, Вт/м², будет равна

. (1.10)

Рис. 1.2. Изотермы и линии теплового потока.

Многочисленные опыты подтвердили справедливость гипотезы Фурье. Поэтому уравнение (1.8), так же как и уравнение (1.9), явля­ется математической записью основного закона теплопроводности, ко­торый формируется следующим образом: плот­ность теплового потока пропорциональна гради­енту температуры.

Количество теплоты, проходящее в единицу времени через изотермическую поверхность F, называется тепловым потоком. Если гра­диент температуры для различных точек изотер­мической поверхности различен, то количество теплоты, которое пройдет через всю изотермиче­скую поверхность в единицу времени, найдется как

, (1.11)

где dF – элемент изотермической поверхности. Величина Q измеряется в ваттах.

Полное количество теплоты Q, Дж, прошедшее за время τ через изотермическую поверхность F, равно

. (1.12)

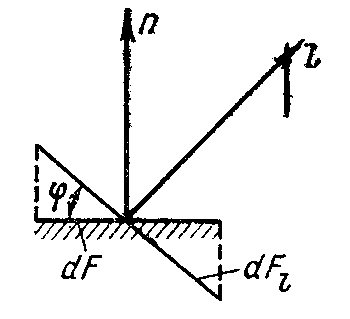
Количество теплоты, проходящее через элементарную площадку dF_l, расположенную под углом φ к плоскости, касательной к изотермической поверхности (рис. 1.3), определяется по той же формуле (1.12), если учесть, что

(1.13)

Рис. 1.3. К расчету теплового потока.

Так как является проекцией площадки dF_l на изотермическую поверхность, то количество теплоты, протекающее через элементарную площадку dF_l за время dτ, запишется как

. (1.14)

Общее количество теплоты, протекающее за время τ через поверхность F_l

. (1.15)

Из уравнения (1.13) следует, что самой большой плотностью теплового потока будет та, которая рассчитана вдоль нормали к изотермической поверхности. Если такой поток спроектировать на координатные оси Ох, Оу, Оz, то согласно уравнению (1.7) получим

; ; . (1.16)

Тепловые потоки, выраженные уравнением (1.16), являются составляющими вектора плотности теплового потока

. (1.17)

Из сказанного следует, что для определения количества теплоты, проходящего через какую-либо поверхность твердого тела, необходимо знать температурное поле внутри рассматриваемого тела. Нахождение температурного поля и является главной задачей аналитической теории теплопроводности.