7. Теплопередача через ребристую плоскую стенку

Необходимо найти тепловой поток через плоскую ребристую стенку безграничных размеров. Стенка оребрена со стороны меньшего коэффи­циента теплоотдачи (рис. 2.14).

З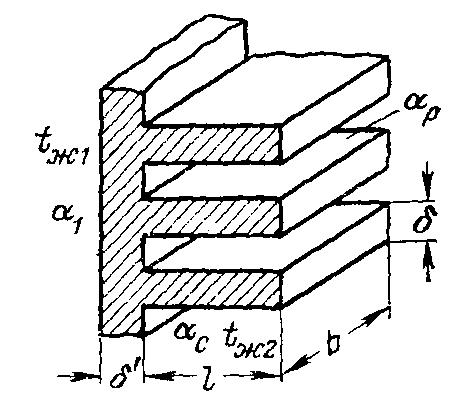 аданы постоянные значения коэффициентов теплоотдачи на не-оребренной поверхности стенки α₁, гладкой части оребренной поверх­ности α_с и на поверхности ребер α_р. Заданы геометрические размеры ребер (рис. 2.14) и температуры теплоносителей t_ж1 и t_ж2.

Поскольку для ребра b>>δ, то полагаем, что периметр поперечного сечения ребер u=2b. Площадь поперечного сечения ребра f=bδ.

С

Рис.2.14.Теплопередача через ребристую стенку.

ледовательно, , 1/м. Подставив полученное выражение для m в уравнение (2.75), умножив и разделив на 2l, получим

,

здесь – безразмерный комплекс, называемый числом Био.

Число Bi является важной характеристикой процесса теплопроводности. Оно представляет собой отношение внутреннего термического сопротивления теплопроводности к внешнему термическому сопротивлению теплоотдачи

.

Окончательно уравнение для теплового потока с поверхности ребра можно записать в виде

. (2.76)

Обозначим

.

Величина Е называется коэффициентом эффективности ребра. Тогда уравнение (2.76) принимает вид

.

Величина стремиться к своему максимальному значению, равному единице, при (при заданных геометрических размерах ребра последнее возможно в случае, если , т.е. ).

Теплота Q_c, Вт, отдаваемая гладкой частью оребренной поверхности

.

Общее количество теплоты

(а)

или

, . (б)

Из сопоставления (а) и (б) следует, что

(2.77)

Величина α_пр, входящая в уравнение (2.77), называется приведенным коэффициентом теплоотдачи. Это такой усредненный коэффициент теплоотдачи ребристой стенки, который учитывает теплоотдачу поверхности ребра, поверхности гладкой стенки и эффективность работы ребра.

Тогда для передачи теплоты через ребристую стенку можно записать систему уравнений

здесь δ^/ – см. рис.2.14.

Из этих уравнений получаем

. (2.78)

Если тепловой поток отнести к единице оребренной поверхности стенки, то

, (2.79)

где

– коэффициент теплопередачи через ребристую стенку при отнесении теплового потока к оребренной поверхности, Вт/(м²·К).

Если тепловой поток отнести к неоребренной поверхности стенки, то получим

, (2.80)

где

– коэффициент теплопередачи при отнесении теплового потока к неоребренной поверхности стенки.

Отношение оребренной поверхности F_р.с.к гладкой F₁ называется коэффициентом оребрения.

Влияние оребрения на коэффициент теплопередачи можно показать на следующем примере. Пусть α₁= 1000 и α₂ = 20 Вт/(м²·К). Предположим, что мало и им можно пренебречь, тогда

.

Для плоской поверхности (коэффициент оребрения F_р.с./F₁ равен единице) получим

Вт/(м²·К).

Если стенка имеет ребра с одной стороны, причем коэффициент F_р.с./F₁=2, то

Вт/(м²·К).

Следовательно, при заданных соотношениях коэффициентов теплоотдачи при оребрении плоской стенки со стороны малого α с коэффициентом оребрения F_р.с/F₁=2, передача теплоты увеличивается примерно в 2 раза.