№16 Основные правила и формулы дифференцирования.

Функция y=f(x) называется дифференцируемой в точке x₀, если ее приращение в этой точке можно представить в виде y =A*x+α(x)*x, где α(x) – бесконечно малая функция при стремлении x0. Так же дифференцируемая функция в точке - это функция, у которой в данной точке существует дифференциал.

Функция y=f(x) дифференцируема в точке x₀ тогда и только тогда, когда существует конечная производная функции в этой точке (f ‘ (x₀)).

Дифференциалом функции y=f(x) в точке x0 называется главная линейная относительноΔx часть приращения функции Δy в данной точке. (главная часть приращения функции это A*x)

Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:

(u±v)' = u'±v'

 Производная произведения двух дифференцируемых функций равна произведению первой функции на производную второй плюс произведение второй функции на производную первой, т. е.

(uv)' = u'v + uv'

 Производная частного двух дифференцируемых функций определяется формулой

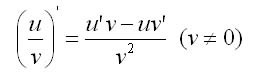
Таблица производных – учебник, доказательства в тетради.

Дифференциал суммы (разности) дифференцируемых функций равен сумме (разности) дифференциалов слагаемых:

d(u±v)=du ±dv

Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой:

d(uv) = udv + vdu.

Дифференциал частного находится по правилу

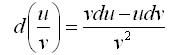
№17 Производная сложной и обратной функции. Производные функций, заданных параметрически. Производные неявно заданных функций.

Функция y=f(x) называется дифференцируемой в точке x₀, если ее приращение в этой точке можно представить в виде y =A*x+α(x)*x, где α(x) – бесконечно малая функция при стремлении x0. Так же дифференцируемая функция в точке - это функция, у которой в данной точке существует дифференциал.

Функция y=f(x) дифференцируема в точке x₀ тогда и только тогда, когда существует конечная производная функции в этой точке (f ‘ (x₀)).

Дифференциалом функции y=f(x) в точке x0 называется главная линейная относительноΔx часть приращения функции Δy в данной точке. (главная часть приращения функции это A*x)

Если монотонная функция f(x) в точке x₀ имеет производную f ’(x₀)≠0 тогда в некоторой окрестности точки x₀ существует обратная функция x=g(y) которая также имеет производную в соответствующей точке y₀=f(x₀), причем s ‘ (y₀) = 1/f ‘ (x₀).

Пусть функция  имеет производную в точке  , а функция  имеет производную в точке  . Тогда сложная функция   имеет производную в точке  , причем  .

Если функция f (x) задана параметрически x = φ(t), y = ψ(t), α < t < β,

где y = f(x) и функции φ и ψ дифференцируемы, причем φ'(t) ≠ 0, то .

Логарифмическое дифференцирование:

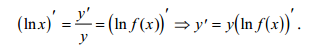
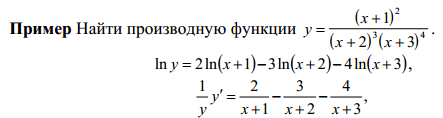
№18 Производные и дифференциалы высших порядков. Механический смысл производной второго порядка.

Производная функции в точке – это  предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю.

Функция y=f(x) называется дифференцируемой в точке x₀, если ее приращение в этой точке можно представить в виде y =A*x+α(x)*x, где α(x) – бесконечно малая функция при стремлении x0. Так же дифференцируемая функция в точке - это функция, у которой в данной точке существует дифференциал.

Функция y=f(x) дифференцируема в точке x₀ тогда и только тогда, когда существует конечная производная функции в этой точке (f ‘ (x₀)).

Дифференциалом функции y=f(x) в точке x0 называется главная линейная относительноΔx часть приращения функции Δy в данной точке. (главная часть приращения функции это A*x).

Дифференциал от дифференциала функции y=f(x) в данной точке называет дифференциалом второго порядка.

Дифференциалом порядка n, где n > 1 от функции    в некоторой точке называется дифференциал в этой точке от дифференциала порядка (n — 1).

dⁿ y

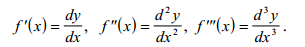
Производная от производной функции называет производной второго порядка. Вторая производная есть скорость изменения скорости, т.е. ускорение.

Производной n-го порядка от функции f (x) (n>1) называется производная первого порядка от производной (n-1) порядка функции f (x) при условии, что она существует.

- для заданной параметрически

Свойство инвариантности: дифференциал функции равен произведению производной этой функции на дифференциал аргумента, при этом безразлично будет ли этот аргумент независимой переменной или дифференцируемой функцией от другой переменной. ( для высших порядков не работает).

Применение дифференциала к приближенным вычислениям:

f(x) ≈ f(x₀) + f ' (x₀)·Δx.

Вычислить приближенно значение функции   в точке x = 17.

Пусть x₀= 16. Тогда Δx = x – x₀= 17 – 16 = 1,  ,

.

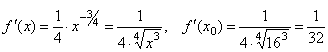Таким образом, 

№19 Теоремы о дифференцируемых функциях

Соответствие f, которое каждому элементу x множества X сопоставляет единственный элемент y множества У называется функцией.

В этом случае Х – область определения функции, У – область значений функции.

Способы задания функции:

1. Аналитический

2. Графический

3. Табличный

Функция y=f(x) называется дифференцируемой в точке x₀, если ее приращение в этой точке можно представить в виде y =A*x+α(x)*x, где α(x) – бесконечно малая функция при стремлении x0. Так же дифференцируемая функция в точке - это функция, у которой в данной точке существует дифференциал.

Функция y=f(x) дифференцируема в точке x₀ тогда и только тогда, когда существует конечная производная функции в этой точке (f ‘ (x₀)).

Теорема Ферма: пусть функция f(x) определена на (a,b), пусть в точке x₀ из этого интервала функция принимает наибольшее или наименьшее значение, пусть функция дифференцируема на этом интервале, тогда f ‘ (x₀) = 0. Геометрический смысл теоремы: в точках минимума и максимума функции касательная параллельна оси oX.

Теорема Ролля: пусть функция определена на [a,b], пусть функция непрерывна на этом отрезке и дифференцируема и интервале (a,b), а так же значение функции в точке a равно значению в точке b (f(a)=f(b)). Тогда существует c, принадлежащее этому отрезку, такое что , принадлежащее этому отрезку, такое что f ‘ (c) = 0.

Теорема Коши о среднем значении: если функции f и g непрерывны на отрезке [a; b] и дифференцируемы на интервале (а; b), причем g’(x) ≠ 0 на (а; b), то на интервале (а; b) существует такая точка с, что  .

Теорема Лагранжа: Формула конечных приращений Лагранжа выражает связь между приращением любой непрерывной на отрезке [a; b] и дифференцируемой на интервале (а; b)  функции y = f(x) и значением ее производной: где с – некоторое число из интервала (а; b): a < c < b.

Следствия из теоремы Лагранжа:

1. Если f ‘ (x) = 0 на некотором промежутке, то f(x) = const на этом промежутке.

2. Если 2 функции имеют равные производные на некотором промежутке, то эти функции отличны друг от друга на константу.