№8 Замечательные пределы.

Соответствие f, которое каждому элементу x множества X сопоставляет единственный элемент y множества У называется функцией.

В этом случае Х – область определения функции, У – область значений функции.

Способы задания функции:

1. Аналитический

2. Графический

3. Табличный

Пусть функция y=f(u) задана на множестве U и функция U=g(x) задана на множестве D, тогда говорят, что функция y=f(g(x)) определена на D и является сложной функцией.

Предел функции y=f(x) при хa

1. По Гейне ( на языке последовательностей):

Число А называется пределом функции y=f(x), при хa, если для любой последовательности аргументов сходящейся к а (х_na, n∞) соответствующая последовательность значений функции f(x_n) сходится к A.

2. По Коши ( на языке экселент-дельта (ε-δ)):

Число А называется пределом функции y=f(x), если при хa для любого ε>0 найдется такое δ(дельта)>0 такое что для любого х, удовлетворяющему неравенству |x-a|<δ, выполняется |f(x) – A|<ε.

Геометрический смысл определения предела функции:

Число А называется пределом функции y=f(x), если для любой ε-окрестности А найдется такая δ(дельта)-окрестность точки а, что для всех х≠а из этой дельта-окрестности соответствующие значения функции y=f(x) лежат в ε-окрестности точки А.

Предел функции y=f(x) при х+∞

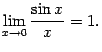первый замечательный предел

Теорема о втором замечательном пределе->  или  .

№9 Бесконечно малые и бесконечно большие функции. Сравнение

Соответствие f, которое каждому элементу x множества X сопоставляет единственный элемент y множества У называется функцией.

В этом случае Х – область определения функции, У – область значений функции.

Способы задания функции: Аналитический, Графический, Табличный.

Функция y=f(x) называется бесконечно малой функцией при xa, если lim f(x)=0, при xa.

Через определение предела:

Функция y=f(x) называется бесконечно малой функцией при xa, если для любого ε>0 найдется такое δ(дельта)>0 такое что для любого х, удовлетворяющему неравенству |x-a|<δ, выполняется |f(x)|<ε.

Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.

Произведение ограниченной функции на бесконечно малую функцию есть бесконечно малая функция.

Произведение двух бесконечно малых функций есть бесконечно малая функция

Произведение бесконечно малой функции на число есть бесконечно малая функция.

Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть бесконечно малая функция.

Сравнение б.м.ф.:

Говорят, что функция y=f(x) является в точке a бесконечно малой более высокого порядка, чем бесконечно малая функция y=g(x), если предел отношения f(x) к g(x) равен нулю (lim f(x)/g(x) = 0), при xa.

Говорят, что функции y=f(x) и y=g(x) являются в точке a бесконечно малыми одного порядка, если предел отношения f(x) к g(x) равен константе, и не равен нулю (lim f(x)/g(x) = const, ≠0), при xa.

Говорят, что функции y=f(x) и y=g(x) являются в точке a эквивалентными бесконечно малыми, если предел отношения f(x) к g(x) равен единице (lim f(x)/g(x) =1), при xa.

Говорят, что функция y=f(x) является в точке a бесконечно малой менее высокого порядка, чем бесконечно малая функция y=g(x), если предел отношения f(x) к g(x) равен бесконечности (lim f(x)/g(x) = ∞), при xa.

Если для любого сколь угодно большого числа N существует такое дельта зависящее от N (δ(N)), что при 0<|x-a|< δ(N) выполняется |f(x)|>N, то функция y=f(x) называется бесконечно большой при xa. (lim f(x) = ∞)

Если y=f(x) - бесконечно малая функция, отличная от нуля, то обратная функция 1/f(x) – бесконечно большая функция. Верно в обратную сторону.

Если функция f(x) имеет предел, равный A при xa, то ее можно представить как сумму числа A и бесконечно малой функции a(x) т.е. если lim f(x) = A, при xa, то f(x)= A+a(x), где lim a(x) =0, при a0. (верно и обратное).

Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой функцией.

Разность двух эквивалентных бесконечно малых функций есть бесконечно малая функция более высокого порядка, чем каждая из них. (справедливо обратное).

Сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.