№40 Понятие функции нескольких переменных.

Соответствие f, которое каждому элементу x множества X сопоставляет единственный элемент y множества У называется функцией.

В этом случае Х – область определения функции, У – область значений функции.

Способы задания функции:

1. Аналитический

2. Графический

3. Табличный

Переменная z называется функцией двух переменных x и y, если по некоторому закону каждой паре (x,y) из некоторого множества ставится в соответствие единственное определенное значение z. (Пусть f – соответствие, сопоставляющее каждой паре (x,y) единственное число z, тогда f – функция переменных (x,y))

x,y – независимые переменные, z- функция или зависимая переменная. D – область определения функции (множество всевозможных упорядоченных пар (x,y))

z=f(x,y).

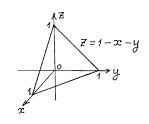
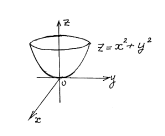
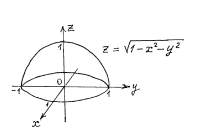
Геометрический смысл функции 2-х переменных – это поверхность в пространственной прямоугольной системе координат, являющаяся совокупностью всех произвольных точек M.

№41 Предел функции нескольких переменных.

Соответствие f, которое каждому элементу x множества X сопоставляет единственный элемент y множества У называется функцией.

В этом случае Х – область определения функции, У – область значений функции.

Способы задания функции:

1. Аналитический

2. Графический

3. Табличный

Переменная z называется функцией двух переменных x и y, если по некоторому закону каждой паре (x,y) из некоторого множества ставится в соответствие единственное определенное значение z. (Пусть f – соответствие, сопоставляющее каждой паре (x,y) единственное число z, тогда f – функция переменных (x,y))

x,y – независимые переменные, z- функция или зависимая переменная. D – область определения функции (множество всевозможных упорядоченных пар (x,y))

z=f(x,y).

Определение 1 (язык последовательностей):

Функция f(m) имеет пределом значение B при стремлении порознь координат точки m к соответствующим координатам точки A (mA), если для любой последовательности точек m₁,m₂…m_j, (где m_j ≠A, m_j € D) соответствующие значения функции f(m_j) сходятся к B.

B = lim f(m), при mA.

Определение 2 (язык экселент-дельта)

Функция f(m) имеет пределом значении B при стремлении переменных x₁,x₂…x_n к соответствующим значениям a₁…a_n, если для любого ε>0, существует δ>0 зависящее от ε, такое что для любых x₁,x₂…x_n удовлетворяющих неравенствам |x₁-a₁|<δ…..|x_n-a_n|<δ выполняется |f(x₁….x_n)-B|<ε.

Геометрический смысл предела: Пусть дана функция от двух переменных z=f(x,y), тогда для любого ε>0 существует δ-окрестность точки A с координатами (x_0­,y₀), такая что для любой точки M с координатами (x,y) из этой δ-окрестности значения функции отличаются от B не более чем на ε т.е. |f(x,y)-B|<ε.

B является пределом функции lim f(M), при M∞ , если для любого ε>0 существует такое a>0, что для любой точки М из области определения функции f(M) и такой что расстояние от нуля до M p(0,M)>a выполняется |f(M)-B|<ε.

Пусть f(M) и g(M) определены на множестве D. Пусть в точке A lim f(M) = B, lim g(M) = С, при MA.Тогда:

1. 1) Lim (f(M)±g(M))=B±C, при MA.

2. Lim (f(M)*g(M)) =B*C, при MA.

3. Lim (f(M)/g(M))=B/C, при MA.

Для повторных пределов функции сначала рассматривается предел для одной переменной, потом берется предел от полученного значения. Потом это делается наоборот. Примеры в тетради.

Lim Ψ(x) xx₀=lim_xx0(lim f(x,y)) yy₀.

Т. Если существует (конечный или бесконечный) двойной предел и при любом фиксированном   существует конечный предел , то существует и повторяющийся предел и он равен двойному пределу .