№32 Понятие определенного интеграла. Геометрический и физический смысл определенного интеграла. Необходимое условие интегрируемости функции.

Сумма вида

=f(ɛ₁)*x₁ +f(ɛ₂)*x₂ +….+ f(ɛ_n)*x_n

- интегральная сумма для функции у = f(x), соответствующая разбиению i_nотрезка [a,b] точками x₀, x₁,…, x_n (x₀=a, x_n=b).

Если существует предел интегральной суммы при стремлении диаметра разбиения к нулю (limσ_JI0), то его называют определенным интегралом от функции y=f(x) по отрезку [a,b].

Функция y=f(x) называется интегрируемой на отрезке [a,b], если для любой последовательности разбиений у которой предел диаметра разбиения стремится к нулю (lim JI_n=0, при n∞) соответствующая последовательность интегральных сумм сводится к одному и тому же числу, называемому определенным интегралом.

Необходимое условие интегрируемости: если f(x) интегрируема на [a,b], то она ограничена на [a,b].

Геометрический смысл: определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.

Так же можно вычислять с его помощью площади плоских фигур, длину дуги кривой, объемы тел, площади поверхности вращения, статистические моменты, моменты инерции, координаты центра тяжести,

Физический смысл определенного интеграла:

1. Работа переменной силы F , величина которой есть непрерывная функция F = F(x), действующей на отрезке [а; b], равна определенному интегралу от величины F(x) силы, взятому по отрезку [а; b].

2. Путь S, пройденный точкой за промежуток времени от t=а до t=b, равен определенному интегралу от скорости v(t):

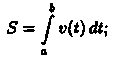
3. Масса m неоднородного стержня на отрезке [a,b] равна определенному интегралу от плотности g(х): .

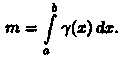4. Кинетическая энергия.

5. Давление жидкости.

№33 Классы интегрируемых функций.

Соответствие f, которое каждому элементу x множества X сопоставляет единственный элемент y множества У называется функцией.

В этом случае Х – область определения функции, У – область значений функции.

Способы задания функции:

1. Аналитический

2. Графический

3. Табличный

Функция y=F(x) называется первообразной для функции y=f(x) на отрезке [a,b], если производная функции F(x) равна функции f(x) ( F’(x)=f(x) ), для всех x из отрезка [a,b].

Классы:

1. Функция непрерывная на [a,b] интегрируема на [a,b].

2. Монотонная ограниченная функция на [a,b] интегрируема на [a,b].

3. Если ограниченная функция на [a,b] имеет конечное число точек разрыва, то она интегрируема на [a,b].

4. Если функция  f(x)  интегрируема на промежутке [a,b], то и функция  c f(x), где  c  – константа, интегрируема на этом промежутке.

5. Если функция  f(x)  интегрируема на промежутке [a,b], то и функция | f(x) | интегрируема на этом промежутке.

6. Если функции  f(x)  и  g(x)  интегрируемы на промежутке [a,b], то и их сумма, разность и произведение интегрируемы на этом промежутке.

7. Если функция  f(x)  интегрируема на промежутке [a,b], то она интегрируема и в любой части этого промежутка.

8. Если функция  f(x)  интегрируема в каждой части некоторого промежутка, то она интегрируема и на всем промежутке.