23. Принцип аргумента.

Пусть дан некоторый полином степени n По теореме Безу имеем:

Н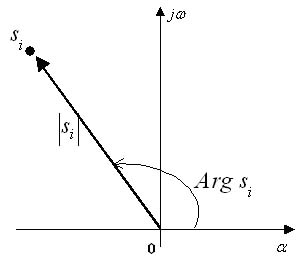 о комплексной плоскости s каждые корень данного полинома может быть изображен вектором таким образом, см. рис. слева.

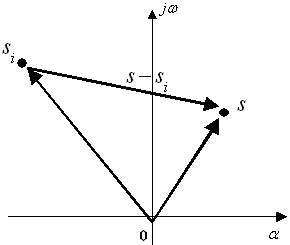
Величины (s-s_i) геометрически изображаются векторами, поведенными из точки s_i к произвольной точке s.

В частном случае, когда s = jω, получаем:

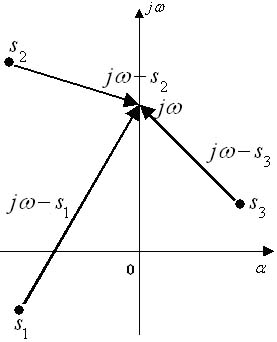
- вектор, равный произведению элементарных векторов и действительного числа a₀.

П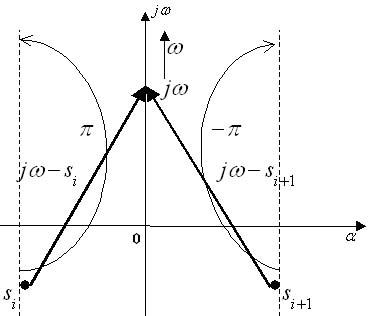 усть вращение против ЧС – положительное. Тогда при изм. ω от -∞ до +∞ каждый элементарный вектор повернется на угол π, если его начало лежит слева, и на –π, если справа.

Пусть полином P(s) имеет m правых корней и n – m левых. Тогда

Т.о. изменение аргумента P(jω) при изменении частоты от -∞ до +∞ равно разности между числом левых и правых корней уравнения P(s) = 0, умноженной на π.

Очевидно, что при изменении частоты от 0 до +∞ изменение аргумента вектора P(jω) будет вдвое меньше:

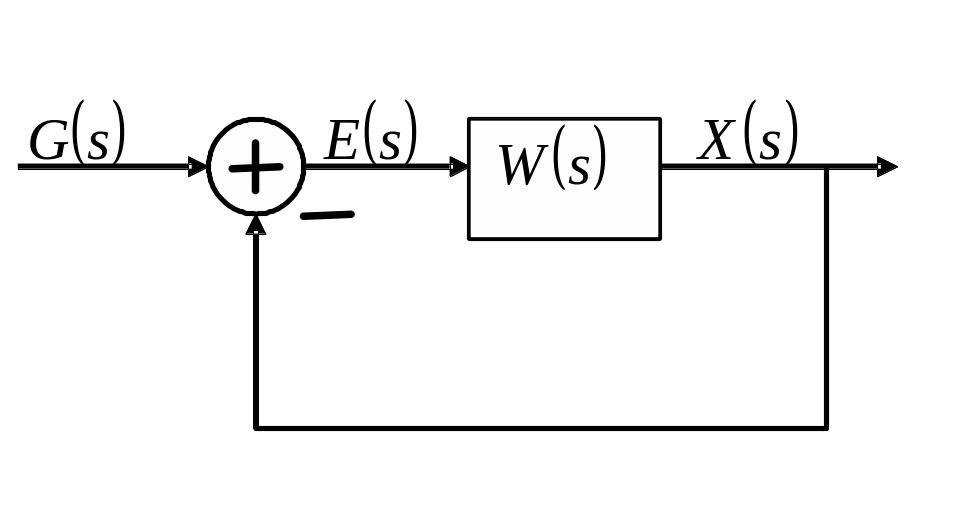
24. Частотный критерий Михайлова.

L(s) и M(s) – полиномы степени m и n, причем m<n.

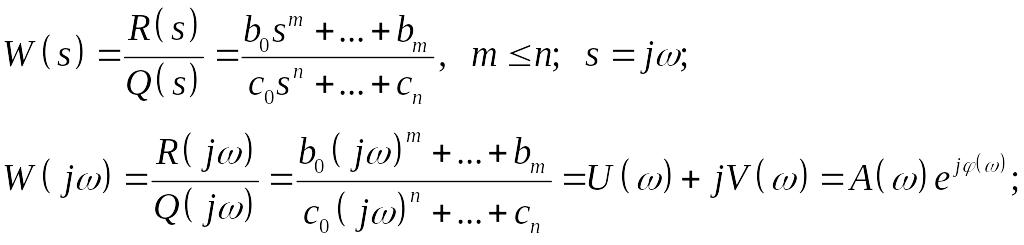
Хар. полином:

Михайлов сформулировал необход. и достат. усл-я устойч-сти ЗСАУ, которые получили название критерия устойч-сти Михайлова. Он позволяет, не решая хар. уравнения ЗСАУ , исследовать расположение его корней с помощью годографа Михайлова.

Критерий устойчивости Михайлова относится к частотным критериям и используется для исследования устойчивости замкнутых систем.

Ф-ии R(ω) и φ(ω) представляют собой модуль и аргумент P(jω).

П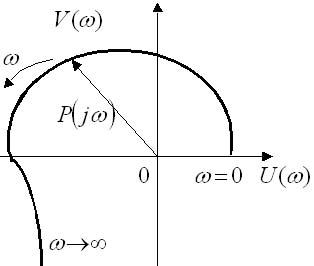 ри изменении частоты ω вектор P(jω) будет описывать своим концом на корд-ной плоскости некоторую кривую, кот. называется годографом Михайлова.

По принципу аргумента:

Отсюда определяем число корней полинома P(λ) с положит. действительными частями, т.е.

Из последнего равенства видно, что число корней P(λ) с полож. действит. частями m будет равно нулю при одном условии:

Это необход., но не достаточное условие устойчивости. Для устойч-ти сис-мы необход. и достаточно, чтобы все n корней хар. полинома имели отриц. действит. части, т.е. не должно быть корней, лежащих на мнимой оси и обращающих в нуль комплексный полином P(jω), т.е. должно выполняться еще одно усл-е:

Критерий устойчивости Михайлова: Для того, чтобы САУ была устойчива, необх. и дост., чтобы вектор кривой Михайлова P(jω) при изменении частоты ω от 0 до ∞ повернулся, нигде не обращаясь в нуль, вокруг начала координат против часовой стрелки на угол πn/2, где n - порядок хар. полинома сис-мы.

Замечание. Для устойч. ЗСАУ годограф Михайлова начинается при ω=0 на веществ. положит. полуоси U(ω), так как при a₀ > 0 все коэф-ты хар. полинома положительны и P(0)=a_n>0. Кроме того, для устойч. сис-м, описываемых обыкновенными дифурами с постоянными коэф-тами, аргумент φ(ω) комплексного числа P(jω) с ростом частоты ω должен возрастать монотонно, т.е. вектор P(jω) должен поворачиваться только против ЧС. Это следует из того, что с ростом частоты монотонно возрастают имеющие одинаковые (положит.) знаки аргументы элементарных векторов (jω–s_i), кот. являются слагаемыми аргумента вектора P(jω). Учитывая сказанное, критерий Михайлова:

Для того чтобы САУ была устойчивой, необх. и достат., чтобы годограф Михайлова при изм. ω от 0 до ∞, начинась при ω=0 на вещественной полуоси, обходил только против ЧС последовательно n квадрантов корд-ной пл-ти, где n - порядок хар. полинома сис-мы.

Признаком неустойчивости системы является нарушение числа и последовательности, пройденных кривой Михайлова квадрантов координатной плоскости, вследствие чего угол поворота вектора P(jω) оказывается меньшим, чем πn/2.

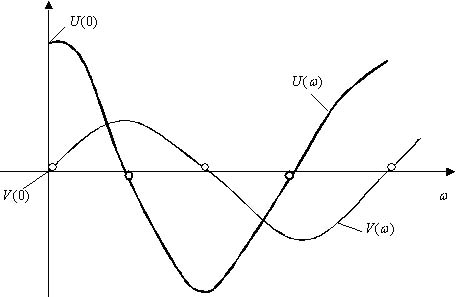
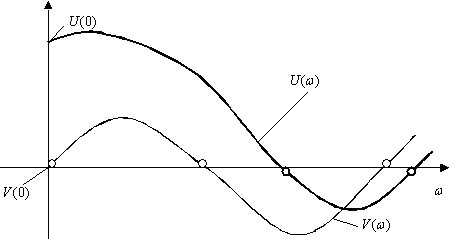
Анализируя годографы Михайлова, можно установить, что при последовательном прохождении кривой Михайлова квадрантов корд-ной пл-ти вещественная и мнимая оси пересекаются ею поочередно. В точках пересечения кривой Михайлова с вещественной осью обращается в нуль мнимая ф-ия Михайлова V(ω), а в точках пересечения с мнимой осью обращается в нуль вещественная ф-ия U(ω). Поэтому значения частот, при которых происходит пересечение кривой с вещественной или мнимой осью, должны являться корнями уравнений U(ω)=0 и V(ω)=0.

Вещественную U(ω) и мнимую V(ω) функции Михайлова можно представить графически в виде кривых: