21. Геометрический расчёт эвольвентных прямозубч цилиндрич передач

В зависимости от профиля зубьев колес различают зацепления трех основных видов: эвольвентные, когда профиль зуба образован двумя симметричными эвольвентами; циклоидальные, когда профиль зубьев образован циклоидальными кривыми; зацепления Новикова, когда профиль зуба образован дугами окружности.

Эвольвентой, или разверткой окружности, называется кривая, которую описывает точка, лежащая на прямой (так называемой производящей прямой) линии, касательной к окружности и перекатываемой по окружности без скольжения. Окружность, разверткой которой является эвольвента, называют основной окружностью. С увеличением радиуса основной окружности кривизна эвольвенты уменьшается. При радиусе основной окружности, равном бесконечности, эвольвента превращается в прямую, что соответствует профилю зуба рейки, очерченному по прямой.

Наиболее широкое применение находят зубчатые передачи с эвольвентным зацеплением, которое имеет следующие преимущества перед другими видами зацепления: 1) допускается небольшое изменение межосевого расстояния при неизменном передаточном отношении и нормальной работе сопряженной пары зубчатых колес; 2) облегчается изготовление, так как одним и тем же инструментом можно нарезать колеса

Приведенные ниже сведения относятся к эвольвентному зацеплению.

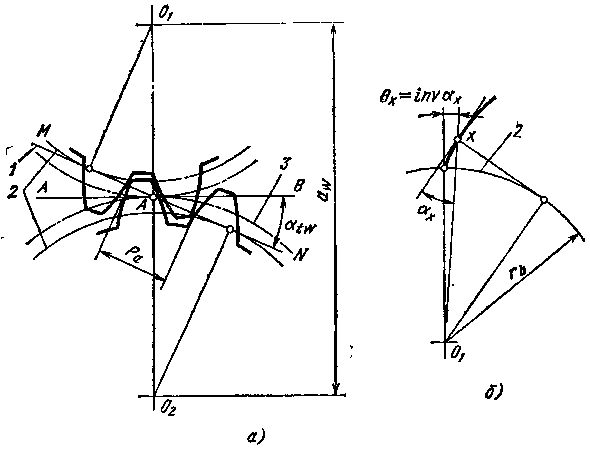
Схема звольвентного зацепления (рис. 3, а). Два колеса с эвольвентными профилями зубьев соприкасаются в точке А, находящейся на линии центров О1О2 и называемой полюсом зацепления. Расстояние aw между осями колес передачи по межосевой линии называют межосевым расстоянием. Через полюс зацепления проходят начальные окружности зубчатого колеса, описанные вокруг центров О1 и О2 и при работе зубчатой пары перекатывающиеся одна по другой без скольжения. Понятие о начальной окружности не имеет смысла для одного отдельно взятого колеса, и в этом случае применяют понятие о делительной окружности, на которой шаг и угол зацепления колеса соответственно равны теоретическому шагу и углу зацепления зуборезного инструмента. При нарезании зубьев методом обкатки делительная окружность представляет собой как бы производственную начальную окружность, возникающую в процессе изготовления колеса. В случае передачи без смещения делительные окружности совпадают в начальными. а — основные параметры; б — инволюта; 1 — линия зацепления; 2 — основная окружность; 3 — начальная и делительная окружности

22. Шпоночные соединения

Шпо́ночное соедине́ние — соединение охватывающей и охватываемой детали для передачи крутящего момента с помощью шпонки. Шпоночное соединение позволяет обеспечить подвижное соединение вдоль продольной оси. Классификация соединений в зависимости от формы шпонки: соединения призматическими шпонками, соединения клиновыми шпонками, соединения тангенциальными шпонками, соединения сегментными шпонками, соединения цилиндрическими шпонками. Шпонка представляет собой стальной брус, вставляе-мый в пазы вала и ступицы. Она служит для передачи момента между валом и ступицей колеса, шкива, звездочки. Основные типы шпонок стандартизированы.

Основной критерий работоспособности шпоночного соединения — прочность на смятие.

Достоинства шпоночных соединений:

• простота конструкции,

• легкость монтажа и демонтажа,

• низкая стоимость.

Недостатки шпоночных соединений:

• шпоночные пазы ослабляют прочность вала и ступицы,

• конструкция напряжений, возникающих в зоне шпоночного паза, снижает сопротивление усталости.

Шпоночные соединения подразделяются на:

• не напряженные: с использованием призматических и сегментных шпонок (при сборке в деталях не возни-кают предварительные напряжения);

• напряженные: с применением клиновых и тангенциальных шпонок (при сборке возникают монтажные на-пряжения).