14. Конструктивно-функциональная классификация механизмов.

Существует 5 осн. видов мех.: рычажные, кулачковые, фрикционные, зубчатые и мех. с гибкими звеньями.

Рычажные: их звенья обр. только вращ., поступ., цилиндр. и сферические пары.

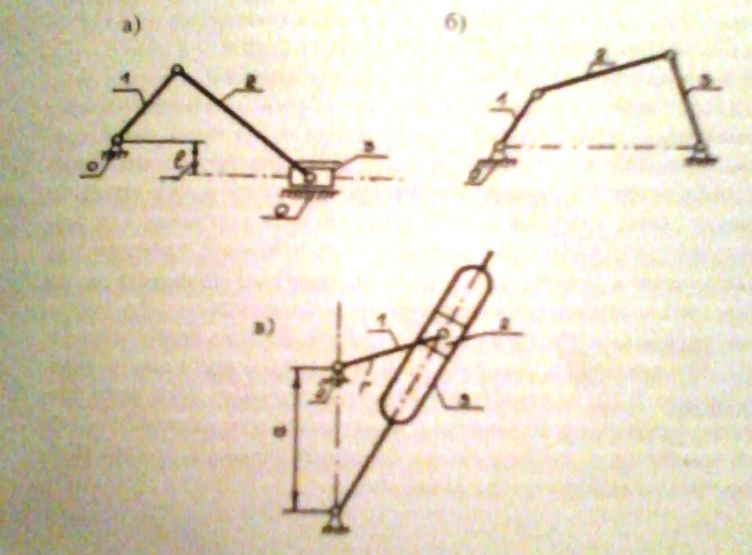
Кривошип 1- вращ. звено, кт может совершать полный оборот вокруг неподвижной оси. Шатун 2- звено, обр. кинемат. пары только с подвиж. звеньями. Ползун 3(рис. А) –звено, образ. поступ. пару со стойкой. Коромысло 3 (рис. Б) – вращ. звено, сов. только неполный оборот неподв. оси. Кулиса 3(рис. В)- звено, вращ. вокруг неподв. оси и образ. с др. подвижным звеном поступательную пару.

Кулачковые: мех. с кулачком. Кулачок – звено, им. элемент высшей пары в виде поверхности переменной кривизны. Предназначены для преобраз вращ. или вращ-пост. движ. кулачка в возвратно-вращ. или возвр.-пост. движ. толкателя.

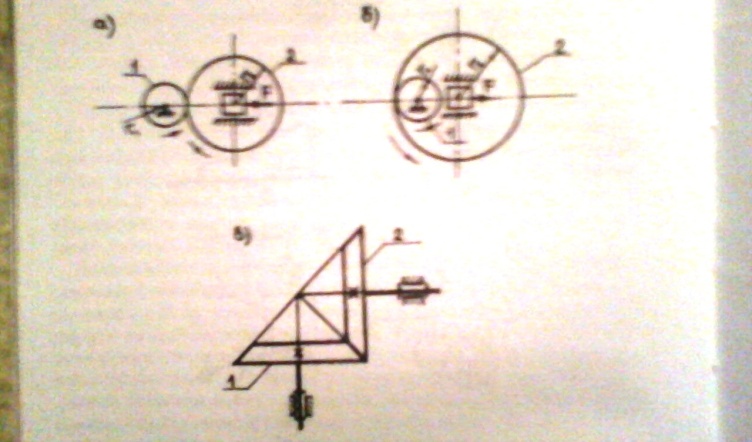
Фрикцинные: движ. от входного зв. к выходному перед. за счёт сил трения в местах контакта звеньев. Фрикционная передача с парал. (рис. А, б) или пересекающимися о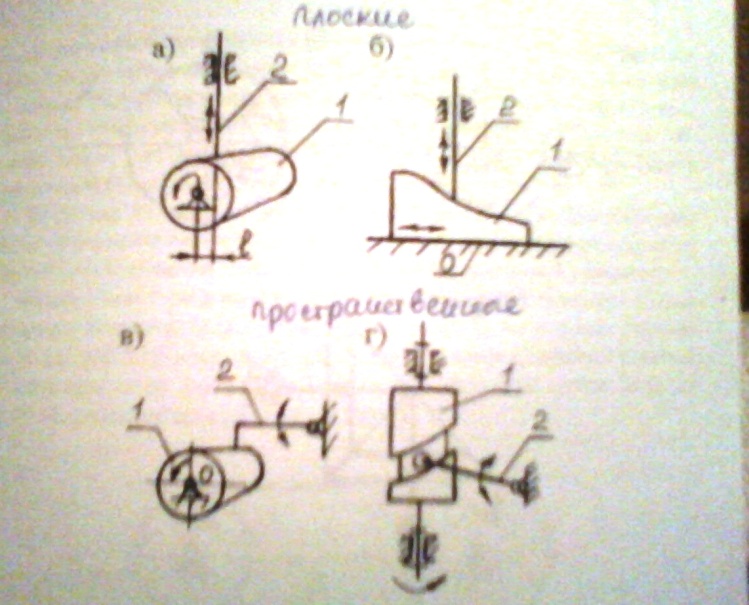 сями(рис.в).

Зубчатые: в составе зубчатые звенья. Зуб. звено- зв, им. звенья для передачи движ. посредством взаим. с выступами др звена. Зуб зацепление – высшая пара.

С гибкими связями: прим. для передачи вращ движ между валами при больших межосевых расстояниях.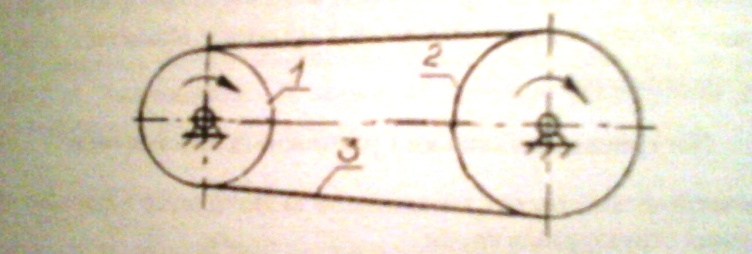

15. Профильные соединения.

Профильные соединения прим для передачи вращ М от вала к ступице. В профильных соединениях контакт вала и ступицы осущ по некруглой поверхности. Проф соед имеют в поперечном к оси соединения сечении плавный некруглый профиль поверхности контакта вала и ступицы. Чаще прим равноосные соед треуг профиля. Прим-ый профиль обладает св-ом равноосности – постоянством диаметрального размера. Проф соед в осевом направлении могут быть цилиндрическими или коническими (фасонно-проф соед-ия: а — по цилиндр пов, б — по конич пов.).

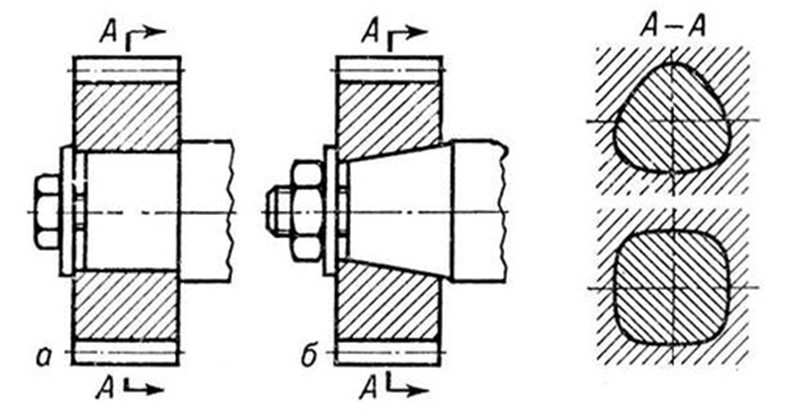
Достоинства профильных соединений: 1) отсутствие концентраторов напряжений кручения; 2) хорошее центрирование деталей соед; 3) повышенная надежность по критерию прочности соед по сравнению с соединениями с натягом.

профильных соединений: 1) сложность изготовления проф пов; 2) при передаче соед-ями вращ М возникают знач распорные силы, деформирующие ступицы.

16. Определение равнодействующей системы сходящихся сил методом проекций

Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определяем равнодействующую геоме­трическим способом. Выберем систему координат, определим про­екции всех заданных векторов на эти оси (рис. 3.4а). Складываем проекции всех векторов на оси х и у (рис. 3.46).

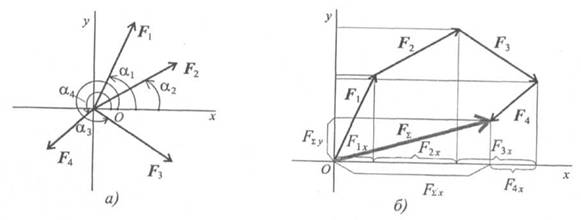
Рис.3.4

FΣч  = Flx + F2x + F3x + F4x; FΣн = Fly + F2y + F3y + F4y;

;   .

Модуль (величину) равнодействующей можно найти по известным проекциям:

  .

Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействую­щей с осями координат (рис. 3.5). Растяжение сжатиеПродольные силы и определение напряжений.

;

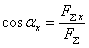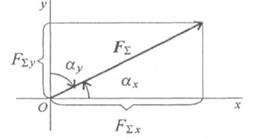
Рис.3.5

Условия равновесия плоской системы сходящихся сил в аналитической форме

Исходя из того, что равнодействующая равна нулю, получим:

  FΣ = 0.

Условия равновесия в аналитической форме можно сформулиро­вать следующим образом:

Плоская система сходящихся сил находится в равновесии, ес­ли алгебраическая сумма проекций всех сил системы на любую ось равна нулю.

Система уравнений равновесия плоской сходящейся системы сил:

.

В задачах координатные оси выбирают так, чтобы решение было наиболее простым.