11.Cложение пссс .Геометрическое условие равновесия пссс.

Система сил линии действия которых лежат в одной плоскости и пересекаются в одной точке ,такая система сил наз. ПССС.

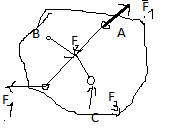
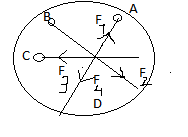
Если силы сходящихся сис-м приложены к разным точкам тела ,то по 1 следствию аксеомы статики каждую силу можно перенести в точку пересечения линиий действия и получить эквивалентную сис-му сил приложенных в одной точке.2 силы приложенные к одной точке тела образуют простейшую ПССС.

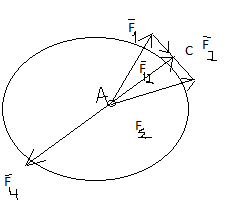
Порядок построения треугольника не влияет на результат. Чтобы уравновесить сис-му сил достаточно добавить к ней еще одну силу численно равную равнодействующей, но направленной в противоположенную сторону.

Геометрической форме необходимое и достаточное условие равновесия сис-мы СС: сис-ма СС уравновешена тогда, и только тогда, когда силовой треугольник замкнут.

12.Расчет на прочность стержней при растяжении-сжатии.

n= сигма пред./ сигма мах>=[n]

сигма мах- наибольшее расчетно напряжение.

В зависимости от цели расчета( постановки задачи) различают 3 вида расчетов на прочность:1) проверочный;2) проектный;3)определение допускаемой нагрузки. При проверочном расчете нагрузка бруса, его материал, его допускаемое или предельное напряжение и размеры известны. Определению подлежит наибольшее расчетное напряжение, которое сравнивают с допускаемым

Сигма мах= N/ A<=[сигма]

Сигма мах- напряжение возникающее в опасном поперечном сечении бруса.

Иногда при проверочном расчете удобнее сопоставлять не расчетное с допускаемым напряжением, а сравнивать рассчетный коэф-т запаса прочности для опасного сечения с требуемым: нагрузки материалов известны и тогда определяют требуемую площадь. Иногда проверочный расчет лучше вести в форме определения допускаемой нагрузки. Это целесообразно, когда возникает необходимость в повышении нагрузки существующего оборудования и тогда нужно знать их предельно допускаемое по условию прочности значение. Известны размеры бруса и материалы .Определяют значение продольно силы [N] с помощью методов сечения определения допускаемого значения внешних сил.

13. Продольная и попереч. Деформации. Закон Гука (при сжатии). Модуль упругости. Коэффициент Пуассона. Жесткость бруса.

Продольная деф. (относ. удлинение) – отношение прирощения (изменения) длины элемента к его первоначальной длине. ε =

Поперечная деф. – отношение измен. ∆а размера поперечного сечения к его первонач. значению.

ε’=

Зависимость между напряжением и продольной деформацией выражается законом Гука:

σ=Е*ε, где Е – модуль прод. упругости материала стержня, Н/м², ε- продольная деформация.

Модуль упругости – способность материала сопротивляться растяж. при упругих деф.

При растяжении (сжатии) в пределах упругих деформаций отношение поперечной деформации к продольной явл. постоянной для данного материала величиной. Модуль отношения наз. коэффициентом Пуассона: µ= .

Для различных материалов изменяется в пределах 0

Удлинение (укорочение):

∆l = , где ЕА – жёсткость стержня при растяжении(сжатии), l- длина участка бруса, м.