7.Перемещения и деформации.

Под действием внешних сил реальное тело деформируется. При этом первоначальное положение его сечений изменяется. Перемещения сечений вдоль прямой линии называются линейными, а перемещения, вызывающие поворот линий и плоскостей, - угловыми.

Деформация – характеристика интенсивности изменения линейных и угловых перемещений. Коэффициент податливости численно равен удлинению (упрочнению) бруса, вызванному силой, равной единице силы (1 Н или 1 кН). Если деформации тела исчезают после его разгрузки, их считают упругими, а неисчезающие деформации называют остаточными или пластическими.

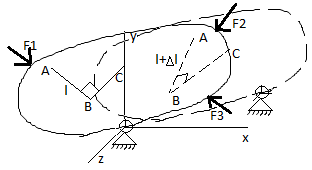
На поверхности тела некоторой точки прямой l, образующей отрезки АВ и ВС, после нагружения тела силами F1, F2, F3, деформируются, изменяются, а отрезки удлиняются на .

Предел отношения приращения длины отрезка его первоначальной длине называется относительной линейной деформацией.

Деформация направляющих координатных осей обозначается соответствующими индексами( )

Предел разности углов ABC и A’B’C’

- угловая деформация(угол сдвига) в т.В плоскости АВС.

В координатных плоскостях углы сдвига: ,

Т.о. в общем случае в точке имеют место 3 линейных и 3 угловых деформации.

Совокупность линейных и угловых деформаций по различным плоскостям, проходящих через данную точку, характеризуют деформирование состояния тела в этой точке.

8.Число степеней свободы(чсс) механизма. Подвижность механизма.

Если на движущиеся звенья в пространстве не наложено никаких связей, то ЧСС=6, тогда К звеньев, образующих кинематическую цепь до их соединения в кинематическую пару будут иметь 6К степеней свободы.

В общем случае кинематическая цепт может содержать 1-5 степеней свободы.

Общее ЧСС, наложенных всеми кинематическими парами, входящими в цепь:

5P₅+4P₄+3P₃+2P₂+1P₁

P_i- число пар i-го класса

ЧСС определяется по формуле:

H=6K-5P₅-4P₄-3P₃-2P₂-1P₁

H-число степеней свободы механизма.

При соблюдении определенных условий кинематическая цепь может стать механизмом.

Звенья кинем.цепи обладает определенностью движения только при наличии неподвижного звена.

Т.о. наличие неподвижного звена-обязательное условие существования механизма.

Степень подвижности механизма (пространственная) определяется по формуле Сомова-Малышева:

W=6n-5P₅-4P₄-3P₃-2P₂-1P₁

n-число звеньев

Cтепень подвижности(плоская) по формуле Чебышева:

W=3n-2P₅ – P₄

(сопромат)

9. Однородное растяжение бруса как пример реализации одноосного напряженного состояния материала. Центральное (осевое) растяжение/сжатие вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. В этом случае все внутр. силовые факторы, кроме фактора растягивающей/сжимающей силы, =0, т.е. возникает только один внутр. силовой фактор – продольная сила N_z/N. Прямые брусья, работающие на растяж./сжатие часто наз. стержнями. Продольные силы, соответствующие деформации растяжения,–знак+, деф.сжатия–знак–.

При растяжении прод. сила направлена от сечения, при сжатии – к сечению. Модуль и направление (знак прод. силы) опред. из ур-ния равновесия, составленного из отсеченной части бруса: ∑Z=0. N+∑F_iz=0 → N= –∑F_iz

Продольная сила в поперечном сечении бруса – равнодействующая внутренних нормальных сил, возникающих в этом сечении. N=σA

В тех случаях, когда прод. силы в различных поперечных сечениях бруса неодинаковы, закон их изменения по длине бруса предст. в виде графика – эпюра прод. сил (график ф-ции N=f(z)). Исп-ся при расчете прочности.

При растяжении/сжатии бруса, в его поперечных сечениях возникают только нормальные напряжения σ=N/A. При растяжении напряжение +, при сжатии–.

В местах резкого изменения формы и размера поперечного сечения бруса возникают местные напряжения – явление ”концентрация напряжения”. В тех случ., когда норм. напряжения в различных поперечных сечениях неодинаковы, целесообразно показывать закон их изменения по длине бруса в виде графика – эпюры норм. напряжений.

(теория механизмов и машин)

10.Структурный синтез и анализ механизмов. Структ.синтез механизма сост.в проектировании его структурной схемы(схема, указывающая стойку,подвижные звенья, виды кинематич. пар и их взаимное расположение).

Принцип Ассура. Более сложный рычажный механизм можно образовать путем присоединения открытых кинематических пар к исходному механизму. Мех-м, звенья кот. соединены с помощью низших кинем.пар – рычажный, стержневой. Структурная группа (группа Ассура) – кинематическая цепь, число степеней свободы которой =0 после присоединения ее внешними кинематич. парами к стойке, и которая не распадается на более простые цепи, удовлетворяющие этому условию.

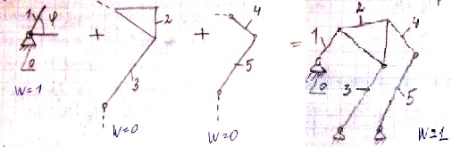
Для структурных групп плоских механизмов с низшими парами w=3n-2P_н (w – степень подвижности пространственного механизма,P_н – число звеньев; при w=0 P_н =3n/2)

n	2	4	6	…
Pн	3	6	9	…

Простейшая – структурная группа, у кот. n=2, P_н=3 – структурная группа 2го класса. Порядок структ.группы опред. числом элементов ее внешних кинемтических пар, которыми она может присоединяться к механизму. Все группы 2го класса явл. группами 2го порядка. Структ.группы, у кот. n=4, P_н=6 м.б. 3го или 4го класса. 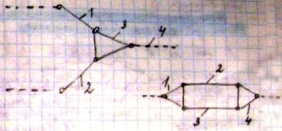В общем случае класс структ.группы опред.числом кинематич.пар в замкнутом контуре, образованном внутренними кинематич.парами. Класс механизма опред. высшим классом структ.группы, входящей в его состав.

Порядок образования механизма записывается в виде формулы его строения: I(0;1) →II(2;3)+ II(4;5) – механизм 2го класса(2й класс, 2 порядок, 1 вид).