40.Условие прочности при изгибе

Максимальное нормальное напряжение в балке возникает в сечении, где изгибающий момент достигает наибольшей по модулю величины, то есть в опасном сечении

.

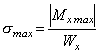Условие прочности при изгибе формулируется следующим образом: Балка будет прочной, если максимальные нормальные напряжения не превысят допускаемых напряжений

.

Величина допускаемых напряжений назначается в зависимости от материала, из которого изготовлена балка.

Пластичные материалы обладают примерно равными пределами текучести на сжатие   и на растяжение   равны между собой и поэтому  .

Для хрупких материалов, у которых прочность при сжатии выше, чем при растяжении, допускаемые напряжения на растяжение и сжатие, как правило, не равны между собой   и, поэтому, необходимо записывать два условия прочности

,             ,

где   и   - расстояния от нейтральной оси до наиболее удаленных растянутого и сжатого волокон.

Напряжения при поперечном изгибе

Нормальные напряжения, возникающие при поперечном изгибе, с достаточной для практических целей точностью могут определяться по формулам чистого изгиба. Поэтому условия прочности по нормальным напряжениям имеют тот же вид, что и для чистого изгиба.

Касательные напряжения в поперечных сечениях балки появляются при нагружении балки сосредоточенными и распределенными силами. Величина их определяется формулой Журавского:

,

где    - поперечная сила,

         - статический момент отсеченной части сечения относительно нейтральной оси,

        b - ширина сечения,

         - осевой момент инерции.

     Эпюра касательных напряжений показана на рис.6.6.

Условие прочности по касательным напряжениям будет иметь вид:

где   - наибольшая по модулю поперечная сила,

 - статический момент инерции верхней половины сечения.

Пусть в точке А абсолютно твердого тела приложена сила F. Выберем

центр приведения точку О (рис. а). Приложим в точке О силы F и — F

(рис. б). Перечеркнутые силы образуют пару с моментом:

M0<F)=rM*F,

где г0А

- вектор переноса силы. Эту пару можно перенести в любую точку

плоскости, содержащую силы F и — F, например точку О.

Таким образом, оказывается, что сила F приложена в точке О и к этой же

точке приложена пара с момнтом M0(F)=rAxF (рис. в).

41.Теория мех-ов и машин.2)Структура механизмов. Основные определения.

Механизм-система тел для преобразования одного или нескольких тв. Тел в требуемое движение других Машина- устройство, которое выполняет движения для преобразования энергии, материалов и информации с целью замены или облегчения физич. и умств. труда человека (Энергетич., Транспортные, технологич., информационные) Деталь- часть мех-ма, которую изготавливают без сборочных операций. Детали объединяют в узлы(сборочная единица, состоящ. из ряда деталей имеющих общее функц. назначение).Узлы могут содержть в себе мн-во подузлов Звено- одно(несколько)жёстко соедин. тел Стойка- неподвижное или приним. за неподвижные звенья. Из подвижных выдел.: Входное(звено, которое сообщ. Движение, преобразуемое мех-мом в движение др. звеньям), Выходное(звено, соверш. движ. для кот. Предназначен мех-м ) Промежуточные(остальные)

42.Теоретическая механика. Пространственная система сил. Условие равновесия парал-ых сил в пространстве. Равновесие протранств системы тв. тел. Простр. сист. сил- система сил, линия действия которой произвольно расположена в пространстве

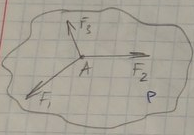Если к прилож. в точке А силе F1F2 добавить F3, нележащ. в плоск P…

Равновесие пространств системы тв. тел : Для равновесия тел при действии на него ПСС необходимо и достаточно, что бы гл вектор и гл М были = 0

В проекциях на коорд оси эти уравнения можно записать так: Т.е для равновес. тела в случ. действ. на него произвольной ПСС, необх и дост. что бы сумма проекций всех сил на кажд. из осей и суммы М этих сил относит. коорд . осей были = 0.