32. Условия прочности, коэффициент запаса прочности, допускаемые напряжения.

Конструкционные материалы можно разделить на 3 группы:

*пластинчатые

*хрупкопластинчатые

*хрупкие.

Механические испытания материалов позволяют определить не напряжения, при которых образец из данного материала разрушается илив нём возникают заметные пластинчатые деформации. Эти напряжения называются предельными(опасными). Отношение к пред. Напряжения к наиболее расчётному напряжению, возникающему в элементе конструкции при эксплуатационной нагрузке и называется коэффициентом запаса прочности:

n>1 n – устанавливаемое значение min необходимого запаса прочности

[n] – нормативный, требуемый запас прочности

Прочность элемента конструкции считается обеспеченой, если его расчётный коэф. Запаса проч-ти не ниже требуемого: n=>[n] -условие прочности

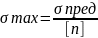
[ ]- допускаемое напряжение

Если предельное и допускаемое напряж при растяжении/сжатии различны, то их обозначения – [ ] [ ]

Пользуясь понятием допускаемых напряжений можно сказать, что проч-ть конструкции обеспечивается, если возникает в ней наиб напряж, не превышающих напряж

[ ] => max условие прочности

Существует 3 категории напряжения:

• Предельные(опасные) при достижении кот появляются признаки непосред. разрущения. Эти напряж зависят от св-в материала и вида деформации

• Допускаемые, кот можно допустить в расчётах конструкций из условий надёжности и долговечности. Они зависят от св-в, ида деформаций и требуем. Коэф. Запаса проч-ти

• Расчётные, кот возникают подд действием приложенных нагрузок. Зависят от действия нагрузок и их размеров.

13.Основные геометрические параметры цилиндрической зубчатой передачи

Межосевое расстояние и угол зацепления. В общем случае

определяют по формуле

где a = 0,5 (d1 + d2) – делительное межосевое расстояние;

- делительный угол профиля в торцовом сечении;

αtw – угол зацепления.

При заданном суммарном коэффициенте смещения для определения αtw

используют зависимость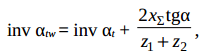

- суммарный коэффициент смещения;

Нулевой называют передачу, у которой x Σ = 0.

Косозубые передачи обычно выполняют нулевыми. В этом случае

Передаточное число. Это отношение числа зубьев колеса к числу

зубьев шестерни . В понижающих передачах передаточное число совпадает с передаточным отношением, по модулю равным отношению

угловых скоростей зубчатых колес, и потому .

Ширина зубчатых колес. Для большего колеса ширину зубчатого

венца вычисляют по формуле , где - коэффициент ширины зубчатого венца.

Величину ψba выбирают с учетом схемы расположения и типа зубчатых

колес: ψba = 0.315…0.5 - при симметричном расположении передачи

относительно опор; ψba = 0.25…0.4 - при несимметричном; ψba = 0.4…0.63 -

для шевронных и раздвоенных косозубых передач. Стандартные значения ψba

для редукторов: 0.16; 0.25; 0.315; 0.4; 0.5; 0.63; 0.8; 1.0.

Ширину зубчатого венца шестерни принимают на 2…5 мм больше bw2

для компенсации осевого смещения зубчатых колес из-за неточностей

сборки.

Диаметры окружностей зубчатых колес.

Делительные окружности d1 = mz1/cos β, d2 = mz2/cos β,

где β – делительный угол наклона зуба.

Основные окружности db1 = d1 cos α, db2 = d2 cos α .

Начальные окружности .

Окружности вершин и впадин зубьев:

daj = dj + 2m(1+ xj - Δy );

dfj = dj  2m(1.25 - xj),

где j = 1 для шестерни, j = 2 для колеса; xj – коэффициенты смещения;

Δy - коэффициент уравнительного смещения, Δy = x Σ -

Часть зуба, расположенную между окружностью вершин зубьев и

делительной окружностью, называют головкой зуба и обозначают ha Часть

зуба, расположенную между окружностью впадин зубьев и делительной

окружностью, называют ножкой зуба и обозначают hf. Для нулевых передач

ha = m, hf = 1,25 m.

Коэффициенты смещения. Смещение инструмента при нарезании

зубчатых колес производят для повышения прочности и износостойкостизубьев, а также для улучшения качественных показателей зацепления. Если

число зубьев колеса z<zmin, то при отсутствии смещения происходит

подрезание профиля зуба у его основания. Здесь zmin минимальное число

зубьев колеса без смещения, при котором не происходит подрезание. В

случае нарезания зубьев реечным инструментом для прямозубых передач

zmin=17, для косозубых передач определяется по формуле zmin= . Для

исключения подрезания при z<zmin коэффициент смещения должен

удовлетворять условию x ≥ 1 - .

Коэффициенты перекрытия. Важной характеристикой качества

зацепления является коэффициент торцевого перекрытия εα, равный

отношению угла поворота зуба в процессе зацепления к угловому шагу 2π/z.

В прямозубых передачах должно выполняться условие εα>1.1. Величину εα

определяют по формуле ,

где pbt – основной окружной шаг, αai = arccos .

В косозубых передачах вводится понятие коэффициента осевого

перекрытия

где px – осевой шаг зубьев; bw – ширина зубчатого венца.

Суммарный коэффициент перекрытия

εν = εα + εβ.

При проектировании косозубых передач рекомендуется подбирать такое

сочетание параметров, при котором выполняется условие εβ>1.1.

Точность зубчатых передач

Различают следующие основные показатели точности зубчатых

передач.

1. Кинематическая точность – характеризует наибольшую

погрешностью передаточного отношения или полную погрешность

угла поворота зубчатого колеса в пределах одного оборота.

2. Плавность работы – характеризует многократно повторяющиеся

циклические ошибки передаточного отношения или угла поворота

зубчатого колеса в пределах одного оборота.

3. Пятно контакта зубьев – характеризует распределение нагрузки по

длине зубьев, существенно влияет на работоспособность силовых

передач.