Бесконечно большие и бесконечно малые функции, сравнение бесконечно малых, связь между бесконечно малыми и бесконечно большими функциями.

Бесконечно малая последовательность — это последовательность, предел которой равен нулю.

Бесконечно большая последовательность — это последовательность, предел которой равен бесконечности. Последовательность an называется бесконечно малой, если 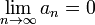Например, последовательность чисел 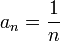— бесконечно малая. Функция называется бесконечно малой в окрестности точки x0, если 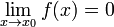Функция называется бесконечно малой на бесконечности, если 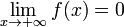либо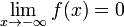 Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если 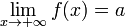то f(x) − a = α(x),

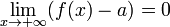
Бесконечно большая величина

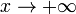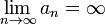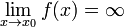Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция xsin x, неограниченная с обеих сторон, не является бесконечно большой при Последовательность an называется бесконечно большой, если Функция называется бесконечно большой в окрестности точки Функция называется бесконечно большой на бесконечности, если

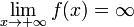
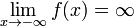
Свойства бесконечно малых

Сумма конечного числа бесконечно малых — бесконечно малая.

Произведение бесконечно малых — бесконечно малая.

Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.

Если an — бесконечно малая последовательность, сохраняющая знак, то 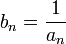бесконечно большая последовательность.

Сравнение бесконечно малых

Допустим, у нас есть бесконечно малые при одном и том же величины α(x) и β(x) (либо, что не важно для определения, бесконечно малые последовательности).

Если то β — бесконечно малая высшего порядка малости, чем α. Обозначают β = o(α).

Если 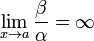то β — бесконечно малая низшего порядка малости, чем α. Соответственно α = o(β).

Если 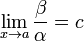(предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости.Это обозначается как β = O(α) или α = O(β) (в силу симметричности данного отношения).

Если 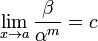(предел конечен и не равен 0), то бесконечно малая величина β имеет m-й порядок малости относительно бесконечно малой α.Для вычисления подобных пределов удобно использовать правило Лопиталя.

Примеры сравнения

При 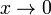величина x5 имеет высший порядок малости относительно x3, так как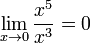 С другой стороны, x3 имеет низший порядок малости относительно x5, так как 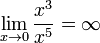С использованием О-символики полученные результаты могут быть записаны в следующем виде x5 = o(x3).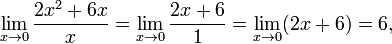

то есть при функции f(x) = 2x2 + 6x и g(x) = x являются бесконечно малыми величинами одного порядка.

В данном случае справедливы записи 2x2 + 6x = O(x) и x = O(2x2 + 6x).

При бесконечно малая величина 2x3 имеет третий порядок малости относительно x, поскольку 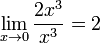бесконечно малая 0,7x2 — второй порядок, бесконечно малая 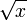— порядок 0,5.