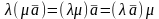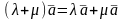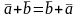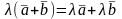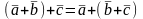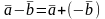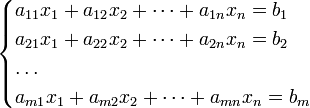10. Метод Гаусса решения слу:

Суть метода Гаусса заключается в

последовательном исключении неизвестных и состоит из двух этапов.

Прямой метод Гаусса (пошагово):

Выбирается одно из уравнений (оно объявляется ведущим). В этом уравнении выбирается ведущая переменная, в качестве которой может быть выбрана любая переменная с ненулевым коэффициентом.

С помощью равносильных преобразований эта переменная исключается из других уравнений системы.

Выбирается другое уравнение, которое объявляется следующим ведущим и т.д..

З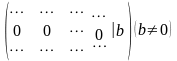 амечание 8.3. В ходе описанных преобразований можно получить систему, которой будет соответствовать расширенная матрица, содержащая нулевую строку. Наличие такой строки означает, что одно уравнение в исходной системе является линейной комбинацией остальных. Дальнейшие преобразования системы следует производить без данного уравнения (соответственно, без нулевой строки).

Замечание 8.4 На некотором этапе преобразований может быть полученарасширенная матрица следующего вида

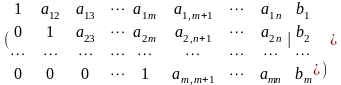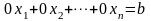В ыделенной строке этой матрицы соответствует уравнение , которому не удовлетворяет ни один набор чисел. Следовательно, система, в данном случае, несовместна.

Обратный ход метода Гаусса:

Последовательно, (начиная с последней) исключаются ведущие переменные (в записанной матрице им соответствуют единичные коэффициенты) из расположенных выше уравнений.

В результате всех преобразований (при условии совместности), будет получена система со следующей расширенной матрицей:

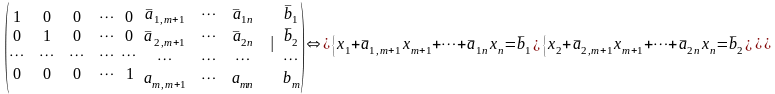(8.1)

Определение 8.3: Переменные x₁, x₂, …, x_m в системе (8.1) называются базисными, а х_m+1,…, x_n – свободными.

Замечание 8.4: Если в (8.1) m = n , то исходная система имеет одно решение (в этом случае свободные переменные отсутствуют)..

З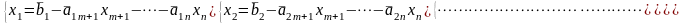 амечание 8.5: если в (8.1) n>m, то исходная система имеет бесчисленное множество решений, которые принято записывать в виде:

(8.2)

Придавая свободным переменным произвольные значения, можно получить, в соответствии с (8.2), всевозможные наборы чисел (x₁, x₂, … , x_n), удовлетворяющих исходной системе.

Пример 1. Решить систему линейных уравнений

x₁ + 2x₂ + 5x₃ = -9,

x₁ - x₂ + 3x₃ = 2,

3x₁ - 6x₂ - x₃ = 25.

Составим расширенную матрицу коэффициентов этой системы и с помощью элементарных преобразований приведем к ступенчатому виду:

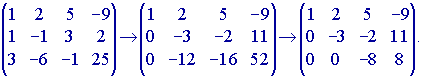
Мы приходим, следовательно, к системе уравнений

x₁ + 2x₂ + 5x₃ = -9,

      -3x₂ - 2x₃ = 11,

               -8x₃ = 8.

Система совместна и обладает единственным решением, т.е. определена. Находим решение полученной системы, начиная с последнего уравнения

x₁ = 2, x₂ = -3, x₃ = -1.

2. Основные понятия:

Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида

(1)

Здесь x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁, a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.

Система (1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (1) — совокупность n чисел c₁, c₂, …, c_n, таких что подстановка каждого c_i вместо x_i в систему (1) обращает все её уравнения в тождества.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c₁⁽¹⁾, c₂⁽¹⁾, …, c_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾, …, c_n⁽²⁾ совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

4. Векторная алгебра: основные понятия векторов, линейные операции над векторами и их св-ва, координатное выражение. Скалярное, векторное, смешанное произведения векторов: определение, св-ва, координатное выражение, приложения.

   1. Векторы, основные понятие и определения:

Величины, встречающиеся в физике, механике и других науках, можно разделить на 2 категории: скалярные (определяются числом) и векторные (определяются числовым значением и направлением). Вектораминаз-ся направленные отрезки. А – начало В – конецДлина вектора наз-ся его модулем.Вектор, начало и конец которого совпадают, наз-сянулевым.

Векторы, равные по модулю, параллельные, но направленные в противоположную сторону, наз-сяпротиволежащими.

Векторы, лежащие на одной или параллельных прямых, наз-сяколлинеарными.

Векторы а, в, с наз-сякомпланарными, если они лежат в одной плоскости или находятся в параллельных плоскостях.

Векторы наз-сяравными, если они имеют одинаковую длину и одинаковое направление.

Векторы, длина которых равна 1, наз-ся единичными векторами.

Свойства линейных операций над векторами: