Линейные алгебра и геометрия

1. Матрицы: основные понятия, алгебраические операции и их св-ва, ранг матрицы, элементарные преобразования.

Матрицей называется прямоугольная таблица чисел, состоящая из m строк и n столбцов. Числа m и n называются порядками матрицы

Обозначаются матрицы заглавными латинскими буквами (А, В, С,…), а элементы матриц малыми латинскими буквами с индексами (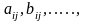 ). 1-й индекс - номер строки, 2-й индекс - номер столбца.

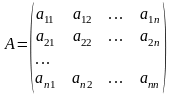
Матрицы равны между собой, если равны все их соответствующие элементы.

Матрица, у которой число строк и столбцов равно – называется квадратной.

Матрица, все элементы которой, кроме элементов главной диагонали равны нулю, называется диагональной.

Диагональная матрица, у которой все элементы главной диагонали равны 1, называется единичной. Обозначается буквой Е.

Матрица, у которой все элементы по одну сторону от главной диагонали равны нулю, называется треугольной.

Матрица, у которой все элементы равны нулю, называется нулевой.

1. Свойства матриц:

   1. Суммой двух матриц A=(a_ij) и B=(b_ij) с одинаковы количеством m строк и n столбцов называется матрица C=(c_ij), элементы которой определяются равенством A + B = C. Все элементы складываются.

   2. Произведением матрицы A=(a_ij) на число ƛ(лямбда) называется матрица, у которой каждый элемент равен произведению соответствующего элемента матрицы A на число ƛ: ƛA = ƛ(a_ij) = (ƛa_ij). число ƛ умножается на каждый член матрицы.

   3. Произведением матрицы A, имеющей m строк и k столбцов, на матрицу B, имеющую k строк и n столбцов, называется матрица C, имеющая m строк и n столбцов , у которой элемент c_ij равен сумме произведений элементов I-й строки матрицы A и j-го столбца матрицы B, т.е. c_ij = a_i1b_1j + a_i2b_2j +…+a_ikb_kj. При этом число k столбцов матрицы A должно быть равно числу строк матрицы B.

   4. Умножение на единичную матрицу. Матрица у которой все элементы равны нулю, кроме главной диагонали у которой все элементы равны единицы называется единичной матрицей и обозначается буквой E. Единичная матрица обладает свойством: умножение квадратной матрицы любого порядка на соответствующую единичную матрицу не меняет матрицу.

2. Рангом матрицы называется наивысший порядок отличного от нуля минора этой матрицы.

Обозначение:

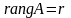
Минором эл-таа_ijназ-сяопр-ль матрицы, полученный из исходного опр-ля вычёркиванием i-ой строки и j столбца и обозн-ыйМ_ij.

Матрицы, имеющие одинаковый ранг наз-ся эквивалентными.

Т. е. надо получить нули ниже главной диагонали. И рангом будет являться количество ненулевых строк в матрице.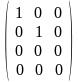

3. Элементарные преобразования:

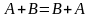
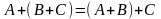
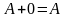
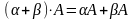
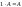
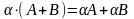
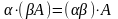
2. Определители второго и третьего, n-го порядка, св-ва определителей, вычисление обратной матрицы.

   1. Определителем (детерминантами) 3-го порядка, соответствующим матрице, называется число, обозначаемое символом (▲)

a₁₁a₁₂a₁₃

▲ = a₂₁a₂₂a₂

a₃₁a₃₂a₃₃

и определяемое равенством ▲ (слева +, справа - )

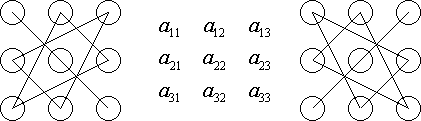
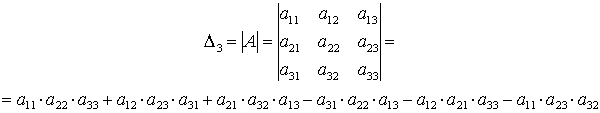
Пусть A квадратная матрица порядка n, n>1. Определителем квадратной матрицы A порядка n называется число

det A=   =  ,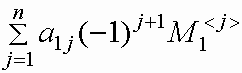