Задача №1
Такси обслуживает 3 населенных пункта. Вероятности того, что на остановке будут пассажиры (не более трех), желающих доехать до каждого пункта, соответственно равны 0.9, 0.85, 0.8. Составьте закон распределения числа пассажиров на остановке и вычислите числовые характеристики этого распределения. Какова вероятность того, что пассажиров будет не более двух?
Решение
X – число пассажиров на остановке |
0 |
1 |
2 |
3 |
P(X=m) |
|
0,056 |
0,329 |
0,612 |
Задача №2
Туристическое бюро, рекламируя отдых на одном из морских курортов, утверждает, что для этого курорта характерна идеальная погода со среднегодовой температурой +20 С. Пусть случайно отобраны 35 дней в году. Какова в этом случае вероятность того, что отклонение средней температуры за отобранные дни от среднегодовой температуры не превысит по абсолютной величине 2С, если температура воздуха распределена по нормальному закону, а стандартное отклонение дневной температуры составляет 4 С?
Решение.
n=35,
.
7
Задача №1
Интегральная функция распределения F(x) непрерывной случайной величины задана следующим образом.
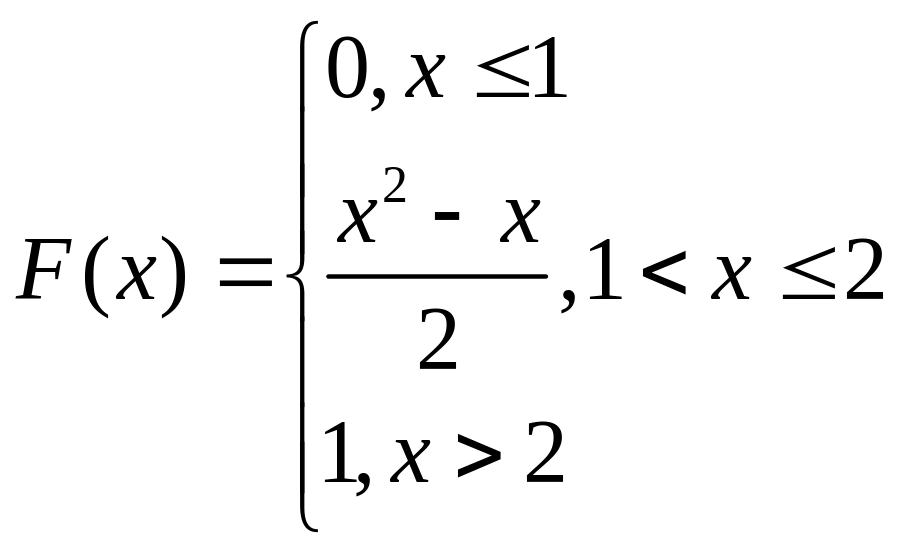
Найти плотность распределения этой случайной величины, вычислить числовые характеристики распределения и построить графики функции распределения и плотности распределения.
Задача №2
Предположим, что на некотором предприятии собраны данные о числе дней, пропущенных работниками по болезни.
Число дней, пропущенных в текущем месяце |
0 |
1 |
2 |
3 |
4 |
5 |
Число работников |
10 |
17 |
25 |
28 |
30 |
27 |
Построить полигон распределения частот. Найдите среднее число пропущенных дней, стандартное отклонение, коэффициент вариации. Является ли распределение симметричным?
8
Задача №1
Под руководством бригадира производственного участка работают 3 мужчин и 4 женщины. Бригадиру необходимо выбрать двух рабочих для специальной работы. Не желая оказывать кому-либо предпочтения, он решил выбрать двух рабочих случайно. Составьте ряд распределения числа женщин в выборке. Найдите числовые характеристики этого распределения. Какова вероятность того, что будет выбрано не более одной женщины?
Задача №2
Постройте гистограмму частот, найдите среднюю арифметическую, среднее квадратическое отклонение и коэффициент вариации для данных о дневной выручке в магазине электроники:
Выручка, у.е. |
0-200 |
200-300 |
300-400 |
400-500 |
500-600 |
600-700 |
Число дней |
3 |
5 |
9 |
14 |
8 |
3 |
9
Задача №1
Модельер, разрабатывающий новую коллекцию одежды к весеннему сезону, создает модели в зеленой, черной и красной цветовой гамме. Вероятность того, что зеленый цвет будет в моде весной, модельер оценивает в 0,3, что черный - в 0,2, а вероятность того, что будет моден красный цвет - в 0,15. Предполагая, что цвета выбираются независимо друг от друга, оцените вероятность того, что цветовое решение коллекции будет удачным хотя бы по одному из выбранных цветов?
РЕШЕНИЕ. 1 способ:
2
способ:
