Тема 2 – Методы и модели управления запасами

Цель: определить оптимальный размер партии закупки материалов.

2.1 Однопродуктовая статическая модель

В этой модели рассматривается запас одного материала. Интенсивность потребления запаса не меняется во времени, поэтому модель названа статической. В модели приняты следующие допущения:

- не допускается дефицит, т.е. уровень запаса не должен быть нулевым;

- пополнение запаса осуществляется мгновенно;

- цена на продукт не зависит от объема закупок.

Требуется определить размер партии закупки, при котором суммарные издержки, связанные с хранением запаса и оформлением договоров на поставку, минимальны.

Управляющей переменной является размер партии поставки.

Целевая функция – суммарные издержки.

Ограничений в задаче нет.

При заданных допущениях моделью динамики запаса является функция Y(t), график которой имеет «пилообразный» вид (рис. 9).

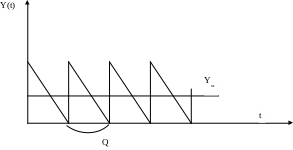
Рис. 9 График динамики запасов материалов

В модель введены следующие обозначения:

y – управляющая (искомая) переменная;

b – оценка интенсивности потребления запаса (const.);

Q – период кривой динамики запаса;

h – удельные затраты на хранение единицы продукции в единицу времени;

К – суммарные затраты на оформление договоров на поставку за период;

Y_sr – средний уровень запаса за период;

Z(y) – суммарные затраты, отнесенные к единице времени (целевая функция).

Для решения задачи необходимо выразить зависимость суммарных издержек от размера партии. При этом принимается во внимание следующее.

1. При постоянной интенсивности потребления величина запаса будет равномерно убывать. Время изменения запаса от начальной величины у до 0 будет равным периоду Q, т.е.

Q = y/b. (5)

2. Затраты на оформление сделки К за период следует пересчитать на единицу времени:

К_уд=K/Q=K/(y/b)=Kb/y. (6)

3. Так как величина запаса убывает линейно в течение периода, средний уровень запаса Y_sr=y/2. Затраты на хранение запаса объемом в у единиц в единицу времени будут равными:

Н(у)=hY_sr=hy/2. (7)

C учетом этих замечаний формируется целевая функция

Z(y)=K_уд + H(y)=Kb/y + hy/2. (8)

Задача состоит в нахождении такого у^`, при котором целевая функция достигает своего минимального значения. Такая задача может быть решена, как и любая задача на экстремум, путем дифференцирования и приравнивая производной к нулю:

dZ/dy= - Kb/y² + h/2=0,

y*=(2Kb/h). (9)

Полученная формула (9) называется формулой Уилсона для определения оптимального размера партии закупок.

Пример

Таблица 5 – Исходные данные

Величина	Значение
Суммарные затраты на оформление К, у.е.	70
Удельные затраты на хранение h, у.е.	5
Интенсивность потребления запасов b, шт./час	4

К_уд=Kb/y=280/y,

Н(у)=hy/2=5y/2,

y)=Kb/y + hy/2=280/y+ 5y/2 min.

Рис. 10 График суммарных затрат

Оптимальный (c наименьшими суммарными затратами) размер партии по графику составляет приблизительно 12 единиц. Точное значение размера партии может быть получено по формуле Уилсона (9).

у* =2Kb/h,4 единиц.

Индивидуальное задание I по теме 2:

- построить графики зависимостей от размера партии

- удельных затрат на оформление договора;

- затрат на хранение запаса;

- суммарных затрат;

- по графику определить примерную оценку оптимального размера партии;

- по формуле Уилсона рассчитать точное значение оптимального размера партии.

Таблица 6 – Варианты заданий

Показатель	Вариант
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
К	20	20	20	50	50	50	40	40	40	30	30	30	60	60	60
h	2	2	4	5	4	4	2	3	2	4	2	4	4	5	3
b	6	4	2	6	6	6	3	4	5	4	6	5	5	4	4

Продолжение табл.6.

Показатель	Вариант
	16	17	18	19	20	21	22	23	24	25	26	27	28	29
К	50	20	60	70	70	70	70	80	80	80	80	90	90	90
h	6	3	6	5	6	4	3	5	6	5	4	5	6	4
b	4	5	3	4	5	6	3	3	4	6	5	3	4	5

2.2 Однопродуктовая статическая модель с учетом снижения цены при оптовой продаже

В этой модели считаются выполненными все предположения первой модели, за исключением цены материала: цена зависит от размера партии поставки. Вид этой зависимости представлен на рис. 11.

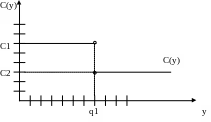
Рис. 11 Изменение цены при изменении объема закупки

При размере заказа, превышающем установленное поставщиком значение q1, сделка относится к категории оптовых и цена на единицу продукта меняется с величины С1 до величины С2. Это обстоятельство приводит к иному правилу выбора оптимального размера партии поставки.

В суммарных издержках Z(y) в этом случае следует учесть слагаемое, отражающее затраты на приобретение материалов. Обозначим это слагаемое через Р(у). Зависимость цены от размера партии можно представить в следующем виде:

С(у) = С1, если у  q1,

С (у) = С1, если у  q1. (10)

Затраты на приобретение партии материалов размером у будут равны величине

Р(у) = С(у)у, (11)

Эти затраты на единицу времени будут равными величине

Р(у) = С(у)у/t = С(у)b (12)

или с учетом вышесказанного

р(у) = С1b, если у  q1,

р(у) = С2b, если у  q1. (13)

С уммарные издержки в общем виде описываются выражением

Z(y) = p(y) + К_уд + Н(у) = C(y)b + Kb/y + hy/2 (14)

или с учетом вышесказанного

Z1(y) = C1b + Kb/y + hy/2, если у  q1,

Z2(y) = C2b + Kb/y + hy/2, если у  q1. (15)

В этих соотношениях слагаемые C1b и C2b не зависят от у и являются постоянными величинами. Графики функций Z1(y) и Z2(y) отличаются от графика зависимости Z(y)=K_уд + H(y) только смещением по вертикали на величины С1b и C2b соответственно. Точка минимума графиков при этом не меняет своего положения и определяется по формуле Уилсона.

Для определения оптимального размера партии в рассматриваемом случае следует использовать обе зависимости Z1(y) и Z2(y). Правило построения результирующей кривой суммарных затрат, минимум которой соответствует оптимальному размеру партии, следующее: отметить на оси у точку y = q1 и включить в результирующую кривую Z(y) на интервале (0,q1) участок кривой Z1(y), а на интервале [q1,∞) – участок кривой Z2(y).

Минимум этой сложной кривой зависит от положения точки y = q1, в которой происходит скачок значения цены. Для нахождения минимума следует вначале определить точку «равных затрат», которую обозначим через q2. В этой точке выполняется равенство Z2(q2) = Z1(y*), т.е.

C2b + Kb/q2 + hq2/2 = C1b + Kb/(y*) + h(y*)/2. (16)

В этом уравнении единственная неизвестная величина q2, которая может быть легко определена путем решения соответствующего квадратного уравнения. Предварительно следует определить значение у* по формуле Уилсона. Для дальнейшего анализа следует рассматривать большее значение из двух найденных корней квадратного уравнения.

Далее ось 0у следует разбить на 3 зоны:

1-я зона – (0,у*],

2-я зона – (y*,q2],

3-я зона – (q2,∞).

Правило определения оптимального размера партии с учетом затрат на приобретение материалов имеет следующий вид:

если q1 € (0,у*], то у_опт = у* (рис. 12),

если q1 € (у*,q2], то у_опт = q1* (рис. 13),

если q1 € (q2,∞), то у_опт = у* (рис. 14).

Рис. 12 Определение оптимального размера партии при q1 € (0,у*]

Рис. 13 Определение оптимального размера партии при q1 € (у*,q2]

Рис. 14 Определение оптимального размера партии при q1 € (q2,∞)

Пример

Таблица 7 – Исходные данные

Величина	Значение
Суммарные затраты на оформление К, у.е.	70
Удельные затраты на хранение h, у.е.	5
Интенсивность потребления запасов b, шт./час	4
Цена без скидки С1, у.е.	4
Цена со скидкой С2, у.е.	3
Размер партии, при котором сделка считается оптовой q1, шт.	15

По результатам расчетов примера первой части данной работы формула Уилсона дает значение у* = 10,54.

Найдем точку «равных затрат» q2. Для этого подставим в уравнение (16) известные величины, преобразуем его в квадратное уравнение и найдем его корни:

3*4 + 70*4/q2 + 5*q2/2 = 4*4 + 70*4/10,54 + 5*10,54/2

2,5q2 + 280/ q2 – 56,92 = 0

2,5 (q2)² – 56,92 q2 + 280 = 0

D = 56,92² – 4*2,5*280 = 3239,8864 – 2800 = 439,8864

q2_1,2 = (56,92±√D)/(2*2,5)

q2₁ = 15,58

q2₁ = 7,19

Так как 15 € (10,54; 15,58], т.е. q1 € (y*,q2], то у_опт = q1 = 15 (рис. 15).

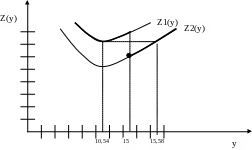
Рис. 15 Оптимальный размер партии закупки

Индивидуальное задание II по теме 2:

- рассчитать значения у* и q2;

- построить график функции суммарных затрат Z(y);

- определить оптимальный размер партии закупки материалов, подтвердить выбор графически.

При расчетах следует использовать результаты выполнения задания 1 и дополнительные данные из табл.8.

Таблица 8 – Варианты заданий

Показатель	Вариант
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
С1	2	4	4	2	2	2	3	3	3	2	3	3	3	3	2
С2	1	3	3	1	1	1	2	2	2	1	2	2	2	2	1
q1	15	20	10	15	15	15	20	10	10	10	20	10	20	15	10

Продолжение табл.8

Показатель	Вариант
	16	17	18	19	20	21	22	23	24	25	26	27	28	29
C1	3	3	4	4	4	3	3	3	4	4	2	2	4	2
C2	2	2	3	3	3	2	2	2	3	3	1	1	3	1
q1	15	20	15	20	15	20	15	10	15	20	20	15	15	20