6. Построение таблиц истинности логических выражений;

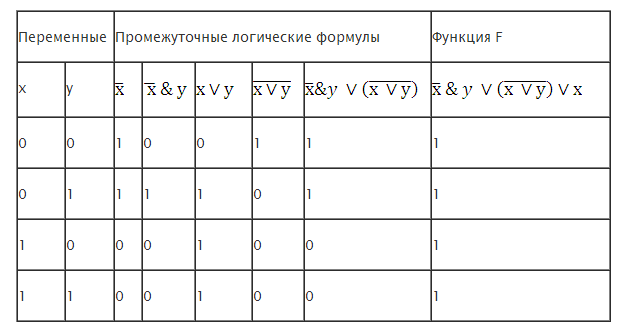
Таблица истинности логической формулы (функции) выражает соответствие между всеми возможными наборами значений логических переменных и значением функции. Для функции от двух переменных существует 22 = 4 комбинации наборов значений переменных, для функции трех переменных – 23 = 8, для функции четырех переменных – 24 = 16 комбинаций значений наборов переменных.

Последовательность построения таблицы истинности:

1. Определить количество N используемых переменных в логическом выражении.

2. Вычислить количество всевозможных наборов значений переменных M = 2^N , равное количеству строк в таблице.

3. Подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество логических операций.

4. Озаглавить столбцы таблицы названиями переменных и названиями логических операций.

5. Заполнить столбцы логических переменных наборами значений, например, от 0000 до 1111 с шагом 0001 в случае для четырех переменных.

6. Заполнить таблицу истинности по столбцам со значениями промежуточных операций слева направо.

7. Заполнить окончательный столбец значений для функции F.

Функции с двумя переменными 

7. Основные понятия теории множеств, операции над множествами;

Понятие множества является одним из основных неопределяемых понятий математики и служит для описания совокупности предметов или объектов. Эти объекты, или элементы множества, считаются отличимыми друг от друга и от объектов, не входящих в данное множество.

Отношение принадлежности . Тот факт, что объект a является элементом множества A, словесно выражается так: элемент a принадлежит множеству A. Обозначение: a A.

Отношение включения. Говорят, что множество B включено во множество A, если каждый элемент B принадлежит A. Обозначение: B A 

Подмножеством множества A называется всякое множество B, удовлетворяющее условию B A.

Множество, не содержащее ни одного элемента, называется пустым множеством. Обозначение: .

Пересече́ние мно́жеств в теории множеств — этомножество, которому принадлежат те и только теэлементы, которые одновременно принадлежат всем данным множествам.

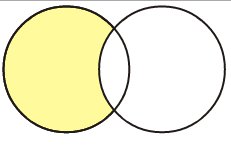
Объедине́ние мно́жеств (тж. су́мма илисоедине́ние) в теории множеств — множество, содержащее в себе все элементы исходных множеств.  

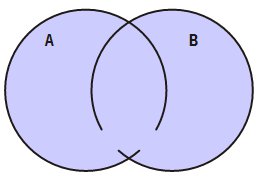
Разность двух множеств — это теоретико-множественная операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество.

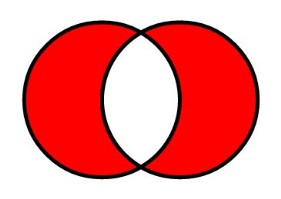
Симметрическая разность двух множеств — это теоретико-множественная операция, результатом которой является множество элементов этих множеств, принадлежащих только одному из них

8. Основные понятия теории графов.

ЗДЕСЬ ПРОСТАЯ КОПИПАСТА ЛЕКЦИИ, Я ЕСЛИ ЧЕСТНО САМ НЕ ДО КОНЦА ВКУРИЛ В ГРАФЫ, НАДО БУДЕТ ПОЧИТАТЬ КНИЖКУ НА ДОСУГЕ

Основные понятия

Граф задается парой множеств: множества Е, называемого мно­жеством вершин, и множества U, называемого множеством ребер. Ребро u U есть пара ( ), где , указывающая, между какими двумя вершинами проведено ребро. Говорят, что ребро ueU инцидентно вершинам . Если порядок ребер не имеет значения, т.е. u = ( ) = ( ), то ребро называется неориентированным или просто ребром, если же порядок имеет значение, то ребро u= ( ) называется ориентированным ребром или дугой. Вершина — назы­вается началом дуги, — конец дуги. Граф, содержащий хотя бы одну дугу, называется ориентированным графом или орграфом.

Граф G(E,U) называется конечным, если множество Е вершин конечно.

Граф G(E,U), у которого любые две вершины соединены ребром, называется полным. Если хотя бы две вершины соединены несколь­кими ребрами, то такой граф называется мулътиграфом. Две верши­ны называются смежными, если они соединены ребром. Чис­ло ребер, инцидентных данной вершине , называется локальной степенью этой вершины . Число ребер г графа G(E,U) определя­ется выражением

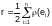количество вершин в графе.

Рассмотрим граф, изображенный на рис. 1.8.

Множество вершин графа состоит из пяти элементов: Е — {1, 2, 3, 4, 5}, а множество ребер U = {(1, 2), (1, 4), (1, 5), (2, 3), (3, 4), (5, 3)}. Ребро (5, 3) — является ориентированным ребром или дугой. Число ребер в графе определяется по значению локальных сте­пеней для каждой вершины:

Рис. 1.8. Ориентированный граф

.

Важным в теории графов является понятие части графа G(E,U), который обозначается

G'(E',U') G(E,U).

Множества вершин и ребер части графа являются подмножества­ми вершин и ребер исходного графа Е' Е U' U.

Многие задачи на графах состоят в определении частей графа с заданными свойствами.

Часть графа G'(E',U') G(E,U) называется подграфом графа G(E,U), если Е' Е , а подмножество U' U образовано только реб­рами, инцидентными вершинам множества Е'.

Полным графом называется граф G(E,U), у которого каждая вер­шина соединена ребрами с остальными вершинами (рис. 1,9).

Рис. 1.9. Полный граф

Связанность графов

Маршрутом графа G называется последовательность ребер 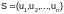, в которой каждые два соседних ребра имеют общую вершину, т.е. ; ; ... . Не исключено, что одно и то же ребро может встречаться несколько раз на одном маршруте.

Две вершины е. и е. называются связанными, если существует маршрут из е. в е..

Компонентой связности графа называется подмножество его вершин с инцидентными им ребрами, такое, что любая вершина связана с любой другой вершиной маршрута. Например, из графа на рис. 1.10 можно выделить следующие две компоненты связанности, показанные сплошной линией.

Рис. 1.10. Компоненты связанности графа

Простой цепью, или простым путем, называется маршрут, в котором ни одно ребро не повторяется дважды. Элементарной цепью или элементарным путем называется маршрут, в котором ни одна вершина не повторяется дважды. Циклом в графе называется маршрут, у которого начальная вершина совпадает с конечной. Например, следующий граф имеет цикл

S = (1, 2, 3, 5, 4, 1) (рис. 1.11).

Рис. 1.11. Цикл в графе

Цикл, проходящий по всем ребрам графа только один раз, на­зывается эйлеровым циклом. В теории графов доказывается теорема, определяющая, содержит ли граф эйлеров цикл. Оказывается, конеч­ный граф содержит эйлеров цикл тогда и только тогда, когда он свя­зан, и все его локальные степени вершин четные. Важной приклад­ной задачей теории графов является задача поиска в графе цикла, проходящего через каждую вершину только один раз. Такие циклы называются гамилътоновыми циклами.

Весьма важным является связанный граф, не имеющий циклов, он называется деревом. В дереве любые две вершины связаны един­ственным путем. Вершина называется концевой, если ей инцидентно не более одного ребра', одна из концевых вершин может быть выбрана в качестве корня.

Задание графа

Граф может задаваться в виде рисунка, аналитически, в виде матрицы. Выше приводилось задание графа в виде рисунка. Анали­тическое задание состоит в задании элементов множества вершин Е = { е₁, е₂, ... е_п} и множества ребер U = {u₁ ,и₂, ... u_m}.

Для выполнения различного рода формальных преобразований над графами удобно использовать их матричные задания. Матрица А размерностью n х n называется матрицей смежности графа G(E,U), если ее элементы образованы по правилу: элемент матрицы , если вершины и . соединены т ребрами, и , если эти вершины не связаны ребрами. Матрица смежности имеет число строк и столбцов, равное количеству вершин графа.

Матрица А размерностью n х m называется матрицей инцидентности графа G(E,U), если ее элементы образованы по правилу: элемент матрицы , если вершина е. инцидентна ребру в противном случае. Так как каждое ребро инцидентно двум вершинам, то в каждой строке этой матрицы ровно два ненулевых элемента.

Построим матрицы смежности и инцидентности для графа, изображенного на рис. 1.12.

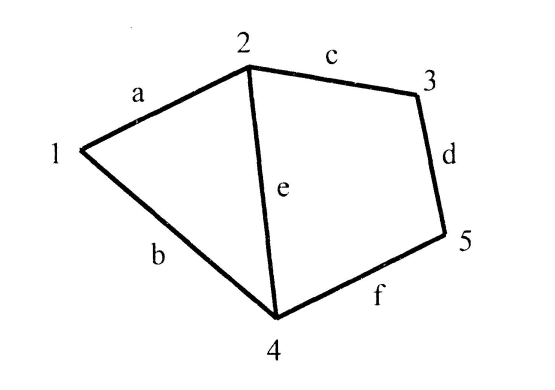
Рис. 1.12. Пример графа

Матрица смежности будет состоять из пяти строк и пяти столбцов.

1 2 3 4 5

1 0 1 0 1 0

2 1 0 1 1 5

3 0 1 0 0 1

4 1 1 0 0 1

5 0 0 1 1 0

Матрица инцидентности будет состоять из пяти строк и шести столбцов.

а b с d е f

1 1 1 0 0 0 0

2 1 0 1 0 1 0

3 0 0 1 1 0 0

4 0 1 0 0 1 1

5 0 0 0 1 0 1