1)Виды проецирования:

1)Центральное

Центральное проецирование – проецирующие лучи выходят из одной точки (центра). Размеры предмета на плоскости проекций искажаются (рис.1). 2) Параллельное

Параллельное проецирование – проецирующие лечи параллельны и составляют с плоскостью угол 90% (прямоугольное проецирование рис.2) и угол отличный от 90 % (косоугольное проецирование рис.3).

2)Свойства прямоугольного проецирования:

Свойства прямоугольного проецирования.

1. Точка проецируется в точку.

2. Прямая проецируется в прямую (в общем случае).

3. Если точка принадлежит прямой, то и проекция точки принадлежит проекции прямой.

4.Если прямые параллельны, то их проекции параллельны.

5. Отношение отрезков прямой равно отношению проекций этих отрезков.

6. Отношение отрезков параллельных прямых равно отношению проекций этих отрезков.

7. Проекция геометрической фигуры по величине и форме не изменяется при параллельном перемещении плоскости проекций.

8. Проекция отрезка не может быть больше самого отрезка.

3) Теорема о проецировании прямого угла.

Решение многих метрических задач требует применения перпендикулярных прямых и плоскостей и основывается на свойства прямоугольного проецирования прямого угла.

Прямой угол проецируется без искажения если обе стороны параллельны плоскости проекций. Если стороны угла не параллельны плоскости проекции, то угол проецируется с искажением на а эту плоскость проекции.

Теорему о проецировании прямого угла мы рассматривали при изучении свойств ортогонального проецирования. Напомним эту теорему.

Теорема:

Если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то угол на эту плоскость проецируется в натуральную величину. Следствие: если прямоугольная проекция угла, одна сторона которого параллельна плоскости проекций, - прямой угол, то проецируемый угол также прямой.

Свойства проекций прямого угла имеют важное значение при решении метрических задач на чертеже, таких, как построение взаимно перпендикулярных прямых и плоскостей определения расстояния между геометрическими фигурами и т.д.

4) Способ перемены плоскостей проекции

Решение позиционных и метрических задач становится проще, если геометрические фигуры находятся в частном положении относительно плоскостей проекций. Для того, чтобы геометрические фигуры заняли частное положение, необходимо выполнить преобразование чертежа. Существует несколько способов преобразования ортогонального чертежа:

Способ замены плоскостей проекций;

Способ дополнительного проецирования;

Способ плоскопараллельного движения;

Способ вращения вокруг проецирующей прямой;

Способ вращения вокруг прямой уровня.

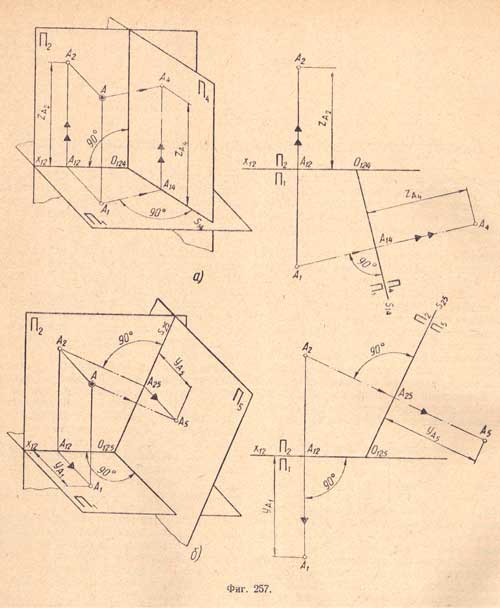
Рассмотрим первый способ - способ замены плоскостей проекций. Суть способа состоит во введении новой плоскости проекций П4 перпендикулярной одной из исходных плоскостей П1 либо П2 (отличную от П3). Заданные геометрические фигуры ортогонально проецируют на новую плоскость проекций.

Прямую пересечения новой плоскости с исходной принимают за новую ось проекции. Вращением вокруг новой оси совмещают новую плоскость проекций с плоскостью чертежа.

Можно сказать, что в этом случае фронтальную плоскость проекций П2 заменяем новой П4. При замене фронтальной плоскости проекций на новую остается неизменной аппликата z или высота данной точки А.

Алгоритм графических построений:

Провести ось проекций П1П4 пока произвольно. С полученной нами осью проекций П1П4 можно работать также, как и с привычной нам П1П2;

Провести новую линию проекционной связи из A1 перпендикулярную оси П1П4;

Отложить от точки пересечения линии проекционной связи с осью П1П4 высоту точки A, равную расстоянию от A2 до оси П1П2.

Можно ввести новую плоскость П4 перпендикулярную П2, или, можно сказать, заменить горизонтальную плоскость П1 на П4. В новой системе плоскостей П2 - П4 новой осью является П2П4.

При замене горизонтальной плоскости проекций на новую неизменной остается ордината y или глубина данной точки.

Алгоритм графических построений:

Провести ось проекций П2П4 пока произвольно.;

Провести новую линию проекционной связи из A2 перпендикулярную оси П2П4;

Отложить от точки пересечения линии проекционной связи с осью П2П4 высоту точки A, равную расстоянию от A1 до оси П1П2.

Для решения некоторых задач достаточно выполнить одну замену плоскостей проекций. Решение других задач могут потребовать выполнения двух замен и более. Мы можем вводить любое количество дополнительных плоскостей проекций. Причем они могут вводится не только таким образом, чтобы быть перпендикулярными к П1 и П2 и заменять их, но и для замены уже введенных дополнительных плоскостей проекций.