13. Плоское движение твёрдого тела. Закон движения.

Плоским движением твёрдого тела наз.такое движение,при котором все точки тела движутся параллельно какой-нибудь неподвижной(основной)плоскости. Если мы будем знать,как движется сечение твёрдого тела в плоскости ,то мы будем знать,как движутся точки объёмного тела по отношению к неподвижной плоскости,поэтому дальше мы будем изучать сечение движения плоскости.Выберем произвольную точку тела ; -ур-е движения твёрдого тела.

14. Плоское движение твёрдого тела. Скорости и ускорения точек тела.

Плоским движением твёрдого тела наз.такое движение,при котором все точки тела движутся параллельно какой-нибудь неподвижной(основной)плоскости. 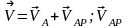наз вращательная скорость точки P вокруг полюса А.

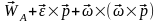;где

_{Ускорение полюса,} вращ-е ускорение точки рв её вращ-м движении вокруг точки А, центрострем-е ускор-е точки р в её вращ-м движ вокруг А.

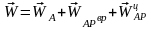
15.Плоское движение твёрдого тела. Мгновенный центр скоростей.

1)Мгнов. центр скоростей (обозн. I)- точка, скор-ть кот-ой в данный момент вр. =0. Она может или не телу, но должна быть неизменно с ним связана.

3)Пусть I-МЦС.

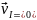
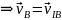
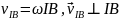. IB-мгновенный центр скоростей(РИСУНОК В КОНСП)

4) Если векторы лин-ых скор-тей 2ух различных точек тела парал-ны друг другу, и отрезок, соед-щий эти точки, не перпенд. вект-ам этих скор-ей, то перпенд-ры к этим вект-ам также парал-ны. Тогда говорят, что м.ц.с нах-ся в бесконечности. Если 2-е различные точки тела не парал-ны друг другу необх. провести из этих точек перпенд-ры к направлениям их скор-ей.Тогда в точке пересеч. этих перпенд-ов и будет нах-ся м.ц.с.

16. Cложное движение точки. Скорость точки. 1)Абсолютным движением наз-ся движение т. P относительно неподвижной системы координат. Относительным движением наз-ся движение т. P относительно тела S. Переносным движением наз-ся движение тела S координат относительно неподвижной системы координат. 2)Абсолютной скоростью на-ся скрость т. Р в её абсолютном движении. Относительной скоростью на-ся скрость т. Р в её относительном движении. Переносной скростью наз-ся скорость точки тела S c кот-й в данный момент совпадает т.Р

3)Т-а. Абсолютная скорость точки = геометрической сумме его относительной и переносной скоростей.

Док-во: Ax'y'z'- подвижная система координат, связанная с телом P

;

+

+ =

+ + = =

=

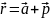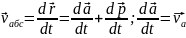
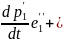
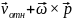
17. Сложное движение точки. Ускорение точки.

Пусть Oxyz – неподв. система корд., s- тело, движущееся по отношению к Oxyz, P – точка принадл. телу s. Переносным движением наз. движение тела s, по отношению к Оxyz. Относительным движением наз. движение т. P, по отношению к телу s. Абсолютным движением наз. движение т. Р по отношению к Oxyz. Абсолютным ускорением наз. ускорение т. Р в ее абсолютном движении. Относительным ускорением наз. ускорение т. Р в ее относительном движении. Переносным ускорением т. Р наз. ускорение той точки тела s, с которой в данный момент времени совпадает т. Р. Теорема (о сложении ускорений).В случае поступательного переносного движения абсолютное ускорение точки равно геометрической сумме ее относительного, переносного и кореолисова ускорения.Док-во: .

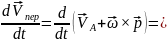
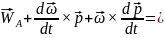
Следствие: в случае поступательного движения. Абс. Ускорение т. = геом. Сумме ее пер. и отн. ускорения.

18. Теорема об изменении количества движения материальной точки. 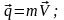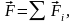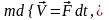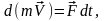Опр.к-вом движения точки массой m движущейся со скоростью V наз векторная величина ОПР.элементарным импульсом силы за элементарный промежуток времени dt наз векторная величина .ОПР.импульсом силы за промежуток времени t наз векторная величина т-ма об изменении количества движения в дифференциальной форме:элементарный импульс силы равен дифференциалу к-ва движения или .Д_Во: 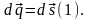конец д-ва.Проинтегрируем рав-во (1): 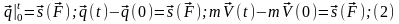.рав-во(2) выражает т-му об изменении движения в интегральной форме:изменение к-ва движения за некоторый промежуток времени=импульсу силы,действующей на точку за тот же промежуток времени.

19.Т-а об изменении кинет-й энергии матер-й очки

1)Кинетической энергией массы m, движущейся со скоростью 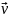наз-ся скалярная величина 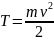.2) Элементарной работой силы на элементарном приращении 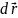наз-ся скалярную величину . Проекция на касательную вектора , умноженного на элементарную работу: 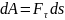. Работой силы на некотором перемещении наз-ся величина . 3)Дифференциал кинетической энергии точки= элементарной работе. 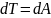. Док-во: ;

; = ; = ; (*)

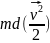Проитегрируем рав-во (*) 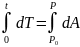; . 4)Т-а об изменении кинетической энергии в интегральной форме:Изменение кин-й энергии точки при некотором её перемещении = алгебраической сумме работ, действующих на точку на том же перемещении.

№19(20) Теорема об изменении кинетического момента материальной точки

Кинетическим моментом(или моментом кол-ва движ) т.Р массой m движ-ейся со скор. относит. полюса О наз-ся (РИСУНОК В КОНСП)

Теор.(об изм. кинет-го момента) Производная по времени от кинет-го момента точки относ-но некот-го неподвижного центра = сумме моментов всех сил, действующих на точку относит-но того же центра.

◄ ►

Теор(об изм.кин-го мом.относ оси) Производная по врем от кинет-го момента сист относит-но неподв оси = сумме моментов всех внешних сил относит-но этой оси.