Для этого:

1) В ячейки А3:А7 введите названия переменных и функций. В ячейку В3 введите значение 2.

2) В ячейки В4:АВ введите значение угла в градусах с шагом 15 с помощью автозаполнения

3) Для вычисления x в радианах в ячейку В5 введите формулу: =В4*ПИ( )/180 и скопируйте ее в ячейки С5:AB5 с помощью автозаполнения.

4) В ячейку В6 введите формулу: =SIN(B5) и скопируйте ее в ячейки С6:АВ6.

5) В ячейку В7 введите формулу: =Mysin(B5;$B$3) и скопируйте ее в ячейки С7:АВ7.

6) Далее постройте график на основе данных о вычислении синуса. Выделите ячейки А6:АВ6 и выполните команду: Вставка → График. Измените значения горизонтальной оси категорий. Для этого щелкните на названии горизонтальной оси левой кнопкой мыши и правой кнопкой вызовите контекстное меню. Далее выполните команду: Выбрать данные. В окне выбор источника данных в левом поле Элементы легенды (ряды) окна щелкните на названии функции SIN(x), а в правом поле Подписи горизонтальной оси (категории) щелкните на кнопке Изменить. Откроется диалоговое окно Подписи оси, далее выделите диапазон ячеек В5:АВ5 (значение угла в радианах). В результате в строке Диапазон подписей оси будет введен диапазон подписей: ='Mysin N=2'!$B$5:$AB$5, нажмите ОК. Аналогично проделайте для функции =Mysin (x, N).

7) Для того, чтобы изменить угол наклона подписей горизонтальной оси выполните в контекстном меню команду: Формат оси → Выравнивание → Другой угол → выберите свой угол поворота, например: −57 град.

8) В контекстном меню выберите команду: Шрифт и измените начертание шрифта на Times New Roman. В результате график примет вид как на рисунке 11.

Таблица 1:

i	1	2
s	x
q

Рис. 10. Вычисление синуса по слагаемым ряда, N=2.

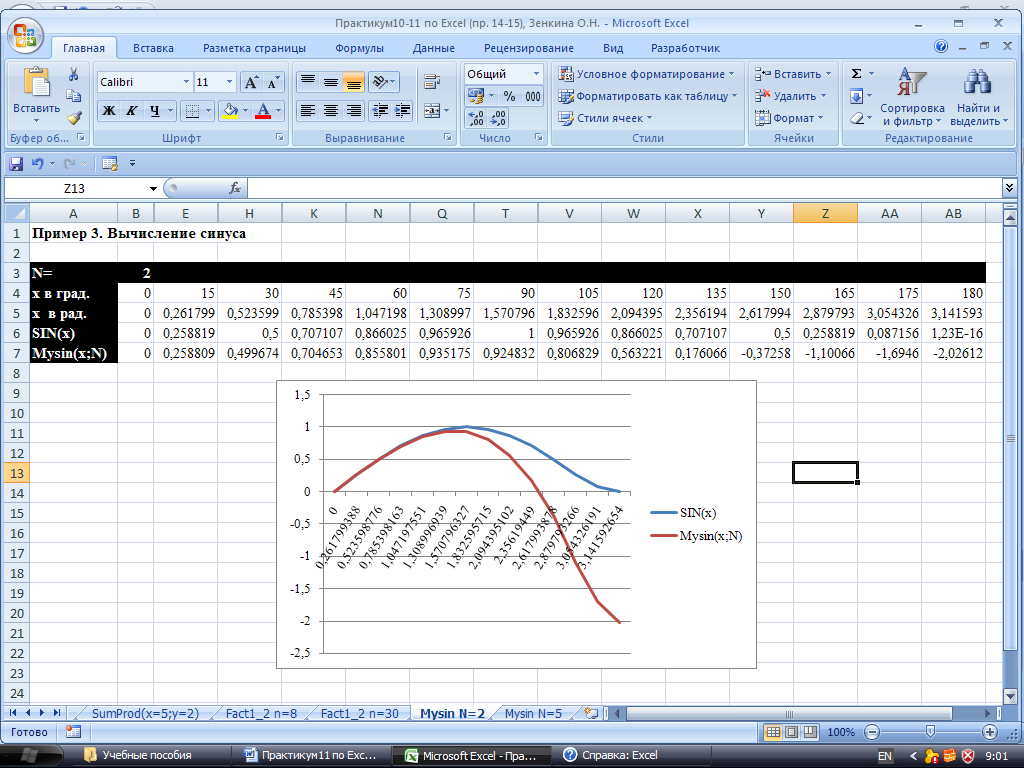
Рис. 11. Результат построения графиков для синуса и его приближенного значения, N=2.

Из построенных на рисунке 11 графиков видно, что для двух слагаемых ряда вычисленное на основе функции пользователя значение синуса близко к значению, вычисляемому на основе встроенной функции Excel SIN( ) только для небольших значений аргумента.

9) Ситуация существенно меняется, если увеличить число слагаемых в ряде, на основе которых вычисляется приближенное значение синуса. Вычислите приближенное значение синуса для N=5. Результат вычислений для 5 слагаемых ряда, см. на рис. 12:

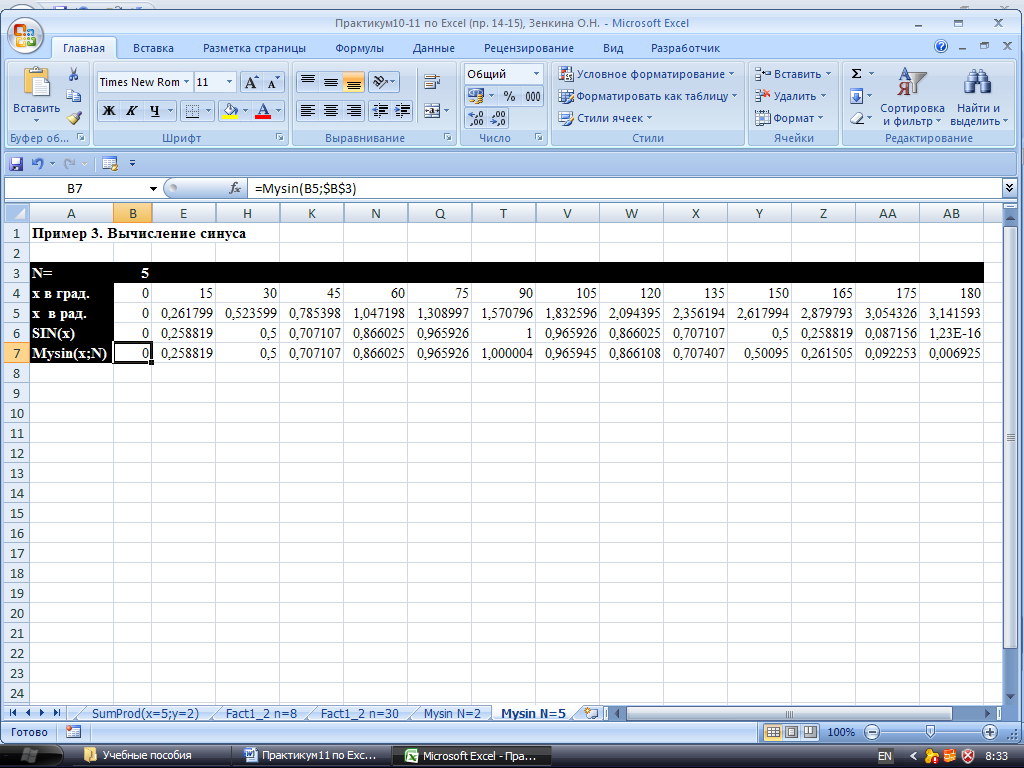
Рис. 12. Вычисление синуса по слагаемым ряда, N=5.

10) Постройте диаграмму с двумя графиками для случая, когда число слагаемых ряда N=5 (см. рис. 13). Измените внешний вид диаграммы с помощью команды контекстного меню: Формат ряда данных. Для этого щелкните левой кнопкой мыши на графике функции Mysin(x,N), далее в контекстном меню выберите: Формат ряда данных. На вкладке Параметры маркера выберите: Нет. На вкладке Цвет линии выберите: Сплошная линия: цвет красный. Закройте окно Формат ряда данных. В результате диаграмма примет вид как на рис. 13:

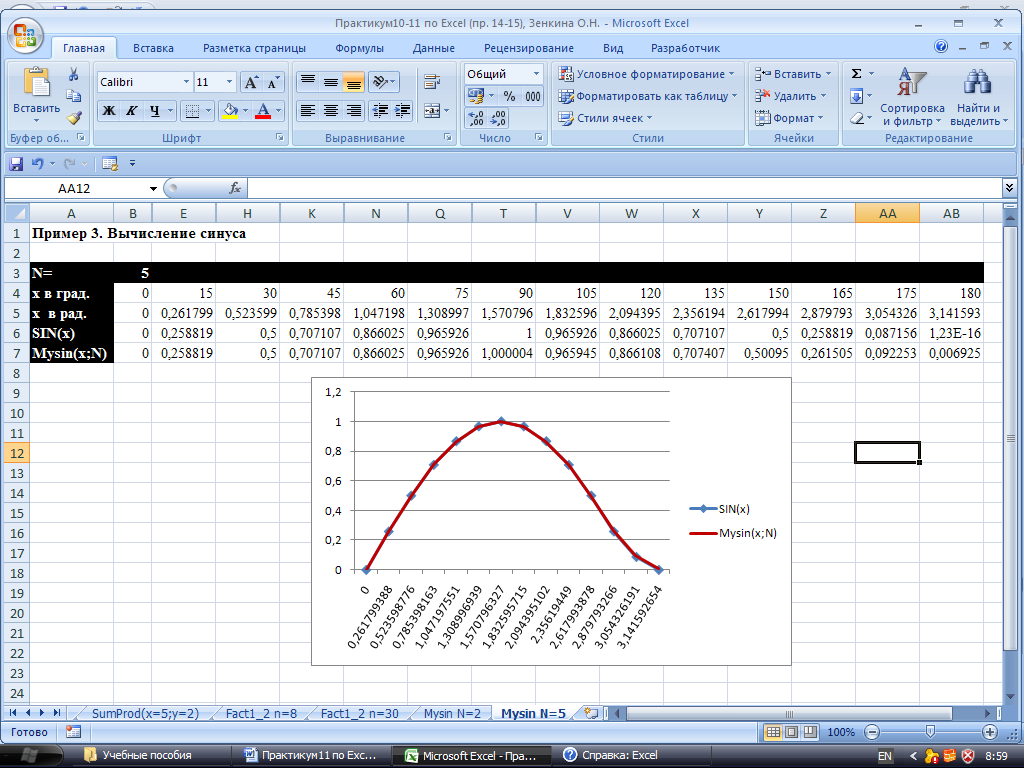
Рис. 13. Результат построения графиков для синуса и его приближенного значения, N=5.

Из рисунка 13 видно, что построенные на основе разных функций (встроенной функции Excel и пользовательской функции) графики совпадают (для различения графиков функций, график синуса помечен маркерами базовых точек).

Однако если расширить диапазон аргумента синуса различия станут более очевидными, т.к. чем больше аргумент синуса, тем больше слагаемых ряда нужно учесть для вычисления приемлемого значения. Тем не менее, какие бы значения ни принимал аргумент, с помощью созданной пользовательской функции можно находить его значения с любой точностью (в пределах возможности системы).

Пример 4.

Создание кусочно-гладкой функции.

Часто встречается такая ситуация, что приходится использовать функцию «сшитую» из нескольких фрагментов, каждый из которых является некой аналитической зависимостью. В этом случае использование Excel для создания специальной функции пользователя представляется достаточно эффективным.

В качестве примера рассмотрим процедуру создания функции, которая задается следующим образом: функция при x < 0, при и при . Программный код функции f( ) приведен в листинге 5:

Листинг 5. Программный код функции f ( )

Public Function f(x As Double) As Double

Select Case x

Case Is < 0

f = Exp(x)

Case Is > = 3

f = 4 * Exp(- sq(x – 3))

Case Else

f = sq (x – 1)

End Select

End Function

При определении функции f( ) использовалась функция пользователя sq ( ) для вычисления квадрата числа. Код этой простой функции приведен в листинге 6:

Листинг 6. Программный код функции sq ( )

Public Function sq(x As Double) As Double

sq = x*x

End Function

Для этого:

1) Введите как и в предыдущих примерах коды функций sq и f в окне редактора VBA в отдельных модулях. Проверьте ошибки с помощью команды: Debug → Compile VBAProject.

2) В окне Excel в ячейки А3 и А4 введите названия аргумента x и функции f(x)

3) В ячейки В3:ВТ3 введите значение аргумента с шагом 0,1 в интервале -2 < x < 5

4) В ячейку В4 введите формулу: =f(B3). Далее скопируйте её в ячейки С4:ВТ4. Результат вычислений пользовательской функции f(x) приведен на рис. 14.

Примечание 1: если после ввода кодов функций и отсутствия ошибок в них, в рабочем окне Excel при вызове функции пользователя f( ) возникает ошибка #ИМЯ закройте файл Excel и откройте снова, не забывая включить содержимое макросов, возможно вы забыли это сделать!

5) Выделите ячейки А4:ВТ4. Далее выполните команду: Вставка → График. Для изменения значений горизонтальной оси категорий см. п.6, пример 3.

6) В результате получится график как на рис. 15. Из графика, представленного на рис 15, отчетливо видно из каких фрагментов он состоит.

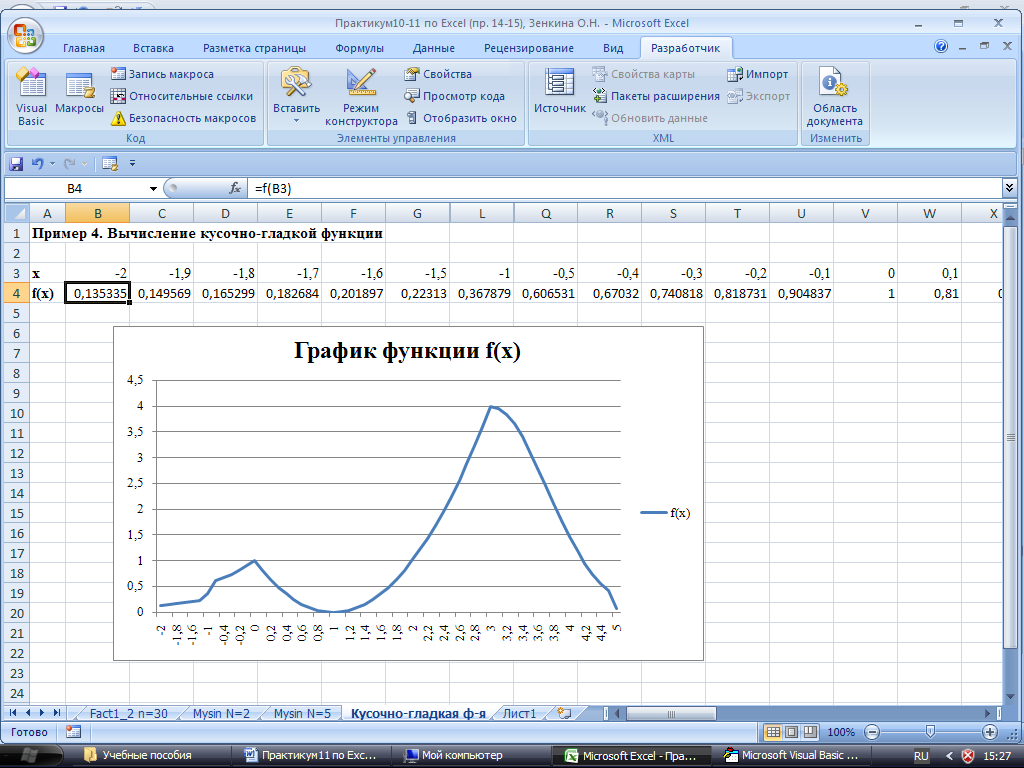
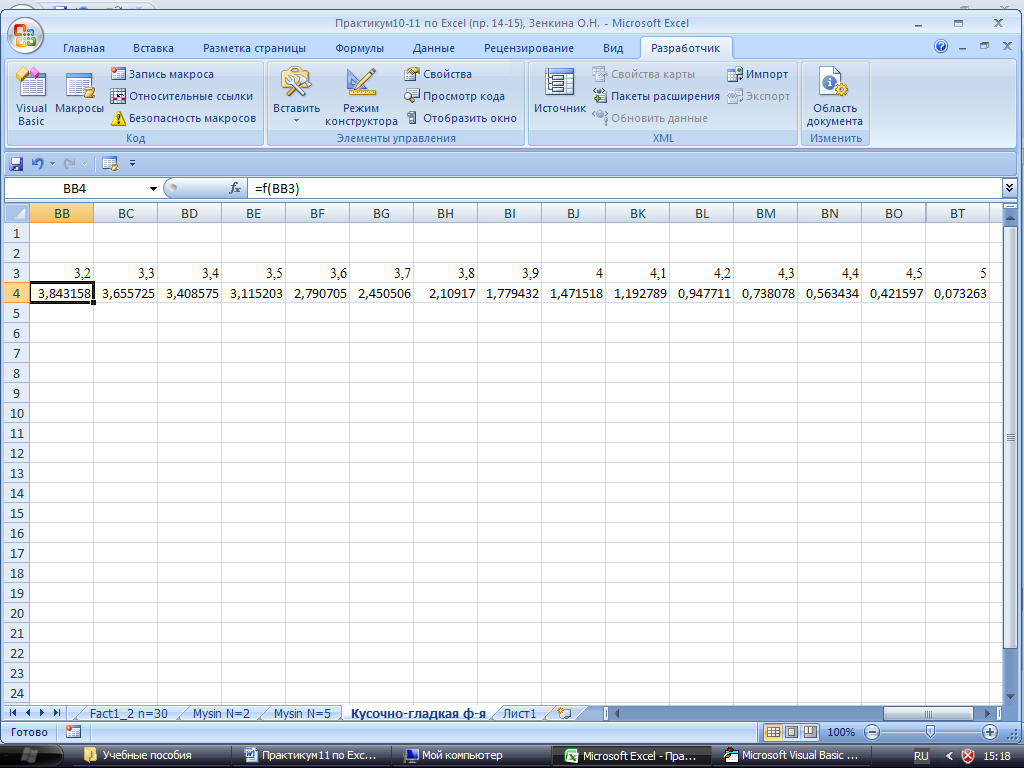
Рис. 14. Таблица данных для пользовательской функции f (x).

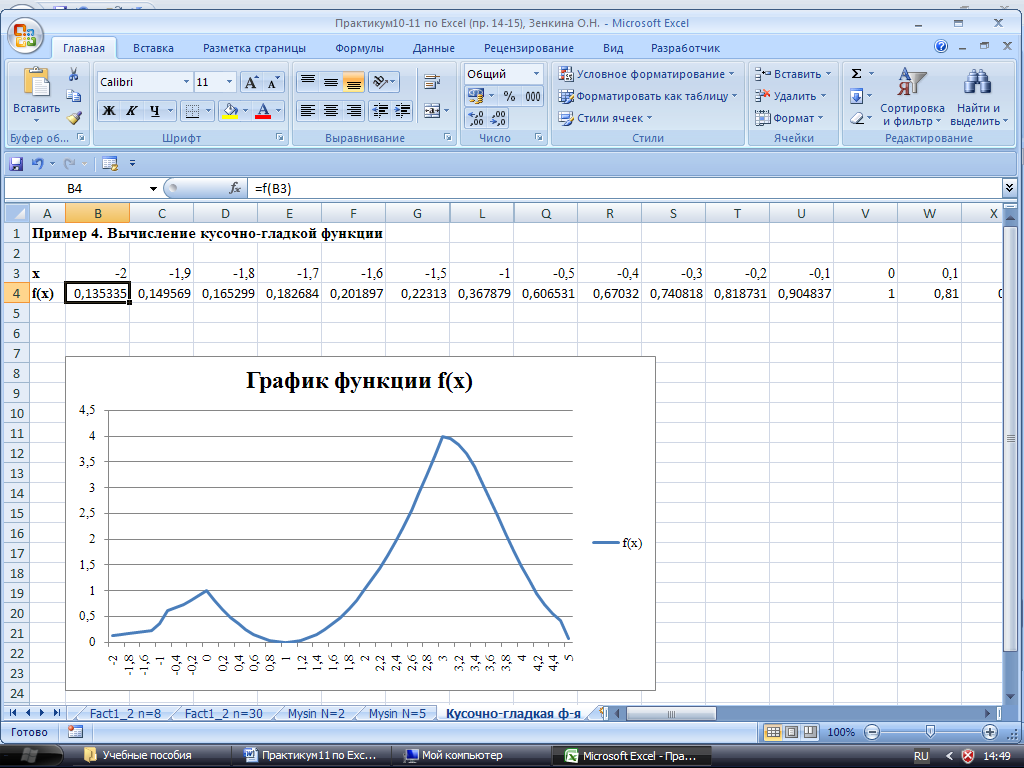
Рис. 15. Результат построения кусочно-гладкой функции.

Пример 5.

Вычисление числа Фибоначчи.

В работе № рассматривалось создание макроса для заполнения ячеек таблицы числами Фибоначчи. Однако для этих целей можно создать специальную функцию, которая по аргументу-номеру числа определяла бы его.

Функцию можно создать разными способами. Рассмотрим создание функции с помощью рекурсивного вызова.

Код функции Fibonacci ( ) приведен в листинге 7:

Листинг 7. Программный код функции Fibonacci ( )

Public Function Fibonacci (n As Integer) As Double

If n = 1 Or n = 2 Then

Fibonacci = 1

Else

Fibonacci = Fibonacci (n – 1) + Fibonacci (n – 2)

End If

End Function

Программный код выглядит достаточно компактно и прост в объяснении. Его основу составляет единственный условный оператор, в котором первым двум номерам в соответствие ставится единичное значение, а для вычисления чисел с большими порядковыми номерами рекурсивно вызывается сама функция.

Код функции Fibonacci2 ( ) приведен в листинге 8:

Листинг 8. Программный код функции Fibonacci2 ( )

Public Function Fibonacci2 (n As Integer) As Double

Dim a As Double

Dim b As Double

D im i As Integer

Select Case n

Case Is = 1

Fibonacci2 = 1

Case Is = 2

Fibonacci2 = 1

Case Is > 2

a = 1

b = 1

i = 2

Do

b = b + a

a = b – a

i = i +1

Loop Until i > = n

Fibonacci2 = b

Case Else

Fibonacci2 = 0

End Select

End Function

Рис. 16. Результат вычисления чисел Фибоначчи с помощью разных функций: Fibonacci и Fibonacci2.

Алгоритм, использованный при создании функции Fibonacci2 ( ) подразумевает непосредственное вычисление чисел ряда. Среди особенностей можно отметить, что в данном случае использован оператор цикла Do….Loop Until, в котором условие окончания цикла проверяется после окончания каждого цикла, а не в начале, как в операторе Do While….Loop.Кроме того, для проблемных значений аргумента функции (например, отрицательных), в качестве значения возвращается 0. Результат вычисления чисел Фибоначчи с помощью пользовательских функций представлен на рис. 16.

Из результатов, представленных на рис. 16 видно, что они идентичны. Сравнивая оба подхода, следует отметить, что хотя в подходе с использованием рекурсии программный код выглядит эффектнее, но эффективностью он не отличается. При вычислении значения функции для больших аргументов на выполнение кода с рекурсией уходит значительное время, что связано с существенной загрузкой ресурсов системы.