13В.- Понятие собственного числа и собственного вектора квадратной матрицы и их нахождение. Свойства неотрицательных матриц.

Число называется собственным числом квадратной матрицы А, если существует такой ненулевой столбец Х, такой ,что

АХ= Х.

Столбец Х называется собственным вектором матрицы А, соответствующим ее собственному числу .

Собственные числа матрицы А являются корнями уравнения , которое называется характеристическим уравнением матрицы А.

Свойства неотрицательных матриц

Матрица называется неотрицательной, если все ее элементы являются неотрицательными числами.

Для неотрицательных квадратных матриц справедлива следующая теорема.

Теорема

Неотрицательная матрица A имеет неотрицательное собственное число, которое обозначается _A, обладающее следующими свойствами:

7.Собственное число _A больше или равно модулей собственных чисел матрицы A.

8.Существует неотрицательный собственный вектор, соответствующий _A. Число _A называется числом Фробениуса (корнем Фробениуса).

Пусть сфера производства экономики разбита на n «чистых» отраслей, то есть каждая отрасль производит только один вид продукции, совместное производство исключается. Различные отрасли выпускают разные виды продукции.

Пусть для определенности число «чистых» отраслей равно 3.

Допустим, что по итоговым данным прошлого года составлен балансовый отчет по форме, приведенной в следующей таблице. Данная таблица называется таблицей межотраслевого баланса.

14В.-Таблица межотраслевого баланса. Понятие коэффициентов прямых затрат.

Таблица межотраслевого баланса

Отрасли	Промежуточный продукт			Конечный продукт	Валовой выпуск
	1 отрасль	2 отрасль	3 отрасль
1 отрасль	c11	c12	c13	y1	x1
2 отрасль	c21	c22	c23	y2	x2
3 отрасль	c31	c32	c33	y3	x3

В экономике конечный продукт называется конечной продукцией или конечным спросом, промежуточный продукт – промежуточным спросом.

Балансовый характер таблицы заключается в том, что для строк таблицы должны выполняться следующая система равенств:

Коэффициентом прямых затрат a_ij называется объем продукции i отрасли, который используется для производства единицы продукции отрасли j.Выскажем следующие предположения о коэффициентах прямых затрат:будем считать, что коэффициенты прямых затрат сохраняют свои значения в течение некоторого периода времени (года или нескольких лет);

• будем считать, что для производства продукции отрасли j в объеме x единиц, необходимо первой, второй и третьей отраслям произвести продукции в объемах a_1jx, a_2jx, a_3jx единиц.

Используя эти предположения, преобразуем систему равенств для строк таблицы межотраслевого баланса. В итоге приходим к системе линейных уравнений, которая и представляет модель Леонтьева.

15. Модель Леонтьева (из лекции)!!!!!

Пусть сфера производства экономики разбита на n «чистых» отраслей, то есть каждая отрасль производит только один вид продукции, совместное производство исключается. Различные отрасли выпускают разные виды продукции.

Пусть для определенности число «чистых» отраслей равно 3.

Д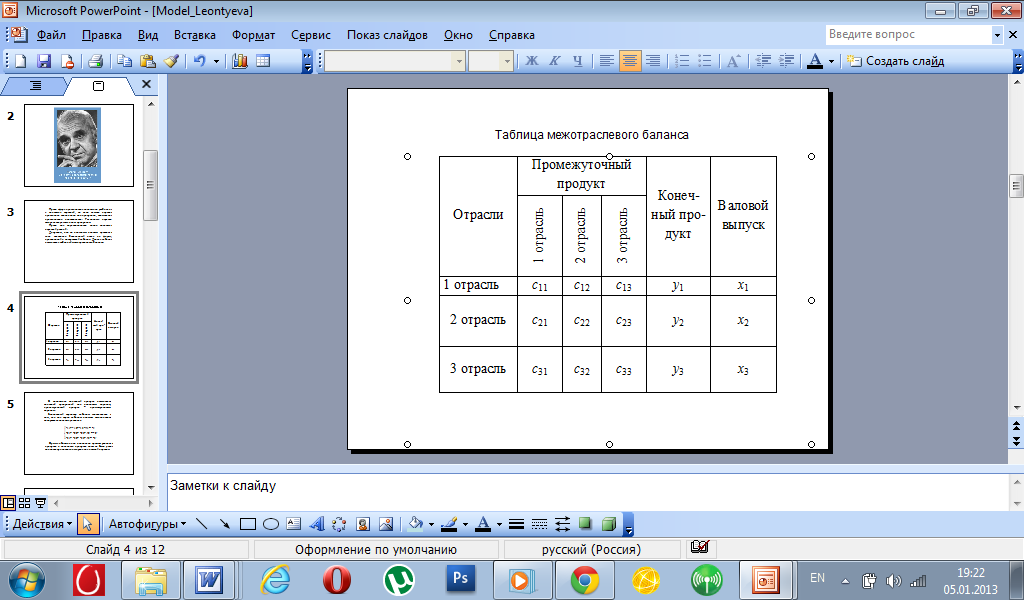 опустим, что по итоговым данным прошлого года составлен балансовый отчет по форме, приведенной в следующей таблице. Данная таблица называется таблицей межотраслевого баланса.

В экономике конечный продукт называется конечной продукцией или конечным спросом, промежуточный продукт – промежуточным спросом.

Балансовый характер таблицы заключается в том, что для строк таблицы должны выполняться следующая система равенств:

Коэффициентом прямых затрат a_ij называется объем продукции i отрасли, который используется для производства единицы продукции отрасли j.

Выскажем следующие предположения о коэффициентах прямых затрат:будем считать, что коэффициенты прямых затрат сохраняют свои значения в течение некоторого периода времени (года или нескольких лет);

будем считать, что для производства продукции отрасли j в объеме x единиц, необходимо первой, второй и третьей отраслям произвести продукции в объемах a_1jx, a_2jx, a_3jx единиц.

Используя эти предположения, преобразуем систему равенств для строк таблицы межотраслевого баланса. В итоге приходим к системе линейных уравнений, которая и представляет модель Леонтьева.

Итак, модель Леонтьева имеет следующий вид:

М одель Леонтьева можно записать и в матричном виде:

A – матрица коэффициентов прямых затрат;

Y – столбец объемов конечного продукта;

X - столбец валового выпуска продукции отраслей.