
- •1 Вопрос- Понятия модели, моделирования. Классификация экономико–математических моделей.
- •2.Понятие задачи на условный экстремум.
- •3. Метод множителей Лагранжа решения задачи на условный экстремум.
- •4.Отношение предпочтения.
- •5. Функция полезности.
- •9 Вопрос- Уравнение Слуцкого.
- •10 Вопрос - Понятие производственной функции. Неоклассическая производственная функция. Понятие производственной функции.
- •11В.-Модели поведения производителей.
- •Модель минимизации затрат при заданном объеме выпуска продукции
- •12В.- Модели взаимодействия потребителей и производителей: паутинообразная модель.
- •13В.- Понятие собственного числа и собственного вектора квадратной матрицы и их нахождение. Свойства неотрицательных матриц.
- •14В.-Таблица межотраслевого баланса. Понятие коэффициентов прямых затрат.
- •15. Модель Леонтьева (из лекции)!!!!!
- •16В.- Понятие продуктивности модели Леонтьева. Условия продуктивности.
- •17В.- Понятие коэффициентов полных затрат. Нахождение коэффициентов полных затрат.
- •18. Нахождение объемов валовой продукции отраслей. Коэффициенты полных затрат
- •19В.Обобщенная модель Леонтьева. Эффект замещения в обобщенной модели Леонтьева.
9 Вопрос- Уравнение Слуцкого.
Уравнение Слуцкого является основным уравнением в теории потребления. Оно отражает воздействие цены на спрос на эффект замещения и эффект дохода. С помощью уравнения Слуцкого можно классифицировать товары, анализировать их свойства и получать полезные для практики потребления выводы.
В уравнении Слуцкого рассматриваются изменения спроса при изменении цен и дохода. Предполагается незначительным изменение цен и дохода. Тогда изменение спроса при изменении цен и дохода можно определить с помощью частных производных.
Уравнение Слуцкого записывается в следующей математическом виде
![]()
Первое слагаемое в правой части описывает действие эффекта замены. Рассмотрим подробнее эффект замены. Цена на товар увеличилась на некоторую величину, увеличение цены компенсируется (заменяется) увеличением дохода, при этом полезность набора товаров остается на прежнем уровне. Эффект замены описывает изменение спроса, если увеличение цены компенсируется увеличением дохода.
Второе слагаемое со знаком минус – действие эффекта дохода, то есть как изменяется спрос при увеличении дохода.
В левой части записано результирующее воздействие на спрос, то есть как изменяется спрос при увеличении цены.
Используем уравнение Слуцкого для характеристики типов товаров
Типы товаров
Товар вида j называется нормальным, если
Товаром Гиффина, если
Среди покупателей с низким уровнем дохода рост цен на малоценные товары (картофель, хлеб) может вызвать повышение спроса на эти товары за счет отказа от покупок более ценных
Ценным, если
Малоценным, если
Д
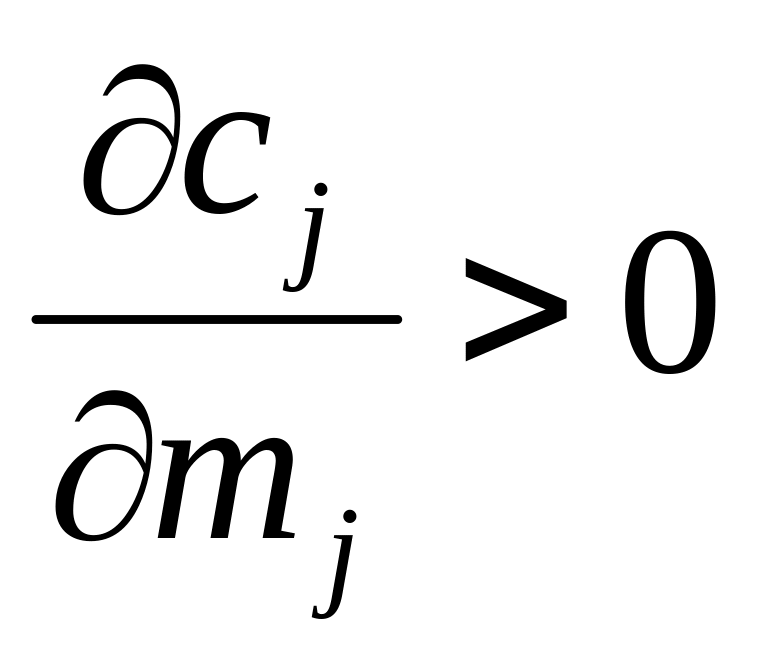 ва
товара I
и j
называются взаимозаменяемыми (например
животное и растительное масло), если
ва
товара I
и j
называются взаимозаменяемыми (например
животное и растительное масло), если
![]()
Взаимодополняемыми, если
В этом случае говорят, что товары I и j являются взаимодополняемыми.
Например, компенсируемое увеличение цены на бензин приводит к падению спроса на бензин и к падению спроса на автомобили. Бензин и автомобили являются взаимодополняемыми товарами
В общем случае каждый товар попадает в одну из следующих категорий:
Нормальный и ценный.
Нормальный и малоценный.
Товар Гиффина и малоценный.
10 Вопрос - Понятие производственной функции. Неоклассическая производственная функция. Понятие производственной функции.
При производстве продукции предприятия (производители) затрачивают различные ресурсы – вещественные блага и услуги (факторы производства), например труд и оборудование, и в результате выпускают разнообразную продукцию (результаты производства). Технологически эффективную производственную деятельность предприятия можно описать с помощью производственной функции.
Производственной функцией называется зависимость результата производства от затрат ресурсов.
Математически производственную функцию можно записать в следующем виде (для определенности число ресурсов равно двум):
![]()
Неоклассические производственные функции
Производственная функция называется неоклассической, если она дифференцируема при всех значениях переменных и удовлетворяет следующим условиям, поддающимся естественной экономической интерпретации:
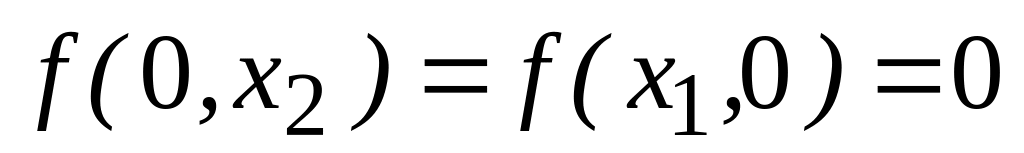 -
при отсутствии одного из ресурсов
производство невозможно;
-
при отсутствии одного из ресурсов
производство невозможно; -
с ростом объема одного из ресурсов, при
условии что объем другого ресурса
постоянен, выпуск растет;
-
с ростом объема одного из ресурсов, при
условии что объем другого ресурса
постоянен, выпуск растет;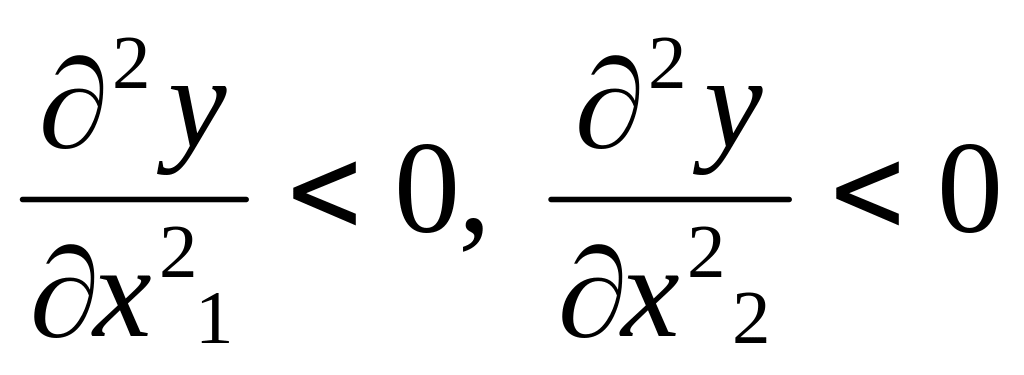 -
с увеличением ресурсов скорость роста
выпуска замедляется;
-
с увеличением ресурсов скорость роста
выпуска замедляется;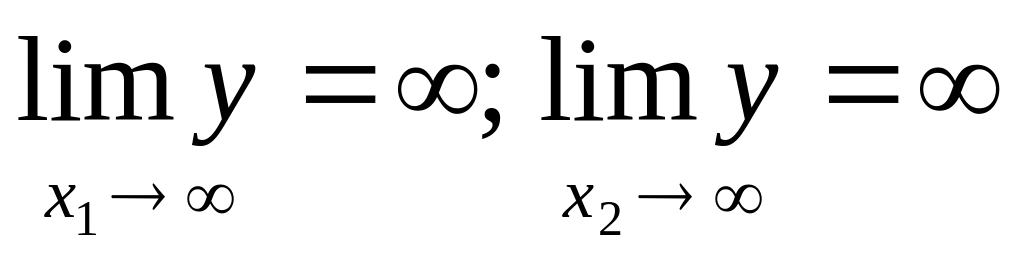 -
при неограниченном увеличении одного
из ресурсов выпуск неограниченно
растет.
-
при неограниченном увеличении одного
из ресурсов выпуск неограниченно
растет.
Примером неоклассической производственной функции является степенная функция следующего вида:
![]()
Функция Кобба - Дугласа
Частным случаем степенной неоклассической производственной функции является функция Кобба – Дугласа:
![]()
Свойства степенной неоклассической производственной функции
Показатели степеней степенной функции являются эластичностями выпуска продукции по ресурсам, то есть показывают приближенно на сколько процентов увеличивается объем выпуска продукции, если затраты ресурсов увеличились на один процент..
Рассмотрим во сколько раз увеличится объем выпуска продукции для степенной производственной функции (масштаб производственной функции) , если затраты ресурсов увеличиваются в k раз. Возможны следующие случаи:
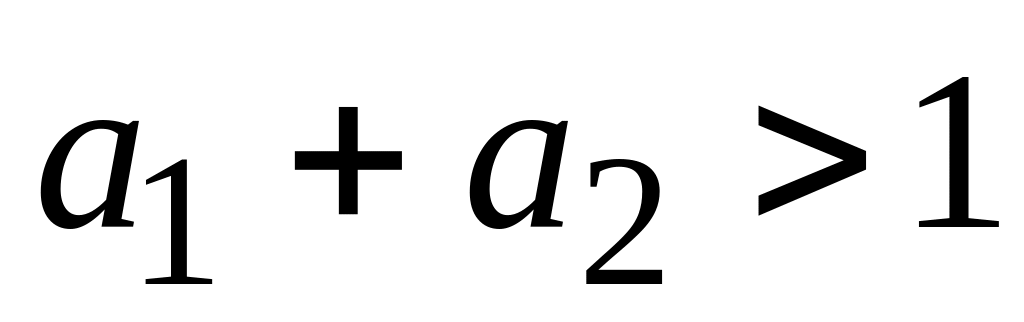 -
объем выпуска продукции увеличится
более чем в k
раз. Это
означает, что выпуск продукции растет
быстрее, чем затраты ресурсов. В этом
случае степенная функция описывает
интенсивный способ производства
продукции.
-
объем выпуска продукции увеличится
более чем в k
раз. Это
означает, что выпуск продукции растет
быстрее, чем затраты ресурсов. В этом
случае степенная функция описывает
интенсивный способ производства
продукции.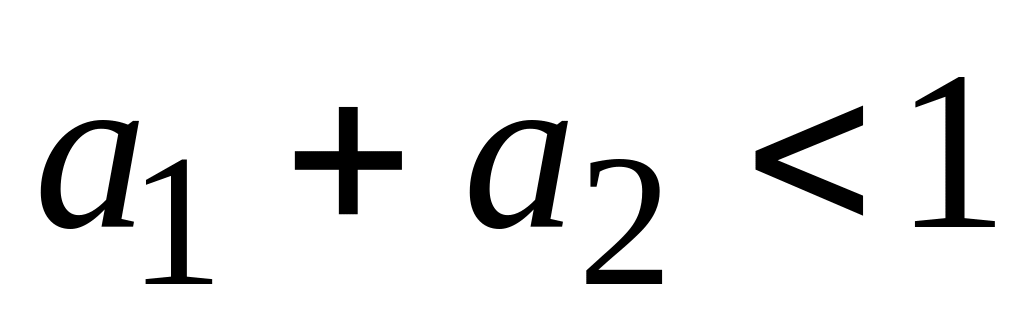 -
объем выпуска продукции увеличится
менее чем в k
раз. Это
означает, что выпуск продукции растет
медленнее, чем затраты ресурсов.
Производство продукции неэффективно.
-
объем выпуска продукции увеличится
менее чем в k
раз. Это
означает, что выпуск продукции растет
медленнее, чем затраты ресурсов.
Производство продукции неэффективно.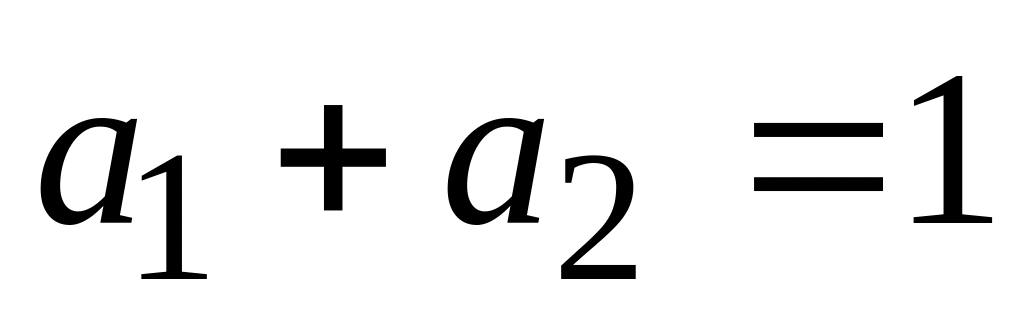 -
объем выпуска продукции увеличится в
k
раз, как
и затраты ресурсов. В этом случае можно
сказать, что продукция выпускается в
нормальном режиме. Производственная
функция Кобба – Дугласа описывает
нормальный режим выпуска продукции.
-
объем выпуска продукции увеличится в
k
раз, как
и затраты ресурсов. В этом случае можно
сказать, что продукция выпускается в
нормальном режиме. Производственная
функция Кобба – Дугласа описывает
нормальный режим выпуска продукции.
Примеры производственных функций
Производственные функции рассматриваются как на уровне экономики страны (макроуровень), так и на уровне отдельного предприятия (микроуровень).
В качестве ресурсов (факторов производства) на макроуровне наиболее часто рассматриваются накопленный труд в форме производственных фондов (капитал) K и настоящий (живой) труд L, а в качестве результата – валовой выпуск X (либо валовой внутренний продукт, либо национальный доход). Рассмотрим примеры производственных функций.
Зависимость валового выпуска Российской Федерации (млрд. руб.) от стоимости основных производственных фондов (млрд. руб.) и числа занятых в народном хозяйстве (млн. чел.) по данным за 1960 – 1994 гг. (все стоимостные показатели даны в сопоставимых ценах этого периода) имеет следующий вид:
![]()
Производственные функции можно построить и для отдельных предприятий. В США под руководством Э. Хеди были проведены исследования по определению производственных функций в земледелии и животноводстве, а также исследования экономики отдельных ферм.
В качестве примера приведем производственную функцию, характеризующую эффективность влияния азотных (x1) и фосфорных удобрений (x2) на урожайность кукурузы (y) на суглинках (значения показателей округлены до 0,1):
![]()
