4.Отношение предпочтения.

Рассмотрим множество наборов товаров, которые может приобрести потребитель за определенный срок при заданных ценах на товары и доходы потребителя за тот же срок.

Такой набор может включать один или несколько предметов потребления. Например, он может содержать различные продукты питания, одежду и топливо, которое потребителю покупает каждый месяц. Пусть набор включает два вида товаров.

Математически набор представляет собой вектор, координаты которого являются объемами потребления товаров. Также набор товаров можно представить в виде точки на координатной плоскости. 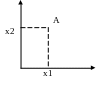где х1-объем потребления 1го товара, х2-объем потребления 2го товара.

Предположим, что на множестве наборов товаров выполнены следующие требования:

Требования полноты.

Либо набор х потребителя предпочтительнее набора у, либо набор х для потребителя менее предпочтителен, чем набор товаров у, либо для потребителя оба набора абсолютно одинаковой степенью предпочтения. Вместо слова «предпочтительнее» в математике используют символ , т.е. , а для одинаковой степени предпочтения х (волна) у.

Требования транзитивности.

Если набор х предпочтительнее набора у, а набор у предпочтительнее набора z, то набор х предпочтительнее набора z.

Требования рефлексивности

Набор х не хуже самого себя. Выполнение этих товаров математически означает, что на этом множестве введено отношение предпочтения.

Отношение предпочтения при определенных условиях, которые выполняются на практике, можно представить в виде функции полезности.

5. Функция полезности.

Введение ф-ции полезности позволяет заменить отношение предпочтения привычными отношениями между числами: больше, меньше, равно, т е из x y следует u(x)>u(y).

В теории потребления предполагается, что ф-я полезности обладает след. св-ми:

1. с ростом объема потребления i-го товара, при условии, что объемы др. товаров неизменны, полезность растет: >0

2. с ростом объема потребления i-го товара, при условии, что объемы др. товаров неизменны, темп роста (скорость роста) полезности замедляется (закон убывающей предельной полезности или закон Госсена): <0

6в-Понятие предельной полезности и предельной нормы замещения в теории потребления.

Предельная полезность

Основными понятиями теории потребления является предельная полезность и предельная норма замещения.

Пусть набор состоит из двух товаров или услуг:

Предельная полезность первого товара показывает на сколько максимально увеличится значение функции полезности, если объем потребления первого товара увеличился на малую единицу, а объем второго товара не изменился. Аналогично находится предельная полезность второго товара.

Математически предельная полезность первого товара равна значению частной производной на этом наборе. Для нахождения предельной полезности первого товара необходимо найти частную производную и в выражение подставить объемы потребления товаров. Полученное число и является предельной полезностью первого товара на данном наборе.

Предельная норма замещения

Предельная норма замещения первого товара вторым показывает, на сколько максимально, можно увеличить объем потребления второго товара при уменьшении объема потребления первого товара на малую единицу ,чтобы значение функции полезности не изменилось.

Рассмотрим множество наборов товаров , имеющих одинаковую полезность. Математически предельная норма замещения первого товара вторым товаром n равна отношению предельных полезностей первого и второго товара:

Определим предельную полезность каждого товара в оптимальной точке. Имеем:

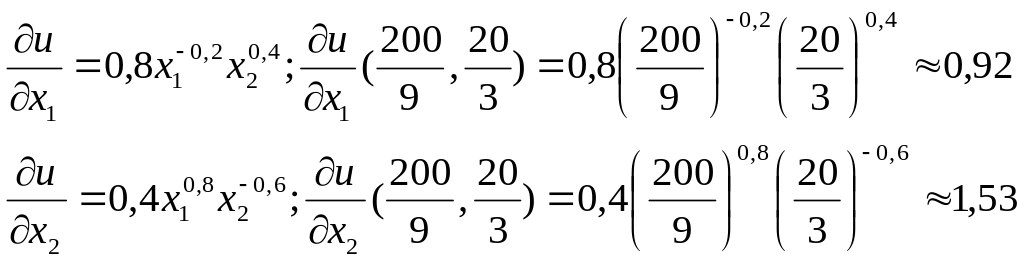
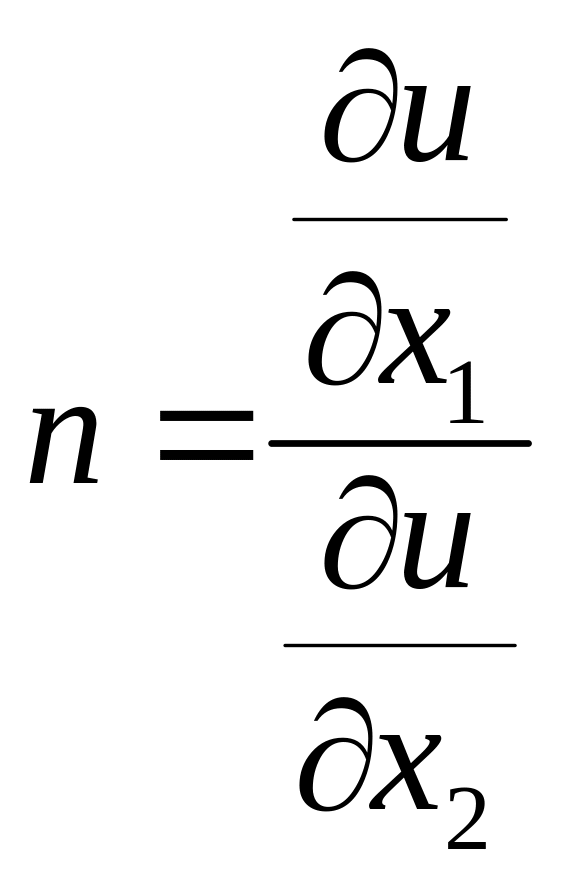
Определим предельную норму замещения первого товара вторым товаром:

В оптимальной точке предельная норма замещения первого товара вторым товаром равна отношению цен на товары.

7в.- Модель поведения потребителя. Понятие функции спроса.

Бюджетным множеством называется множество наборов товаров и услуг, который может приобрести потребитель. В теории потребления предполагается, что потребитель выбирает набор благ так, чтобы максимизировать полезность. Соответственно набор товаров называется оптимальным набором или оптимальным планом поребления. Оптимальный набор товаров должен удовлетворять следующим двум условиям:

4. он должен принадлежать бюджетному множеству

5. на этом наборе функция должна принимать наибольшее значение.

Математическая модель нахождения оптимального набора из двух товаров имеет следующий вид:

где р1 – цена 1го товара; р2 – цена 2го товара; m – доход потребителя; х1- объем потребления 1го товара; х2 – объем потребления 2го товара

Данная математическая модель называется моделью поведения потребителя

Можно доказать, что на оптимальном наборе бюджетное ограничение является равенством.

Используя модель поведения потребителя можно найти функцию спроса на товар.

Функция спроса в рыночном механизме является определяющей, ибо именно она заставляет производство выпускать необходимые населению товары, улучшать их качество и ассортимент.

Функцией спроса на товары называется математическая зависимость оптимального объема потребления товара от дохода и цен.

8.Понятие эластичности. Эластичность спроса по доходу и цене.

Эластичность спроса по доходу

Эластичность спроса по доходу представляет процентное увеличение спроса на товар, если величина дохода увеличилась на один процент.

Товар называют товаром с неэластичным спросом по доходу, если эластичность меньше 1; с эластичным спросом по доходу, если эластичность больше 1.

Товар называют товаром с нейтральным (безразличным или единичным) спросом по доходу, если эластичность равна 1.

Эластичность спроса по цене

Эластичность спроса по доходу представляет процентное уменьшение спроса на товар, если цена товара уменьшилась на один процент.

Товар называют товаром с неэластичным спросом по цене, если эластичность больше -1; с эластичным спросом по цене, если эластичность меньше -1.

Товар называют товаром с нейтральным (безразличным или единичным) спросом по цене, если эластичность равна -1.

Рассмотрим пример нахождения эластичности спроса по доходу и цене.

Функция спроса на товар имеет вид: y(m;p)=2m/3p₁

Найти эластичность спроса по доходу и цене.

Для расчета эластичности используют формулу!!!!!

Определим эластичность спроса по доходу:

При увеличении дохода на 1%, спрос увеличивается на 1%

Определим эластичность спроса по цене:

Функция полезности Стоуна

Реально эластичности спроса по доходу и цене не являются постоянными.

Для того чтобы устранить этот недостаток английский экономист Стоун предложил ввести следующую функцию полезности, которая для набора, состоящего из двух продуктов, имеет следующий вид:

Иначе функцию полезности Стоуна записывают в логарифмическом виде:

, где b₁>0, b₂>0, x₁>a₁, x₂>a₂