2.Понятие задачи на условный экстремум.

Задача на условный экстремум в простейшем виде записывается след. образом:

g(x₁;x₂)=0

f(x₁;x₂) min (max)

ограничения записываются в виде уравнений. Ограничения называются иначе уравнениями связи.

Говорят, что в т.М₀(x⁰₁;x⁰₂), которая удовлетворяет уравнению связи, целевая ф-я имеет условный локальный min, если для всех т.М₀(x₁;x₂), близких т.М₀, справедливо следующее неравенство: f(x₁;x₂) f(x⁰₁;x⁰₂). т.М₀ – т. условного локального min.

Определение условного локального max формулируется аналогично, только необходимо поменять знак неравенства на противоположный.

Т. условного локального min или max наз-ся т. условного локального экстремума.

Допустимая т. x^*(x^*₁;x^*₂) наз-ся оптимальным решением задачи на условный экстремум, если в этой т. целевая ф-ция принимает наим (наиб) значения. Оптимальное решение является т. условного локального экстремума. Обратное утверждение неверно.

В эконом-х задачах обычно т. условного локального экстремума явл-ся также и оптимальным решением задачи на условный экстремум.

3. Метод множителей Лагранжа решения задачи на условный экстремум.

1. Понятие задачи на условный экстремум. Запись задачи в простейшем виде.

Задачи на условный экстремум ограничения записываются в виде уравнения.

Ограничения задачи на условный экстремум называются иначе уравнениями связи.

Функция, достигающая наименьшее или наибольшее значение называется целевой функцией.

Пример: Найти на окружности точку, наименее удаленную от т.М

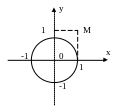
Обозначим координаты искомой точки через х и у

Прямоугольник с наибольшей площадью.

Стороны прямоугольника х и у

Тогда

Уточним понятие условного экстремума и рассмотрим методы его отыскания

Определение: Говорят, что в т.М , которая удовлетворяет связи целевой функции имеет условный локальный минимум, если для всех точек справедливо следующее неравенство:

Точка М называется точкой условного локального минимума.

Определение условного локального максимума формируется аналогично, только необходимо поменять знак на противоположный.

Точки условного локального минимума или максимума называются точками условного локального экстремума

Допустимая точка называется оптимальным решением задания на условный экстремум, если в этой точке целевая функция принимает наименьшее значение. Оптимальное решение является точкой условного локального экстремума.

В экономических задачах обычно точки условного локального экстремума являются также и оптимальным решением задачи на условный экстремум.

Лагранж – французский математик, предложил метод нахождения точек условного локального экстремума, который называется методом множителей Лагранжа.

Рассмотрим алгоритм этого метода для простейшей задачи на условный экстремум:

1). Записываем функцию Лагранжа. Переменная - называется множителем Лагранжа.

2). Находим частные производные первого порядка функции Лагранжа по переменным и приравниваем полученные выражения частных производных к 0.

(1)

3). Решаем эту систему относительно переменных . В результате будут найдены все возможные точки , которые могут оказаться точками условного локального экстремума.

Существует функция, в которой целевая функция принимает наменьшие или наибольшие значения. Эта точка является точкой условного локального экстремума и является решением системы уравнений.

Поэтому для нахождения оптимального решения необходимо выполнить следующие действия:

1. Необходимо найти значения целевой функции в найденных точках , которые являются решениями системы (1).

2. Выбрать среди найденных чисел наим. (наиб.) число.

3. Точка, которая соответствует наиб. или наим. значению целевой функции и будут являться оптимальным решением задачи на условный экстремум.