1 Вопрос- Понятия модели, моделирования. Классификация экономико–математиче­ских моделей.

Описание объекта называются моделью, а процесс построения модели называется моделированием.

Экономико–математической моделью называется описание различных экономических объектов на языке математики.

По величине изучаемого экономического объекта экономико-математические модели можно разделить на микроэкономические и макроэкономические.

Макроэкономические модели описывают экономику государства как единое целое. В рамках макроэкономических моделей изучаются проблемы общественного воспроизводства валового национального продукта и валового внутреннего продукта, национального дохода, влияния инновационных факторов на экономический рост. Рассматриваются вопросы оптимизации накопления и инвестирования, структурной мобильности экономики в условиях научно-технического прогресса, динамики общего уровня цен, инфляции, занятости, безработицы и многие другие вопросы.

Примерами макроэкономических моделей являются макроэкономические производственные функции, балансовые модели.

Микроэкономические модели описывают взаимодействие отдельных составляющих экономики, либо хозяйственное поведение таких составляющих. К составляющим экономики относятся потребители (домашние хозяйства) и производственные фирмы (производители).

Примерами микроэкономических моделей являются микроэкономические производственные функции, модель поведения потребителя, модели производственной фирмы в условиях совершенной и несовершенной конкуренции, модели взаимодействия потребителей и производителей.

По характеру зависимости от времени экономико-математические модели делят на статические и динамические.

Статическая модель – это модель, в которой значения всех параметров не зависят от времени.

Динамическая модель – модель, в которой параметры изменяются с течением времени.

Рассмотрим экономические понятия, которые используются в экономико– математических моделях.

Основная цель экономики – обеспечение общества предметами потребления. Экономика состоит из двух частей: производственной и финансово-кредитной.

Производственную часть экономики образуют производственные предприятия и фирмы.

Совокупность предприятий и фирм, занимающихся одним видом материального производства, образуют различные отрасли: промышленность, сельское хозяйство, строительство, транспорт и т.д.

В результаты функционирования производственной сферы экономики создается валовой внутренний продукт (ВВП) или конечный продукт.

В процессе создания ВВП производственная сфера производит и вновь потребляет промежуточный продукт. Промежуточный продукт – это предметы труда, использованные для производственного потребления.

Суммарная стоимость валового внутреннего продукта и промежуточного продукта образует валовой выпуск.

Для производства продукции используются различные ресурсы: природные ресурсы, средства производства, рабочая сила.

Средства производства, которые в течение длительного времени обслуживают процесс производства, образуют основные производственные фонды.

Финансово-кредитную часть экономики образуют государственные и коммерческие банки, их филиалы, страховые общества, бухгалтерские службы различных предприятий.

Финансово-кредитная часть экономики обеспечивает стабильный и справедливый обмен товарами и услугами, создает финансовые условия для развития производства. Деньги и другие ценными бумаги являются финансовыми ресурсами, которые используются для решения этих задач

Рассмотрим пример построения экономико-математической модели.

Имеем следующую экономическую задачу.

Производственная фирма выпускает один вид продукции. Для производства продукции используются два вида ресурсов – сырьё и рабочая сила. Зависимость валового выпуска продукции от затрат сырья и труда можно с высокой точностью описать следующей зависимостью:

где

y – валовой выпуск, тонн;

x₁ – затраты сырья, тонн;

x₂ – затраты труда, человеко-часы.

На закупку сырья и оплату труда предприятие может выделить 150000 ден. ед. Стоимость 1 тонны сырья равна 5 ден. ед., стоимость одного человека-часа равна 12 ден. ед. Какими должны быть затраты ресурсов, чтобы валовой выпуск продукции был максимальным?

Составим экономико-математическую модель задачи.

Составление модели можно разбить на ряд этапов:

1. Ввод переменных.

2. Запись ограничений на переменные.

3. Вводим целевую функцию, если необходимо найти наибольшее или наименьшее значения экономического показателя. Целевая функция зависит от выбранных переменных и выражает условие оптимальности.

Экономико-математическая модель задачи имеет следующий вид:

В итоге получаем следующую математическую задачу: найти наибольшее значение функции , если значения переменных удовлетворяют заданной системе ограничений.

Значения переменных, которые являются решением данной задачи, называются оптимальным решением.

Можно показать, что на оптимальном решении первое ограничение является равенством:

Выразим переменную x₂ через переменную x₁:

.

Подставим в целевую функция вместо переменной x₂ полученное выражение:

.

Так как переменная x₂ принимает неотрицательные значения, то переменная x₁ изменяется в пределах от 0 до 3000.

В итоге получаем следующую математическую задачу: найти наибольшее значение функции на отрезке [0; 3000].

Решим данную задачу. Найдем точки, в которых производная функции обращается в нуль.

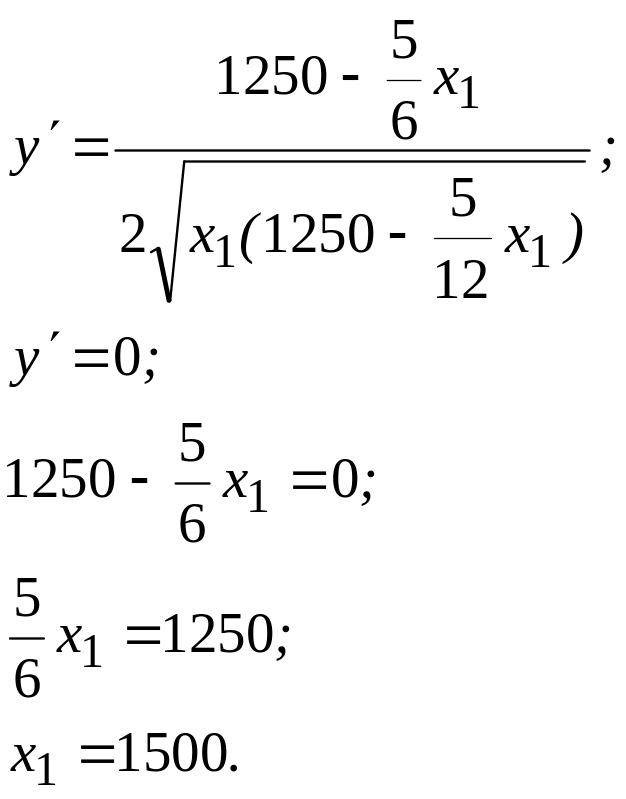
Так как на концах отрезка значения функции равны нулю, то значение переменной x₁, равное 1500, доставляет функции наибольшее значение.

Найдем значение переменной x₂:

Подведем итог.

Оптимальные затраты ресурсов следующие: затраты сырья 1500 тонн, затраты труда 625 человеко-часов.